Learn Java Deeply and Simply--HashMap

1. What is a hash table

Before discussing hash tables, let's take a look at the performance of other data structures in performing basic operations such as adding, finding, and so on.

Array: A continuous storage unit is used to store data.For a given subscript lookup, the time complexity is O(1); for a given value lookup, the array needs to be traversed, one by one, compared to a given keyword and array element, and the time complexity is O(n); of course, for an ordered array, the lookup complexity can be increased to O(logn) by using binary lookup, interpolation lookup, Fibonacci lookup, and so on; for a general insert-delete operationWork, involving the movement of array elements, with an average complexity of O(n)

Linear chain table: For addition, deletion and other operations of the chain table (after finding the specified operation location), only the references between the nodes need to be processed, the time complexity is O(1), and the lookup operation needs to be compared one by one through the chain table, the complexity is O(n)

Binary Tree: A relatively balanced ordered binary tree is inserted, searched, deleted, etc. with an average complexity of O(logn).

Hash table: Compared to the above several data structures, adding, deleting, finding operations in the hash table have very high performance. Without considering hash conflicts (we will discuss the situation of hash conflicts later), only one positioning is needed and the time complexity is O(1). Next, let's see how the hash table achieves a stunning constant order O(1).

As we know, there are only two physical storage structures for data structures: sequential storage and chained storage (stack, queue, tree, graph, etc.) which are abstracted from logical structure and mapped to memory, as well as the two physical organization forms. As mentioned above, when you look for an element in an array based on the subscript, you can do this at one time, and a hash table is usedIn this way, the backbone of a hash table is an array.

For example, if we want to add or find an element, we can do this by mapping the keywords of the current element to a position in the array through a function, and by positioning the array subscript once.
　　
This function can be simply described as: storage location= f (keyword). This function f is generally called a hash function. The design of this function will directly affect the quality of the hash table.For example, if we want to insert in a hash table:
The insertion process is illustrated below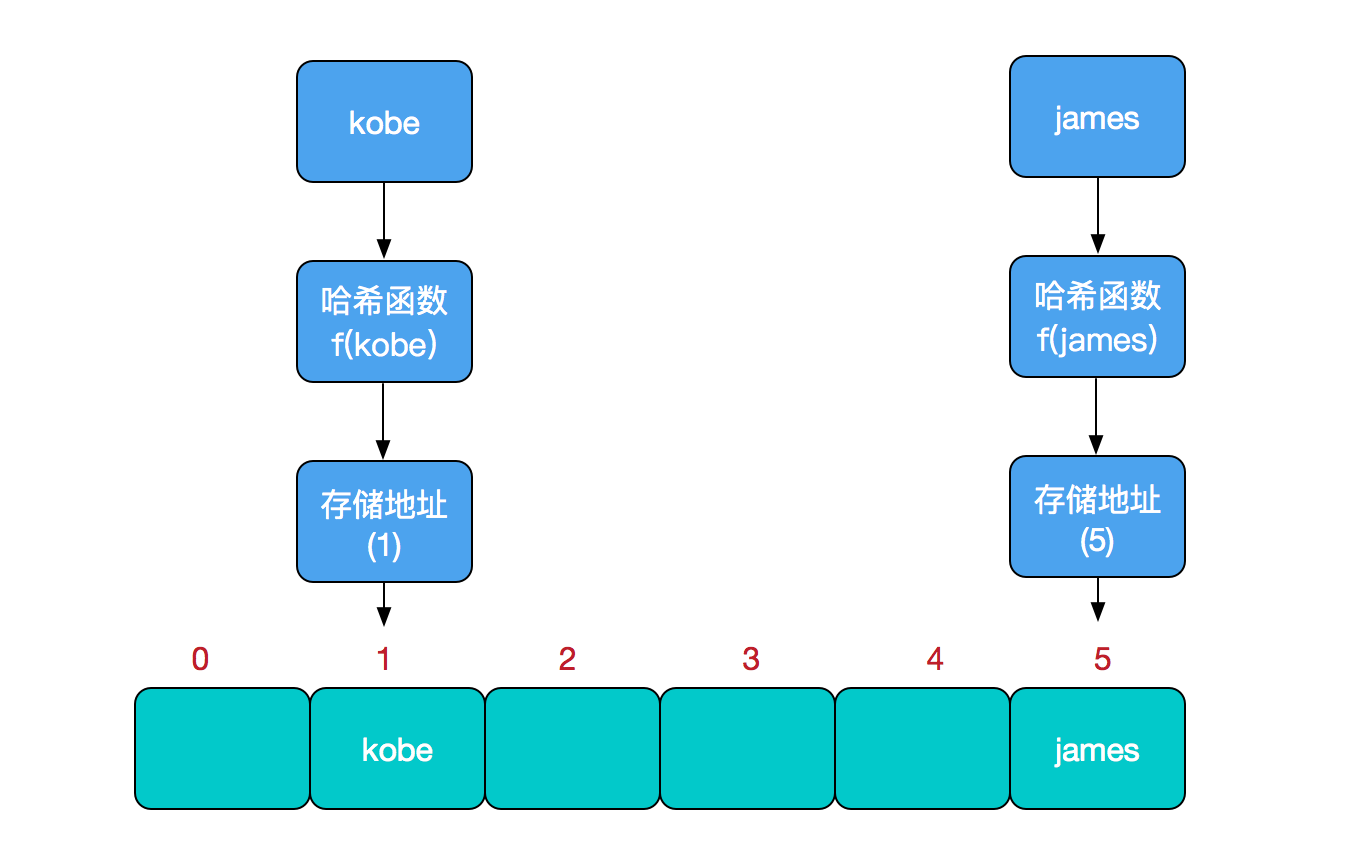

The same is true for a lookup operation, which first calculates the actual storage address through a hash function and then takes it out of the array.

Hash Collisions

However, everything is not perfect. What if two different elements have the same actual storage address from the hash function?That is, when we hash an element, get a storage address, and insert it, we find that it has been occupied by other elements. In fact, this is called a hash conflict, also known as a hash collision.As mentioned earlier, the design of a hash function is critical, and a good hash function ensures that calculations are as simple as possible and that hash addresses are evenly distributed. However, it is important to be clear that an array is a continuous fixed-length memory space, and that no good hash function can guarantee that the resulting storage addresses will never conflict.So how can hash conflicts be resolved?Hash conflicts can be resolved in a variety of ways: open addressing (where a conflict occurs and you continue to find the next unoccupied storage address), hash function, and chain address, whereas HashMap uses chain address, which is an array + Chain table.

2. Implementation principle of HashMap

The backbone of HashMap is an Entry array.Entry is the basic building block of HashMap, and each Entry contains a key-value pair.(Map is actually a collection of mapping relationships between two objects)

//The trunk array of HashMap, you can see is an Entry array, the initial value is an empty array {}, the length of the trunk array must be a power of 2.
//As to why this is done, a detailed analysis will follow.
transient Entry<K,V>[] table = (Entry<K,V>[]) EMPTY_TABLE;

Entry is a static internal class in HashMap.The code is as follows

    static class Entry<K,V> implements Map.Entry<K,V> {
        final K key;
        V value;
        Entry<K,V> next;//Stores references to the next Entry, single-chain table structure
        int hash;//The hash operation on the hashcode value of the key stores the value in Entry to avoid duplicate calculation

        /**
         * Creates new entry.
         */
        Entry(int h, K k, V v, Entry<K,V> n) {
            value = v;
            next = n;
            key = k;
            hash = h;
        } 

So the overall structure of HashMap is as follows: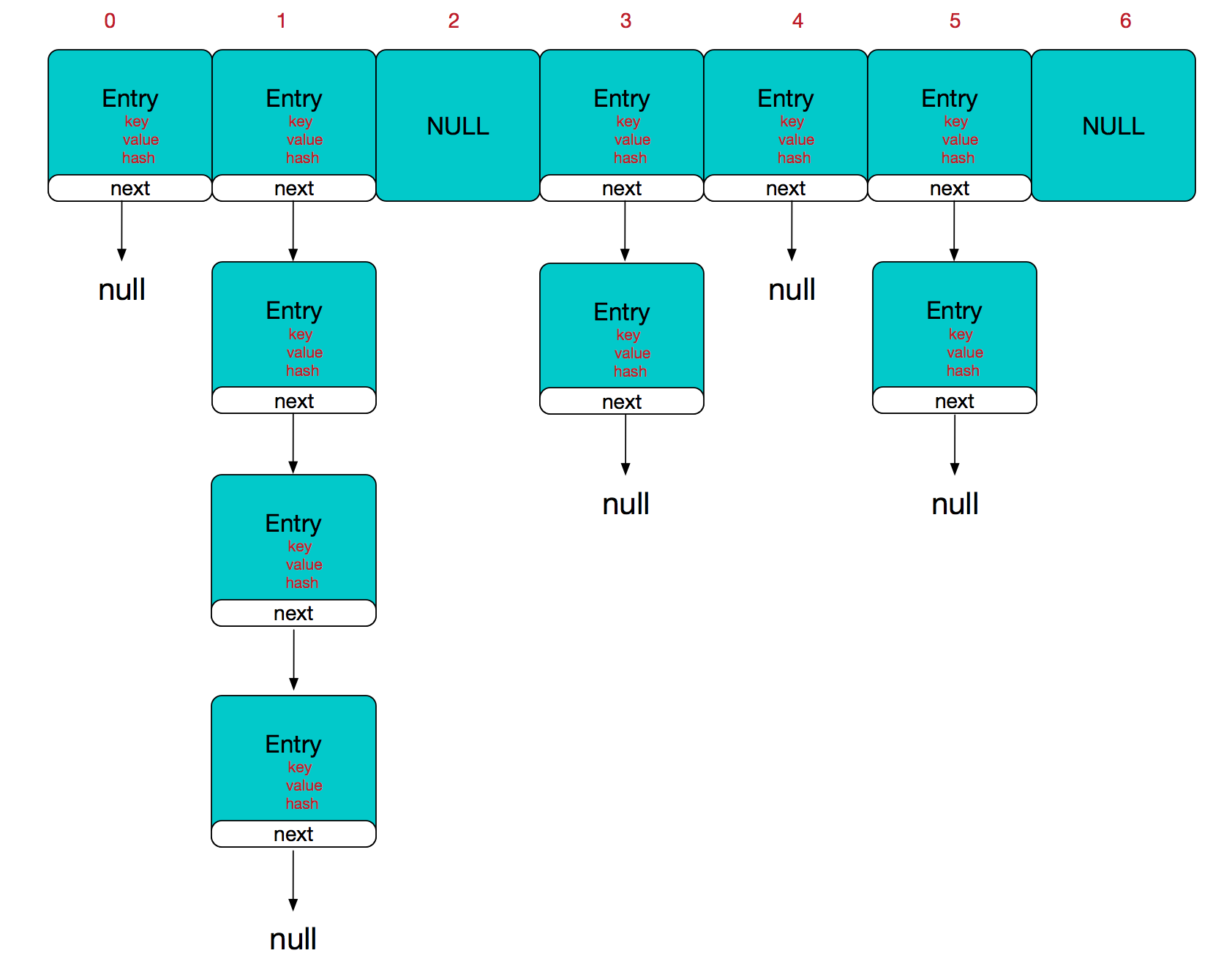

Simply put, HashMap is made up of an array + a list of chains, which is the main body of HashMap, and a list of chains exists primarily to resolve hash conflicts, if the location of the array you locate does not contain a list of chains (the next entry of the current entry points to null).Find, add, and so on are quick operations, only need one addressing; if the array located contains a list of chains, for add operations, the time complexity is O(n), first traverse the list of chains, existing is overwritten, otherwise new; for find operations, still need to traverse the list of chains, and then compare one by one through the key equals method of the keyobject.Therefore, for performance reasons, the fewer chains in HashMap, the better the performance.

Several other important fields

/**Number of key-value pairs actually stored*/
transient int size;

/**Threshold, which is the initial capacity when table == {} (default is 16); when the table is filled, that is, after allocating memory space for the table,
threshold Typically, it is capacity*loadFactory.HashMap needs to refer to threshold when expanding, which will be discussed in more detail later*/
int threshold;

/**Load factor, which represents how full the table is, defaults to 0.75
The reason for the load factor is also to alleviate hash conflicts. If the initial bucket is 16 and waits until 16 elements are full to expand, there may be more than one element in some buckets.
So the load factor defaults to 0.75, which means that a HashMap of size 16 expands to 32 by the 13th element.
*/
final float loadFactor;

/**HashMap Number of times HashMap has been changed, because HashMap is non-thread safe, when iterating over HashMap,
If the participation of other threads during the period causes the structure of HashMap to change (such as put, remove, and so on),
ConcurrentModificationException needs to be thrown*/
transient int modCount;

HashMap has four constructors, and the others use default values if the user does not pass in two parameters, initialCapacity and loadFactor

The default is 16 for initialCapacity and 0.75 for loadFactory

Let's look at one of them

public HashMap(int initialCapacity, float loadFactor) {
　　　　　//The incoming initial capacity is checked here and cannot exceed MAXIMUM_CAPACITY = 1< 30 (230)
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);

        this.loadFactor = loadFactor;
        threshold = initialCapacity;
　　　　　
        init();//The init method is not actually implemented in HashMap, but is implemented in its subclasses such as linkedHashMap
    }

From the above code, we can see that in the general constructor, there is no memory space allocated for the array table (with one exception for the constructor that takes part in the specified Map), but the table array is actually built when the put operation is performed.

OK, let's look at the implementation of put

public V put(K key, V value) {
        //If the table array is an empty array {}, fill the array (allocate the actual memory space for the table) with threshold.
        //threshold is initialCapacity at this time defaults to 1 < 4 (24=16)
        if (table == EMPTY_TABLE) {
            inflateTable(threshold);
        }
       //If the key is null, the storage location is on the conflict chain of table[0] or table[0]
        if (key == null)
            return putForNullKey(value);
        int hash = hash(key);//Further hashcode calculation of key to ensure even hash
        int i = indexFor(hash, table.length);//Get the actual location in the table
        for (Entry<K,V> e = table[i]; e != null; e = e.next) {
        //If the corresponding data already exists, perform the overwrite operation.Replace the old value with the new value and return the old value
            Object k;
            if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                V oldValue = e.value;
                e.value = value;
                e.recordAccess(this);
                return oldValue;
            }
        }
        modCount++;//Fast response fails when HashMap internal structure changes while guaranteeing concurrent access
        addEntry(hash, key, value, i);//Add a new entry
        return null;
    }

The inflateTable method is used to allocate storage space in memory for the main array table. roundUpToPowerOf2(toSize) ensures that capacity is the closest toSize power greater than or equal to toSize, for example, toSize=13, capacity=16; to_size=16; to_size=17, capacity=32.

private void inflateTable(int toSize) {
        int capacity = roundUpToPowerOf2(toSize);//capacity must be a power of 2
        /**This assigns a value to threshold s, taking the minimum values of capacity*loadFactor and MAXIMUM_CAPACITY+1.
        capaticy Must not exceed MAXIMUM_CAPACITY unless loadFactor is greater than 1 */
        threshold = (int) Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);
        table = new Entry[capacity];
        initHashSeedAsNeeded(capacity);
    }

This processing in roundUpToPowerOf2 makes the length of the array a power of 2, and Integer.highestOneBit is used to get the number represented by the leftmost bit (other bit is 0).

 private static int roundUpToPowerOf2(int number) {
        // assert number >= 0 : "number must be non-negative";
        return number >= MAXIMUM_CAPACITY
                ? MAXIMUM_CAPACITY
                : (number > 1) ? Integer.highestOneBit((number - 1) << 1) : 1;
    }

hash function

/**This is a magical function that uses a lot of XOR, shift, and so on.
Further calculation of the hashcode of the key and adjustment of the binary bits ensure that the evenly obtained storage locations are as evenly distributed as possible.*/
final int hash(Object k) {
        int h = hashSeed;
        if (0 != h && k instanceof String) {
            return sun.misc.Hashing.stringHash32((String) k);
        }

        h ^= k.hashCode();

        h ^= (h >>> 20) ^ (h >>> 12);
        return h ^ (h >>> 7) ^ (h >>> 4);
    }

The value calculated by the hash function above is further processed by indexFor to obtain the actual storage location

    /**
     * Return Array Subscript
     */
    static int indexFor(int h, int length) {
        return h & (length-1);
    }

H &(length-1) guarantees that the index obtained is within the range of the array. For example, the default capacity is 16, length-1=15, h=18, which is converted to binary computation to index=2.Bit operations are more efficient for computers (HashMap has a lot of bit operations)

So the process for determining the final storage location is as follows:

Let's also look at the implementation of addEntry:

void addEntry(int hash, K key, V value, int bucketIndex) {
        if ((size >= threshold) && (null != table[bucketIndex])) {
            resize(2 * table.length);//Expansion when size exceeds critical threshold and a hash conflict is imminent
            hash = (null != key) ? hash(key) : 0;
            bucketIndex = indexFor(hash, table.length);
        }

        createEntry(hash, key, value, bucketIndex);
    }

The code above tells you that when a hash conflict occurs and the size is greater than the threshold, you need to expand the array. When you expand, you need to create a new array that is twice as long as the previous one, and then transfer all the elements in the current Entry array. The new expanded array is twice as long as the previous one, so the expansion is a relatively resource-intensive operation.

3. Why must the length of the HashMap array be a power of two?

Let's continue with the resize method mentioned above

void resize(int newCapacity) {
        Entry[] oldTable = table;
        int oldCapacity = oldTable.length;
        if (oldCapacity == MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return;
        }

        Entry[] newTable = new Entry[newCapacity];
        transfer(newTable, initHashSeedAsNeeded(newCapacity));
        table = newTable;
        threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
    }

If the array is expanded, the length of the array changes, and the storage location index = H & (length-1), the index may also change. You need to recalculate the index. Let's first look at transfer

void transfer(Entry[] newTable, boolean rehash) {
        int newCapacity = newTable.length;
　　　　　//The code in the for loop iterates through the list one by one, recalculates the index position, and copies the old array data into the new array (the array does not store the actual data, so it is just a copy reference)
        for (Entry<K,V> e : table) {
            while(null != e) {
                Entry<K,V> next = e.next;
                if (rehash) {
                    e.hash = null == e.key ? 0 : hash(e.key);
                }
                int i = indexFor(e.hash, newCapacity);
                //Pointing the current entry's next chain to the new index location, newTable[i] may be empty, it may also be an entry chain, if it is an entry chain, it is inserted directly in the chain header.
                e.next = newTable[i];
                newTable[i] = e;
                e = next;
            }
        }
    }

This method traverses the data in the old array one by one and throws it into the new expanded array. Our array index position is calculated by hash-scrambling the hashcode of the key value, and then by bitwise operation with length-1 to get the final array index position.

HashMap's array length must be a power of 2, such as 16 represented by 10,000 binary, then length-1 is 15, binary is 01111, similarly expanded array length is 32, binary is 100000, length-1 is 31, binary is 011111.As we can also see from the following figure, this guarantees that the low bit is all 1, and there is only one difference after expansion, that is, there is more than one left-most bit, so it passes through theWhen H & (length-1), as long as the leftmost difference bit corresponding to h is 0, the new array index and the old array index are guaranteed to be identical (greatly reducing the data position re-swapping of old arrays that had been well hashed before), which is understandable by the individual.

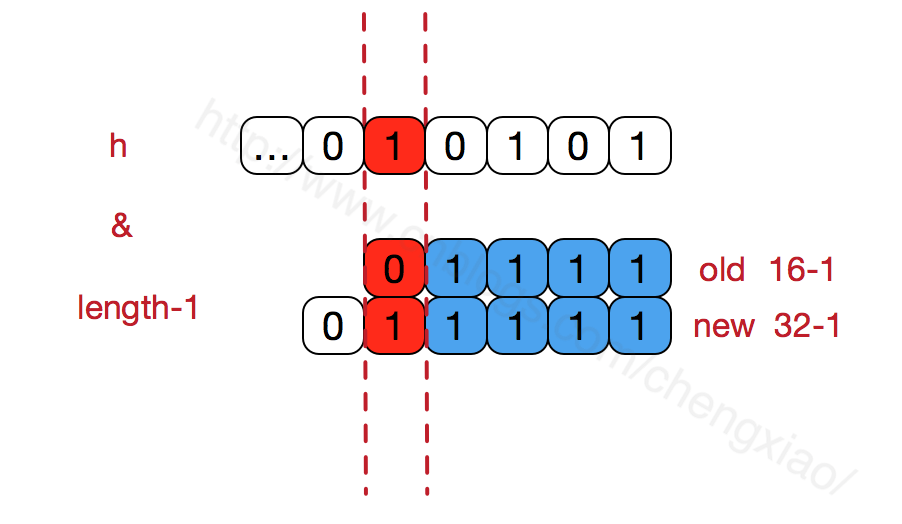
Also, keeping the length of the array to a power of 2 and the low bit of length-1 to 1 makes the index index of the array more even

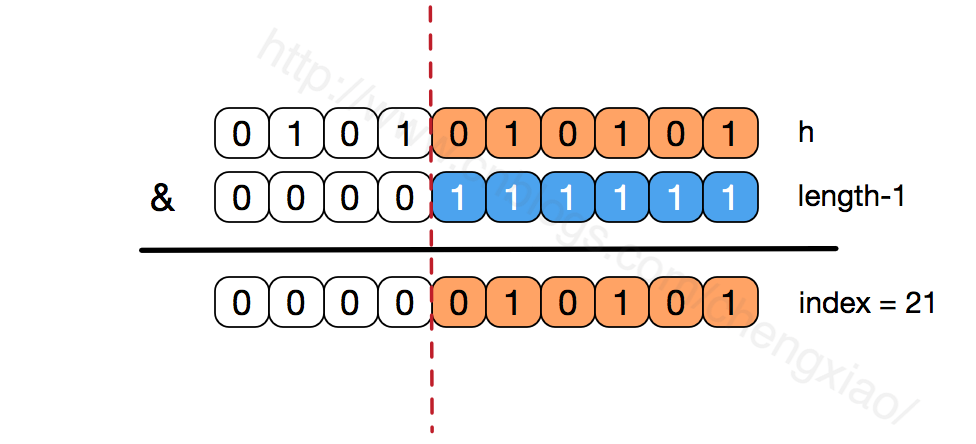
As we can see from the above &operation, the higher bits will not affect the results (hash functions use various bit operations may also be used to make the lower bits more hashed). We only focus on the lower bits. If the lower bits are all 1, then any change in the lower part of h will affect the results, that is, to get the storage location index=21, h'sLow is the only combination.This is why the length of the array is designed to be a power of two.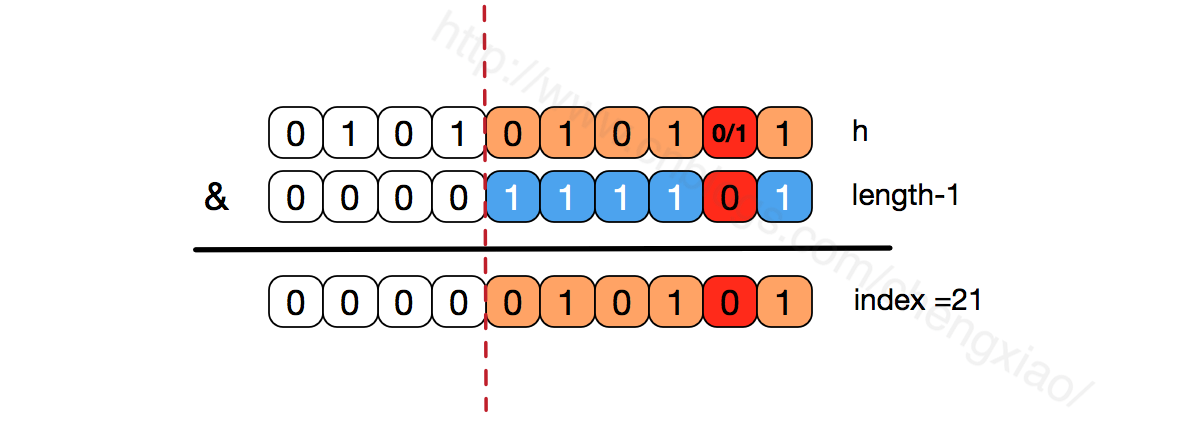

If it is not the power of 2, that is, if the low bit is not all 1, then the lower part of h will no longer be unique in order to make index=21, and the probability of hash conflict will become greater. Meanwhile, the bit bit of index will not equal 1 in any case, and the corresponding array positions will be wasted.

get method:

 public V get(Object key) {
　　　　 //If the key is null, go directly to table[0] to retrieve it.
        if (key == null)
            return getForNullKey();
        Entry<K,V> entry = getEntry(key);
        return null == entry ? null : entry.getValue();
 }

The get method returns the corresponding value through the key value, and if the key is null, it retrieves it directly at table[0].Let's look at the getEntry method again

final Entry<K,V> getEntry(Object key) {
            
        if (size == 0) {
            return null;
        }
        //Calculate hash value from hashcode value of key
        int hash = (key == null) ? 0 : hash(key);
        //IndexFor (hash&length-1) gets the final array index, then traverses the chain table to find the corresponding record by comparing the equals method
        for (Entry<K,V> e = table[indexFor(hash, table.length)];
             e != null;
             e = e.next) {
            Object k;
            if (e.hash == hash && 
                ((k = e.key) == key || (key != null && key.equals(k))))
                return e;
        }
        return null;
    }    

You can see that the get method is relatively simple to implement, key(hashcode) ->hash->indexFor->the final index location, find the corresponding location table[i], check whether there is a chain table, traverse the chain table, and compare the keys equals method to find the corresponding records.It is important to note that the e.hash == hash judgment is not necessary when the above is located after the array position and then traversed the list of chains, it can only be determined by equals.In fact, imagine that if the incoming key Object overrides the equals method but does not override hashCode, and this Object happens to be positioned at this array location, if only equals is used to determine that it may be equal, but its hashCode is inconsistent with the current Object, in which case, according to the Convention of the Object's hashCode, the current Object cannot be returned, but null should be returned, as in the following exampleThe child will explain it further.

4. Rewriting equals method requires rewriting hashCode method at the same time

Finally, let's talk about one of the old questions. It's mentioned in various materials that "override hashcode when you rewrite equals." Let's take a small example to see what happens if you rewrite equals without rewriting hashcode.

public class MyTest {
    private static class Person{
        int idCard;
        String name;

        public Person(int idCard, String name) {
            this.idCard = idCard;
            this.name = name;
        }
        @Override
        public boolean equals(Object o) {
            if (this == o) {
                return true;
            }
            if (o == null || getClass() != o.getClass()){
                return false;
            }
            Person person = (Person) o;
            //Whether two objects are equal or not, determined by idCard
            return this.idCard == person.idCard;
        }

    }
    public static void main(String []args){
        HashMap<Person,String> map = new HashMap<Person, String>();
        Person person = new Person(1234,"Look crazy");
        //put into hashmap
        map.put(person,"Eight parts of Dragon");
        //Gett out, logically it should be able to output "Eight parts of Dragon"
        System.out.println("Result:"+map.get(new Person(1234,"Xiao Feng")));
    }
}

//Actual output: null

If we already have some understanding of the principles of HashMap, the results will not be difficult to understand.Although the keys used in the get and put operations are logically equal (compared by equals), since hashCode methods are not overridden, the key(hashcode1) - >hash ->indexFor -> final index position is used in the put operation, and the value is taken out by the keyKey (hashcode1) - > hash -> indexFor -> final index location, since hashcode1 is not equal to hashcode2, returns the logically incorrect value null without locating at an array location (it may also happen to locate at an array location, but it also determines whether the hash values of its entries are equal, as mentioned in the get method above.)

Therefore, when overriding the equals method, care must be taken to override the hashCode method, while ensuring that equals determines two equal objects and that the hashCode method is called to return the same integer value.If equals judges two objects that are not equal, their hashCodes can be the same (but hash conflicts should be avoided as much as possible).

5. Performance optimization of HashMap in JDK1.8

What if too much data in the chain on an array slot (i.e. too long zipper) causes performance degradation?
JDK1.8 is based on JDK1.7 to optimize for the addition of red and black trees.That is, when the chain table exceeds 8, the chain table is converted to a red-black tree, which improves the performance of HashMap by taking advantage of the fast growth, deletion, and search of the red-black tree.
We will discuss this in a future article.
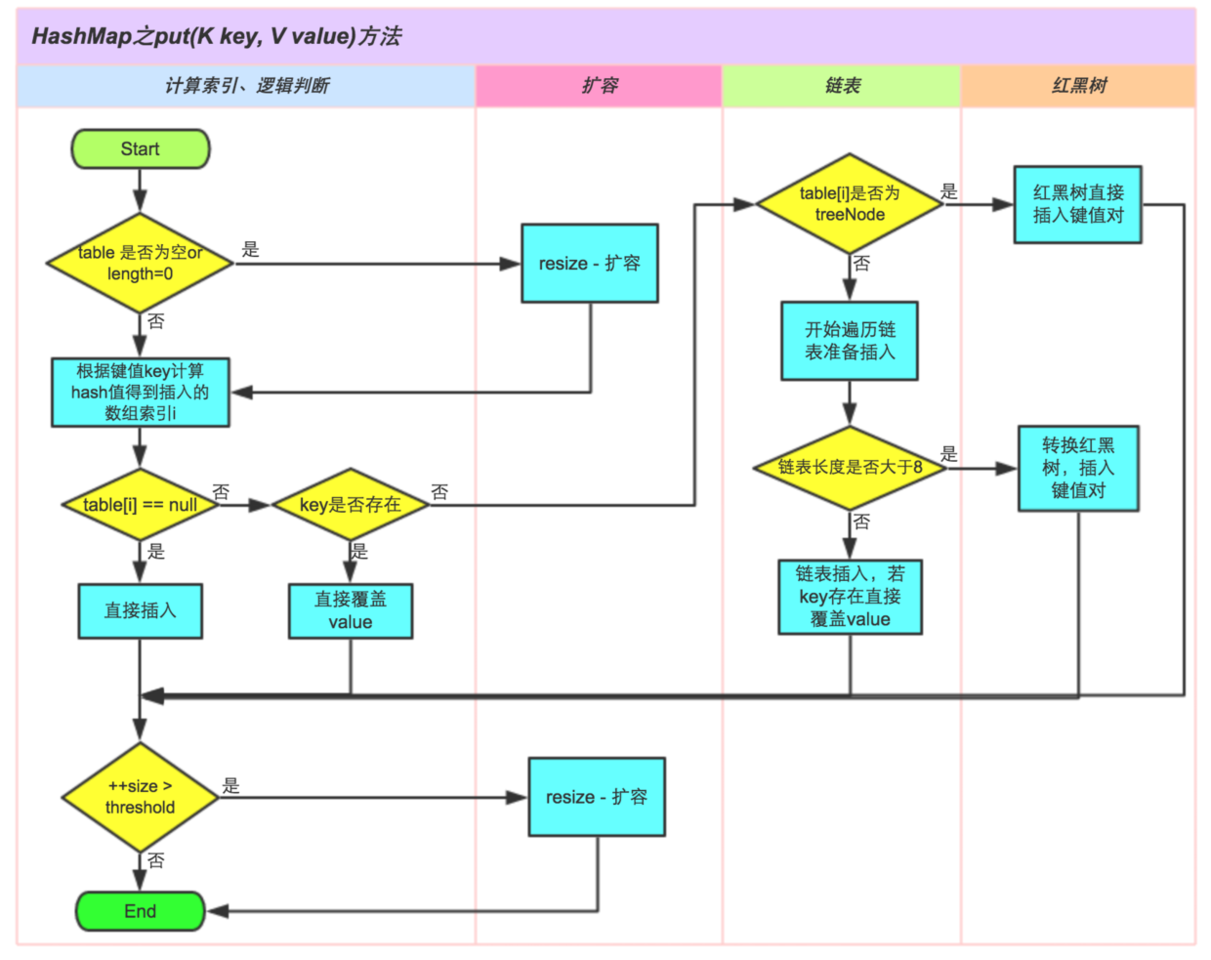
Attachment: HashMap put method logic diagram (JDK1.8)