Title: give you a set. Each element of the set is an interval. You need to remove the repeated interval and return to the new set. eg: give you a set [1,3], [2,6], [8,10], [15,18], the set after eliminating repetition is: [1,6], [8,10], [15,18]

Thought: when I started to do this problem, I was wrong in thinking. I divided it into left section and right section and considered them separately. After a long time, I didn't work it out. Later, after a flash of inspiration and overall consideration, I found that there are only six situations that need to be dealt with: left separation, right separation, left intersection, right intersection, inclusion and equality, inclusion and equality (not to be dealt with), as shown in the following figure:

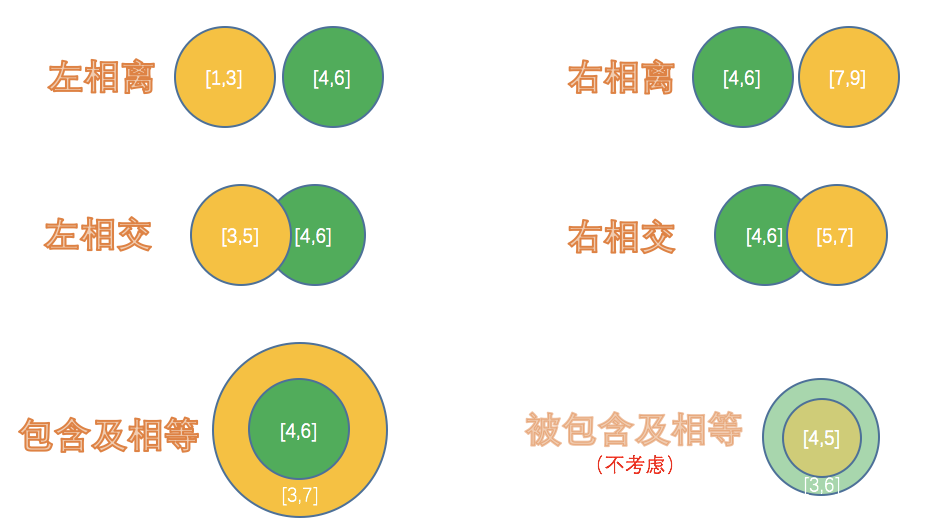
It's easy to solve problems according to these six situations, and it's easy to understand the code:

/**
 * Definition for an interval.
 * struct Interval {
 *     int start;
 *     int end;
 * };
 */
/**
 * Return an array of size *returnSize.
 * Note: The returned array must be malloced, assume caller calls free().
 */
struct Interval* merge(struct Interval* intervals, int intervalsSize, int* returnSize) {
    if (intervalsSize == 0) return intervals;
    struct Interval* result = malloc(sizeof(intervals) * intervalsSize);
    result[0].start = intervals[0].start;
    result[0].end = intervals[0].end;
    //Record subscript
    int index = 1;
    for (int i = 1; i < intervalsSize; i++) {
        //Right separation (added)
        if (intervals[i].start > result[index-1].end) {
            result[index].start = intervals[i].start;
            result[index].end = intervals[i].end;
            index++;
        //Left separated (inserted in front)
        }else if (intervals[i].end < result[index-1].start) {
            if (index == 1) {
                result[1].start = result[0].start;
                result[1].end = result[0].end;
                result[0].start = intervals[i].start;
                result[0].end = intervals[i].end;
                index++;
            }else {
                intervals[i-1].start = intervals[i].start;
                intervals[i-1].end = intervals[i].end;
                intervals[i].start = result[index-1].start;
                intervals[i].end = result[index-1].end;
                index--;
                i -= 2;
            }
        //Left intersection
        }else if (intervals[i].start < result[index-1].start && intervals[i].end <= result[index-1].end) {
            if (index == 1) result[0].start = intervals[i].start;
            else {
                intervals[i].end = result[index-1].end;
                I--;
                index--;
            }
        //Right intersection
        }else if (intervals[i].start >= result[index-1].start && intervals[i].end > result[index-1].end) {
            result[index-1].end = intervals[i].end;
        //Inclusive and equivalent
        }else if (intervals[i].start < result[index-1].start && intervals[i].end > result[index-1].end) {
            if (index == 1) {
                result[0].start = intervals[i].start;
                result[0].end = intervals[i].end;
            }else {
                index--;
                I--;
            }
        }
    }
    *returnSize = index;
    return result;
}

By solving this problem, I also learned a structure pointer by the way. In the previous algorithm problems, I often used the chain table as the container. When the low burst, it's not very good to use the structure pointer directly (except for the two-way chain table)...

Copyright notice: This article is the original production of Crazy Steven, welcome to reprint, please indicate the source when reprint!