Luogu P3805 manacher algorithm

Horse drawn cart algorithm is an algorithm for finding the longest palindrome string. Its core is to reduce redundant repeated calculation, and use the currently known data to deduce the subsequent data as much as possible, so as to achieve linear complexity.

I think the core of this algorithm is to make full use of the symmetry of palindrome string.

The first is a small skill to deal with palindrome strings. For odd and even palindrome strings, we only need to add a '#' character between two adjacent characters, so both odd strings and even strings will become odd strings (self simulation).

For the palindrome string \ ([1,mx] \) you have found, define \ (mid \) as the palindrome center of the string, and the p[i] array represents the longest palindrome radius with \ (I \) as the palindrome center.

First, a conclusion is given that the length of the longest palindrome string of a string centered on \ (I \) will be equal to p[i]-1 because a '#' will be subtracted.

So how to do \ (manacher \)?

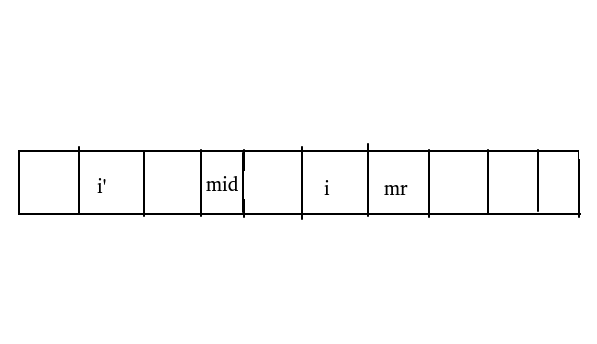
For a \ (I (mid < I < MX) \), according to the symmetry, the symmetry point \ (I '\) of \ (I \) is \ (mid*2-i \), so the longest palindrome radius with \ (I \) as the palindrome center must not be less than the longest palindrome radius with \ (I' \) as the palindrome center, so we can let p[i]=min(p[mid*2-i],mx-i) (note that the length of palindrome radius cannot exceed \ (mx-i \)), Then, determine one by one the palindrome strings in which \ (I \) exceeds the range of \ (MX \), and update \ (MX \) and \ (mid \) repeatedly. Finally, it can be found.

What if \ (I (mx < I) \)? Just consider the violence request directly, and then update \ (mx \) and \ (mid \).

#include<bits/stdc++.h>
using namespace std;
const int N=3e7+5;
int cnt,p[N],ans;
char s[N];
void read(char *str){
  char ch=getchar();
  str[0]='@';
  while(ch>='a'&&ch<='z') str[++cnt]='#',str[++cnt]=ch,ch=getchar();
  str[++cnt]='#';
}
int main(){
  read(s);
  int mid=1,mx=1;
  for(int i=1;i<cnt;i++){
    if(i<mx){
      p[i]=min(p[(mid<<1)-i],mx-i);
    }
    else p[i]=1;
    while(s[i-p[i]]==s[i+p[i]]) p[i]++;
    if(mx<i+p[i]){
      mx=i+p[i];
      mid=i;
    }
    ans=max(ans,p[i]-1);
  }
  printf("%d",ans);
  return 0;
}

Luogu P1368 minimum representation

The minimum representation is to find the smallest one of her cyclic isomorphic strings for a string.

For example, the string "gfedcba", her cyclic isomorphic string is:

"agfedcb"，"bagfedc"，"cbagfed"，"dcbagfe"，"edcbagf"，"fedcbag"

So obviously, for her, her minimum representation is "agfedcb".

Consider how to find the minimum representation of a string

Note: save the string here from \ (0 \).

We define two pointers \ (i \) and \ (j \), which respectively point to two different positions in the string \ (s \) (it is meaningless when the pointing positions are the same). We define that currently \ (k \) characters have been matched from \ (i \) and \ (j \) (starting from \ (i \), \ (j \), including that the last \ (k \) characters of \ (i \) and \ (j \) are equal).

Then for s[(i+k)%n] and s[(j+k)%n]:

• If equal, then the matching number k + +;

• If s [(i + k)% n] > s [(j + k)% n], the characters between \ (i \ SIM, i + K \) will not be the beginning of the minimum representation, so \ (i \) directly jumps to \ (i+k+1 \);

• If s [(I + k)% n] < s [(j + k)% n], similarly, it can be obtained that \ (J \) jumps to \ (j+k+1 \).

Finally, the point with the smallest position of \ (i \) and \ (j \) is the starting point of the minimum representation, which is recorded as \ (ans \). Finally, output s[(i+ans)%n].

One thing to note is that \ (i \) cannot be equal to \ (j \), because it must point to different positions, otherwise it will always match, so let i + + when equal.

#include<bits/stdc++.h>
using namespace std;
inline int read(){
  int ans=0,f=1;char ch=getchar();
  while(!isdigit(ch)){if(ch=='-') f=-f;ch=getchar();}
  while(isdigit(ch)){ans=(ans<<3)+(ans<<1)+ch-48;ch=getchar();}
  return ans*f;
}
const int N=3e5+5;
int n,ans;
int s1[N];
int minshow(){
  int i=0,j=1,k=0;
  while(i<n&&j<n&&k<n){
    if(s1[(i+k)%n]==s1[(j+k)%n]) k++;
    else{
      if(s1[(i+k)%n]>s1[(j+k)%n]) i+=k+1;
      else j+=k+1;
      if(i==j) i++;
      k=0;
    }
  }
  return min(i,j);
}
int main(){
  n=read();
  for(int i=0;i<n;i++){
    s1[i]=read();
  }
  ans=minshow();
  for(int i=0;i<n;i++){
    printf("%d ",s1[(i+ans)%n]);
  }
  return 0;
}

Luogu P3375 KMP string match

Here comes the exciting wool film algorithm

The core of KMP algorithm is also the calculation to reduce duplication and redundancy.

The naive algorithm is to match the two pointers one by one. When there is a mismatch, the pattern string is matched from the beginning. Complexity can be stuck to \ (O (nm) \)

After KMP mismatch, instead of starting from scratch, use a kmp[j] array to record where \ (J \) should start to match again after \ (j+1 \) mismatch. Moreover, it is easy to find that the pointer of the text string only increases but not decreases, and the pointer of the mode string will decrease and increase (because only changing the pointer position of the mode string after each mismatch).

Above:

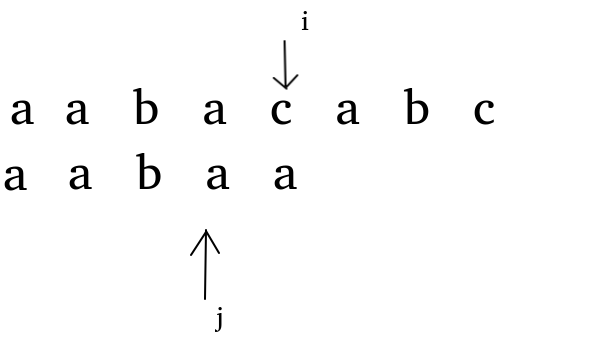
Now a [i]= B [J + 1] mismatch.

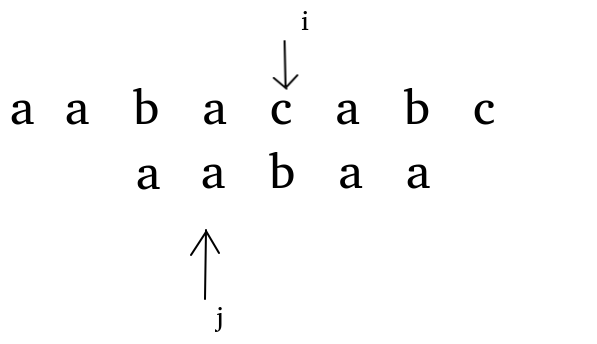
So we move \ (j \) from \ (4 \) to \ (2 \) and start matching again to avoid matching from scratch.

Let's first assume that we have found the kmp array, so the problem is very simple.

We only use double pointers to match in turn. When the mismatch occurs, we make the pattern string pointer j=kmp[j], and then re match it with the text string.

The code is as follows:

j=0;
  for(int i=1;i<=lena;i++){
    while(j&&a[i]!=b[j+1]) j=kmp[j];//If not, the pattern string jumps forward
    if(a[i]==b[j+1]) j++;//If equal, match the next bit
    if(j==lenb){//Output start position after finding the same string
      printf("%d\n",i-lenb+1);
      j=kmp[j];//Jump back
    }
  }

In order to make the pointer jump back as few as possible, we need to make the points that can be jumped back stored in the kmp[j] array as large as possible, so we can make the kmp[j] array as the longest length of the part with the same prefix and suffix from the \ (1 \sim j-1 \) bit. This allows the pointer to jump back as little as possible each time.

So how to find the kmp[j] array?

In fact, it is to use the pattern string to do KMP operation on the pattern string itself

quote Matrix67 Blog The clever proof in is

The code is as follows:

j=0;
  for(int i=2;i<=lenb;i++){
    while(j&&b[i]!=b[j+1]) j=kmp[j];
    if(b[i]==b[j+1]) j++;
    kmp[i]=j;
  }

How does complexity prove?

quote \(rqy\) Big man's proof

Each time the position pointer \ (i + + \), the mismatch pointer \ (j \) increases at most once, so \ (j \) increases at most \ (len \) times, thereby reducing at most \ (len \) times, so it is \ (\ Theta(len_N + len_M) = \Theta(N + M) \).

So far, we have finished the wool chip algorithm

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
char a[N],b[N];
int lena,lenb;
int kmp[N],j;
int main(){
  cin>>a+1;
  cin>>b+1;
  lena=strlen(a+1),lenb=strlen(b+1);
  j=0;
  for(int i=2;i<=lenb;i++){
    while(j&&b[i]!=b[j+1]) j=kmp[j];
    if(b[i]==b[j+1]) j++;
    kmp[i]=j;
  }
  j=0;
  for(int i=1;i<=lena;i++){
    while(j&&a[i]!=b[j+1]) j=kmp[j];
    if(a[i]==b[j+1]) j++;
    if(j==lenb){
      printf("%d\n",i-lenb+1);
      j=kmp[j];
    }
  }
  for(int i=1;i<=lenb;i++) printf("%d ",kmp[i]);
  return 0;
}

Luogu P3808 AC automata (simple version)

AC automata, fully known as "Aho_Corasick_Automaton", is used to solve the problem of multiple pattern strings matching a text string. Associating with the previously learned algorithms, it is found that there is a KMP algorithm (watching wool chips) that can solve the problem of matching a pattern string with a text string. Then, using the x-set x idea, one of the basic ideas of OI, can we consider combining the two algorithms to achieve a magical effect?

We found that for multiple pattern strings, we can build a \ (trie \) tree to find their common prefix, and then we can see the wool piece KMP on the \ (trie \) tree!

As we all know, the most important thing in KMP is the mismatch array fail. How can we find the fail array on the \ (trie \) tree?

It's very simple. Just run one side \ (bfs \). The logic is very clear. Just look at the code. I won't repeat it. Pay attention to optimization!

void build(){
  for(int i=0;i<26;i++) if(trie[0][i]) fail[trie[0][i]]=0,q.push(trie[0][i]);
  while(!q.empty()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(trie[u][i]) fail[trie[u][i]]=trie[fail[u]][i],q.push(trie[u][i]);
      else trie[u][i]=trie[fail[u]][i];//Optimization. If you don't have this edge, you should jump back sooner or later. It's better to jump now
    }
  }
}

With the \ (fail \) array, how do you match it?

It is also very simple. We only need to traverse, enumerate the edges to which the characters of the current text string are connected, then run all the \ (fail \) of these points aside, and then add the end mark \ (end \) directly to the answer. Be careful not to double calculate, and discard the used marks!

int query(char *str){
  int len=strlen(str),p=0,res=0;
  for(int i=0;i<len;i++){
    p=trie[p][str[i]-'a'];
    for(int t=p;t&&end[t]!=-1;t=fail[t]) res+=end[t],end[t]=-1;
  }
  return res;
}

Finally, pay attention to constant optimization. Don't use the code on the blue book for this problem. It's always stuck. It's useless if oxygen inhalation is poisoned.

code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n;
int trie[N][26],end[N],fail[N],tot;
queue<int> q;
void ins(char *str){
  int len=strlen(str),p=0;
  for(int i=0;i<len;i++){
    int ch=str[i]-'a';
    if(!trie[p][ch]) trie[p][ch]=++tot;
    p=trie[p][ch];
  }
  end[p]++;
}
void build(){
  for(int i=0;i<26;i++) if(trie[0][i]) fail[trie[0][i]]=0,q.push(trie[0][i]);
  while(!q.empty()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(trie[u][i]) fail[trie[u][i]]=trie[fail[u]][i],q.push(trie[u][i]);
      else trie[u][i]=trie[fail[u]][i];
    }
  }
}
int query(char *str){
  int len=strlen(str),p=0,res=0;
  for(int i=0;i<len;i++){
    p=trie[p][str[i]-'a'];
    for(int t=p;t&&end[t]!=-1;t=fail[t]) res+=end[t],end[t]=-1;
  }
  return res;
}
char tmp[N];
int main(){
  cin>>n;
  for(int i=1;i<=n;i++) cin>>tmp,ins(tmp);
  build();
  cin>>tmp;
  printf("%d",query(tmp));
  return 0;
}

Luogu P5410 extended KMP (Z function)

Look at the wool film.

In fact, I think it is a bit like the combination of horse drawn cart idea and KMP, but these three algorithms are linear by reducing redundant and repeated calculations.

Compared with KMP algorithm, exKMP algorithm calculates the LCP (longest common prefix) of the suffix of pattern string and text string

We make the extend array the suffix of the text string \ (S \) and the LCP of the pattern string \ (T \), and the z array the suffix of the pattern string \ (T \) and the LCP of the pattern string \ (T \).

How to ask? Draw first.

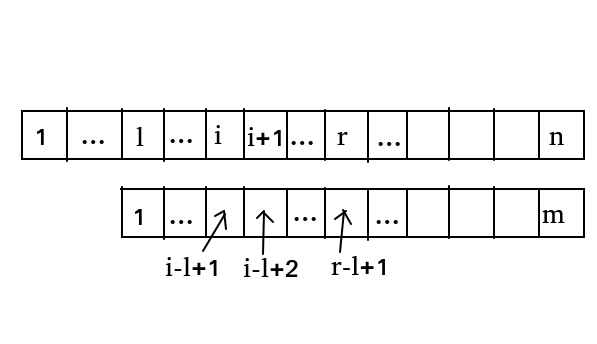
We assume that the extend array and z array of \ (1 \sim i \) have been found. In the matching process, the furthest matching distance is recorded as \ (R \), that is \ (r=max(i+extend[i]-1) \), and the \ (I \) that can get the maximum value of \ (R \) is recorded as \ (l \).

• In the first case, when \ (i+L \) is to the left of \ (r \):

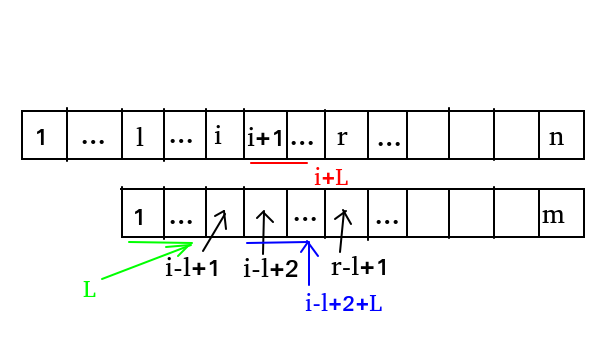
z[i-l+1] represents the longest common prefix between \ (T[i-l+2\sim m] \) and \ (T[1 \sim m] \), which is set to \ (L \).

Therefore \ (T[1\sim L]=T[i-l+2\sim i-l+2+L] \), the length characters of blue and green parts in the figure are equal (hereinafter referred to as "equal").

According to the definitions of \ (L \) and \ (r \), it can be seen that \ (S[l\sim r]=T[1\sim r-l+1] \), so \ (S[i+1\sim i+L]=T[i-l+2\sim i-l+2+L] \), the red part in the figure is equal to the blue part.

The three parts of red, green and blue in the above figure are equal

Because the longest common prefix of \ (S[i\sim n] \) and \ (T[1\sim m] \) is extend[i], extend[i]=L.

• In the second case, when \ (i+L \) is on the right of \ (r \):

We make extend[i]=r-i+1 run out of the remaining answers by violence.

So where do you start running violence?

Start running from the current \ (i \) and compare it with the pattern string one by one.

Finally, don't forget to update \ (l \) and \ (r \).

For the \ (z \) array, this algorithm is repeated.

Because each point can be run once at most, the complexity of doing it once is linear.

z and extend are done respectively, so the total time complexity is \ (\ Theta(n+m) \).

code:

#include<bits/stdc++.h>
using namespace std;
const int N=2e7+5;
char s[N],t[N];
int lens,lent;
int z[N],extend[N];
void doZ(){
  z[1]=lent;
  for(int i=2,l=0,r=0;i<=lent;i++){
    if(i<=r) z[i]=min(z[i-l+1],r-i+1);
    while(i+z[i]<=lent&&t[i+z[i]]==t[z[i]+1]) ++z[i];
    if(i+z[i]-1>r) l=i,r=i+z[i]-1;
  }
}
void exkmp(){
  doZ();
  for(int i=1,l=0,r=0;i<=lens;i++){
    if(i<=r) extend[i]=min(z[i-l+1],r-i+1);
    while(i+extend[i]<=lens&&s[i+extend[i]]==t[extend[i]+1]) ++extend[i];
    if(i+extend[i]-1>r) l=i,r=i+extend[i]-1;
  }
}
int main(){
  scanf("%s%s",s+1,t+1);
  lens=strlen(s+1);lent=strlen(t+1);
  exkmp();
  long long ans1=0,ans2=0;
  for(int i=1;i<=lent;i++) ans1^=1ll*i*(z[i]+1);
  for(int i=1;i<=lens;i++) ans2^=1ll*i*(extend[i]+1);
  printf("%lld\n%lld",ans1,ans2);
  return 0;
}

Another point is why running violence is written outside the cycle regardless of the situation, because for the above situation 1, there can be no \ (T[L+1]=S[i+L+1] \). Because if there is \ (T[L+1]=S[i+L+1] \), their longest public prefix is \ (L+1 \), and \ (L \) is not the longest public prefix, so it does not meet the definition of \ (L \). So I only run violence in case 2, which is also the ingenious simplicity of the algorithm!