Powered by:NEFU AB_IN
Tree chain subdivision
-
introduce
Divide "tree" into "chain"
-
Pre knowledge
- Segment tree
- Treelike d f s dfs dfs order
-
Main ideas
Let me briefly record the main ideas here
Learning blog: Tree chain partition CSDN blog
Learning video: Tree chain subdivision learning
The basic questions are as follows
- Operation 1: Format: 1 x y z means adding Z to the values of all nodes on the shortest path of the tree from X to y nodes
- Operation 2: Format: 2 x y means to sum the values of all nodes on the shortest path of the tree from X to y nodes
- Operation 3: Format: 3 x z means to add Z to all node values in the subtree with X as the root node
- Operation 4: Format: 4 x means to sum the values of all nodes in the subtree with X as the root node
The path on the tree needs to be maintained, such as according to d f s dfs dfs ordered 4 − 8 4-8 Add a number to 4 − 8 in order to simplify it into l o g log The operation of log can be maintained by adding a line segment tree, which is broken into a chain
- Heavy son: the child with the largest number in the current parent node, that is, each layer has only one heavy son
-
Light son: other child nodes except heavy son
-
Heavy edge: the edge between each node and its heavy son
-
Light edge: the edge between each node and its light son
-
Heavy chain: a chain of heavy edges
-
Light chain: a chain of light edges
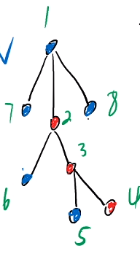
For example, in the above figure, the blue dot is the light son, and the red dot is the heavy son
According to the recursion of multiple sons, an ordered sequence can be generated. For example, in the above figure, the sequence can be generated according to the heavy chain 1 − 2 − 3 − 4 1-2-3-4 1 − 2 − 3 − 4, as for why 1 1 1 is the light son, I think in d f s 2 dfs2 dfs2 was established at the beginning t o p top top is more convenient, just put 1 1 Put it in the position of a light son
Now, if required 4 − 8 4-8 The sum of 4 − 8 chains is nothing more than two chains, one 1 − 2 − 3 − 4 1-2-3-4 1 − 2 − 3 − 4, one 1 − 8 1-8 1 − 8, the core idea is ratio 4 4 4 and 8 8 8 whose t o p top If the top is heavy, whoever jumps first. I'll explain it simply t o p top If the top is heavy, it must be below, then jumping up will be the same as the other t o p top top gather with another t o p top If it is the same as top, it is better to operate. This operation can also be used to calculate l c a lca lca
that 8 8 8 is the light son, his t o p top top is himself; 4 4 4 is a heavy son, his t o p top top is 1 1 1, then you can see 8 8 8 t o p top top deep, let 8 8 8 jump, write down 8 − 8 8-8 Sum of 8 − 8, then 8 8 8 becomes his own parent node 1 1 1. At this time 4 4 4 and 8 8 8 t o p top If the top is the same, you can use the line segment tree directly 1 − 4 1-4 Sum of 1 − 4
-
Code parsing
First, for a tree, we use the chain forward star to build the tree first
const int N = 1e6 + 10; struct Edge { int v, ne; } e[N << 2]; int h[N]; int cnt; void add(int u, int v) { e[cnt].v = v; e[cnt].ne = h[u]; h[u] = cnt++; } void init() { memset(h, -1, sizeof(h)); cnt = 0; }Second, you need to test the tree first d f s dfs dfs, the purpose is to mark the heavy son, light son, the parent node of each point and the depth of each point
int pre[N], sizx[N], son[N], deep[N]; void dfs1(int u, int fa) { pre[u] = fa; deep[u] = deep[fa] + 1; sizx[u] = 1; // The number of child nodes of the initial u node is 1 int maxson = -1; for (int i = h[u]; ~i; i = e[i].ne) { int v = e[i].v; if (v != fa) // Recursion if the child node is not the parent node { dfs1(v, u); sizx[u] += sizx[v]; // The number of child nodes of the parent node plus the number of child nodes if (maxson < sizx[v]) { maxson = sizx[v]; son[u] = v; // The son of u is v } } } }dfs1(1, 0) // The parent node of 1 is 0
After processing the data, the second time d f s dfs dfs according to heavy chain marking d f s dfs dfs order, and mark the of each node t o p top top
int cnx; // dfs2 pool int dfn[N], top[N], a[N]; void dfs2(int u, int t) // Because dfs1 has marked the heavy son, recurse according to the heavy son, and then mark the head of each son { top[u] = t; dfn[u] = ++cnx; a[cnx] = w[u]; // Record with a array, the subscript is dfs order, and the value is the initial value of the secondary node if (!son[u]) // If there is no heavy son, return return; dfs2(son[u], t); // Recursion if there is for (int i = h[u]; ~i; i = e[i].ne) { int v = e[i].v; if (v != pre[u] && v != son[u]) // If it cannot be a parent node or a son, it is a son { dfs2(v, v); //Mark the light son, the light son's head is itself } } }dfs2(1, 1) // The top of 1 is 1
The following is the part of the line segment tree, because there will be an example of interval addition + single point query of the line segment tree, so this is written
struct xds { int l, r, p, lazy; } tr[N << 2]; void pushdown(int k) { if (tr[k].lazy) { tr[k << 1].p += tr[k].lazy; tr[k << 1 | 1].p += tr[k].lazy; tr[k << 1].lazy += tr[k].lazy; tr[k << 1 | 1].lazy += tr[k].lazy; tr[k].lazy = 0; } } void build(int k, int l, int r) { tr[k].l = l; tr[k].r = r; tr[k].lazy = 0; if (l == r) { tr[k].p = a[l]; return; } int mid = l + r >> 1; build(k << 1, l, mid); build(k << 1 | 1, mid + 1, r); } void modify(int k, int ql, int qr, int w) { if (tr[k].l >= ql && tr[k].r <= qr) { tr[k].p += w; tr[k].lazy += w; return; } pushdown(k); int mid = tr[k].l + tr[k].r >> 1; if (ql <= mid) modify(k << 1, ql, qr, w); if (qr > mid) modify(k << 1 | 1, ql, qr, w); } int query(int k, int pos) //Single point query { if (tr[k].l == tr[k].r) { return tr[k].p; } pushdown(k); int mid = tr[k].l + tr[k].r >> 1; if (mid >= pos) query(k << 1, pos); else query(k << 1 | 1, pos); }build(1, 1, n)
After the line segment tree is written, the real tree chain subdivision can be carried out
void mtre(int x, int y, int z) { while (top[x] != top[y]) // Recursion until top is different { if (deep[top[x]] < deep[top[y]]) // Select the one with heavy head (i.e. large depth) and give priority to operation { swap(x, y); } modify(1, dfn[top[x]], dfn[x], z); // Use the segment tree to operate this chain (it is to operate the dfs order, not the node label) x = pre[top[x]]; // x becomes the parent of x } if (deep[x] > deep[y]) { // If the heads are the same, it means that they are on the same chain. At this time, pick the one with light head swap(x, y); } modify(1, dfn[x], dfn[y], z); } -
Examples
-
-
meaning of the title
Give you a tree, give you three operations, u u u to v v v nodes between nodes plus w w w. Subtract w w w. Query node u u Weight of u?
-
thinking
Naked tree chain segmentation problem, you can know from the operation
-
code
/* * @Author: NEFU AB_IN * @Date: 2021-09-04 18:43:00 * @FilePath: \Vscode\ACM\Project\ShuLianPaoFen\hdu3966.cpp * @LastEditTime: 2021-09-04 20:10:16 */ #include <bits/stdc++.h> using namespace std; #define LL long long #define MP make_pair #define SZ(X) ((int)(X).size()) #define IOS \ ios::sync_with_stdio(false); \ cin.tie(0); \ cout.tie(0); #define DEBUG(X) cout << #X << ": " << X << endl; typedef pair<int, int> PII; const int N = 1e6 + 10; struct Edge { int v, ne; } e[N << 2]; int h[N]; int cnt; void add(int u, int v) { e[cnt].v = v; e[cnt].ne = h[u]; h[u] = cnt++; } void init() { memset(h, -1, sizeof(h)); memset(son, 0, sizeof son); cnx = 0; cnt = 0; } int w[N]; int pre[N], sizx[N], son[N], deep[N]; int dfn[N], top[N], a[N]; int cnx; // dfs2 pool void dfs1(int u, int fa) { pre[u] = fa; deep[u] = deep[fa] + 1; sizx[u] = 1; int maxson = -1; for (int i = h[u]; ~i; i = e[i].ne) { int v = e[i].v; if (v != fa) { dfs1(v, u); sizx[u] += sizx[v]; if (maxson < sizx[v]) { maxson = sizx[v]; son[u] = v; } } } } void dfs2(int u, int t) { top[u] = t; dfn[u] = ++cnx; a[cnx] = w[u]; if (!son[u]) return; dfs2(son[u], t); for (int i = h[u]; ~i; i = e[i].ne) { int v = e[i].v; if (v != pre[u] && v != son[u]) { dfs2(v, v); } } } struct xds { int l, r, p, lazy; } tr[N << 2]; void pushdown(int k) { if (tr[k].lazy) { tr[k << 1].p += tr[k].lazy; tr[k << 1 | 1].p += tr[k].lazy; tr[k << 1].lazy += tr[k].lazy; tr[k << 1 | 1].lazy += tr[k].lazy; tr[k].lazy = 0; } } void build(int k, int l, int r) { tr[k].l = l; tr[k].r = r; tr[k].lazy = 0; if (l == r) { tr[k].p = a[l]; return; } int mid = l + r >> 1; build(k << 1, l, mid); build(k << 1 | 1, mid + 1, r); } void modify(int k, int ql, int qr, int w) { if (tr[k].l >= ql && tr[k].r <= qr) { tr[k].p += w; tr[k].lazy += w; return; } pushdown(k); int mid = tr[k].l + tr[k].r >> 1; if (ql <= mid) modify(k << 1, ql, qr, w); if (qr > mid) modify(k << 1 | 1, ql, qr, w); } int query(int k, int pos) //Single point query { if (tr[k].l == tr[k].r) { return tr[k].p; } pushdown(k); int mid = tr[k].l + tr[k].r >> 1; if (mid >= pos) query(k << 1, pos); else query(k << 1 | 1, pos); } void mtre(int x, int y, int z) { while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) { swap(x, y); } modify(1, dfn[top[x]], dfn[x], z); x = pre[top[x]]; } if (deep[x] > deep[y]) { swap(x, y); } modify(1, dfn[x], dfn[y], z); } signed main() { IOS int n, m, q; while (cin >> n >> m >> q) { init(); for (int i = 1; i <= n; ++i) { cin >> w[i]; } for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; add(u, v); add(v, u); } dfs1(1, 0); dfs2(1, 1); build(1, 1, n); while(q --){ char c; cin >> c; if(c == 'I'){ int u, v, w; cin >> u >> v >> w; mtre(u, v, w); } if(c == 'D'){ int u, v, w; cin >> u >> v >> w; mtre(u, v, -w); } if(c == 'Q'){ int u; cin >> u; cout << query(1, dfn[u]) << '\n'; } } } return 0; }
-
I rewrite the line segment tree again. I feel that this version of the line segment tree is easier to write, that is, don't forget to query and update p u s h d o w n pushdown pushdown operation
In addition, the document can be formatted with shortcut keys while writing, which can look more beautiful...
end.