1: Bubble sort (O(n^2))
The number of each position in each group is compared with the number behind it. If the number in front is greater than the number in back, exchange the number, exchange n-1 group.
Every time each group exchanges, they will put the largest row to the back, which is similar to the bubble slowly rising up in the bottom of the water.
characteristic:
stable.
Dynamic diagram demonstration:
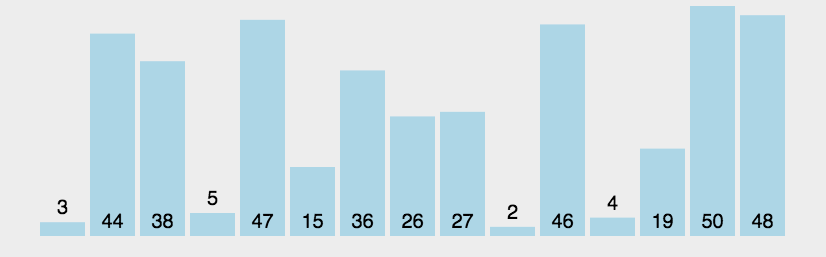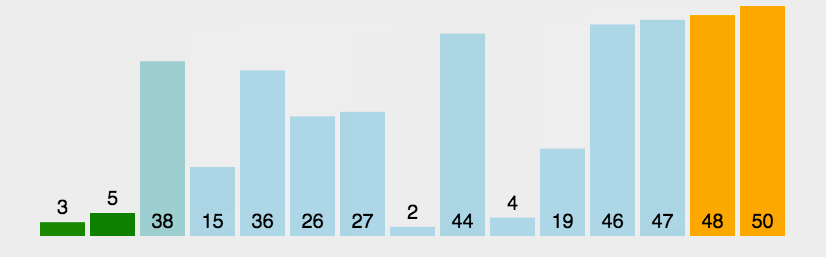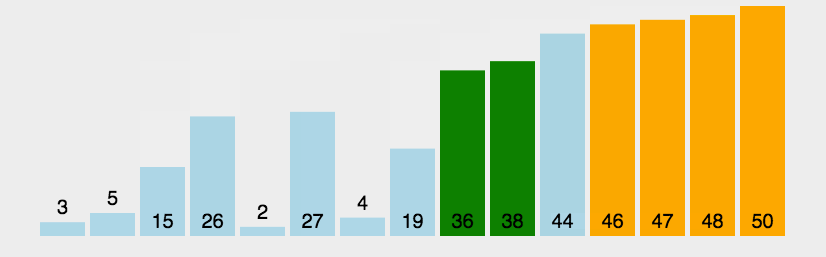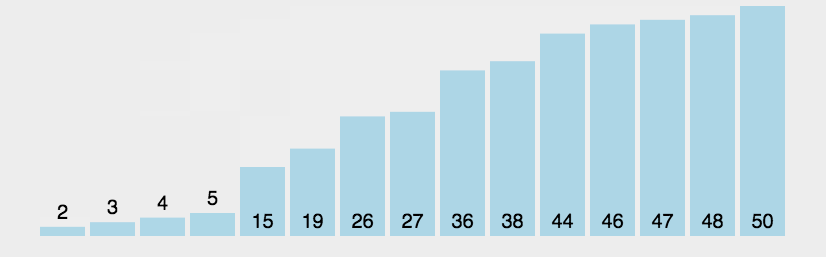
Detailed resolution code:
#include<stdio.h> int main() { int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I will set the value to the same value as the dynamic graph. int n = 15; //Bubble sorting for(int i=0;i<n-1;i++)//It's about how many group comparisons to do and why n-1 What about it? //Because the count starts at 0 and there is no need for the first number to match itself. for(int j=0;j<n-1-i;j++) //Represents the sequence number in the group, because it is to be compared with the following number, and the last number is not compared with it (it may cross the boundary) n-1 //Why-i What about it? //Because after each row, the maximum value of this group will go to the back, so there is no need to compare again. if (a[j] > a[j + 1]) { int temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } for (int i = 0;i < n;i++) printf("%d ", a[i]); return 0; }
2, Select sort (O(n^2))
Set the double loop. The first loop is used as the benchmark for comparison. The second loop looks for a smaller number behind it and exchanges it with it.
It is to select the smallest of all the smaller numbers behind it to exchange. Bubble sorting is to fix the number after it, while selection sorting is to fix the number before it.
characteristic:
The number of data moves is known (n-1).
Dynamic diagram demonstration:
Detailed resolution code:
#include<stdio.h> int main() { int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I will set the value to the same value as the dynamic graph. int n = 15; //Select sort for (int i = 0;i < n - 1;i++) // It represents the subscript of cardinality value, why n - 1 What about it? //Because the count starts at 0 and the last number doesn't compare with it. { int k = i; for (int j = i + 1;j < n;j++)//Find the lowest subscript of a number smaller than the base if (a[k] > a[j]) k = j; if (k != i) { int temp = a[k]; a[k] = a[i]; a[i] = temp; } } for (int i = 0;i < n;i++) printf("%d ", a[i]); return 0; }
3, Insert sort (O(n^2))
Starting from the second number, compare the number extracted with the previous number in turn, and move all the numbers larger than it backward one grid.
That is, put the extracted number where it should be.
characteristic:
In most cases where the elements are already ordered, insertion sorting takes less work.
Dynamic diagram demonstration:
Detailed resolution code:
#include<stdio.h> int main() { int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I will set the value to the same value as the dynamic graph. int n = 15; //Select sort for (int i = 1;i < n ;i++) // Represents the subscript to be put back to the original digit value { int front = i- 1;//Initialize the subscript of the previous number int sum = a[i];//Put back the original number of digits while (front >= 0 && a[front] > sum) //To prevent the array from going out of bounds and the front number is larger than the back number a[front + 1] = a[front--]; //Move the previous number backward, the subscript of the previous number-1,,The change of the space in the imaginary diagram //The last cycle is over, indicating that the space cannot be changed any more. Just assign it back a[++front] = sum; } for (int i = 0;i < n;i++) printf("%d ", a[i]); return 0; }
4, Merge sort O(nlog(2)n)
characteristic:
By the way, we can deal with the problem of reverse order pairs.
Dynamic diagram demonstration:
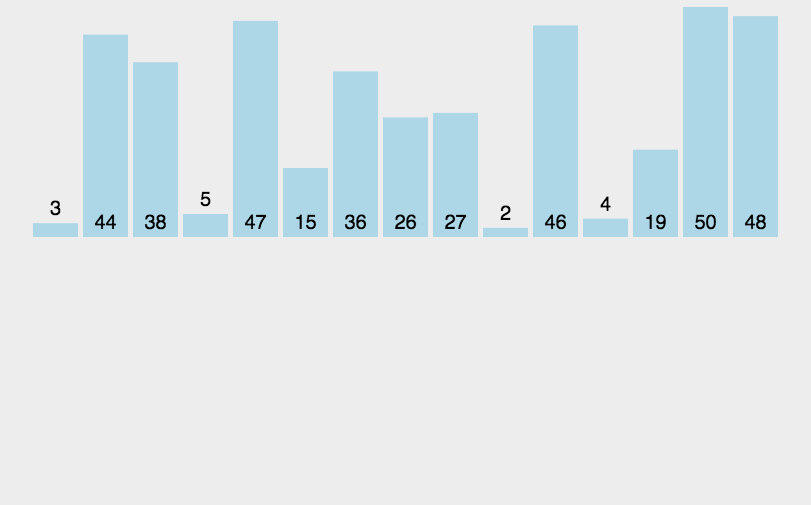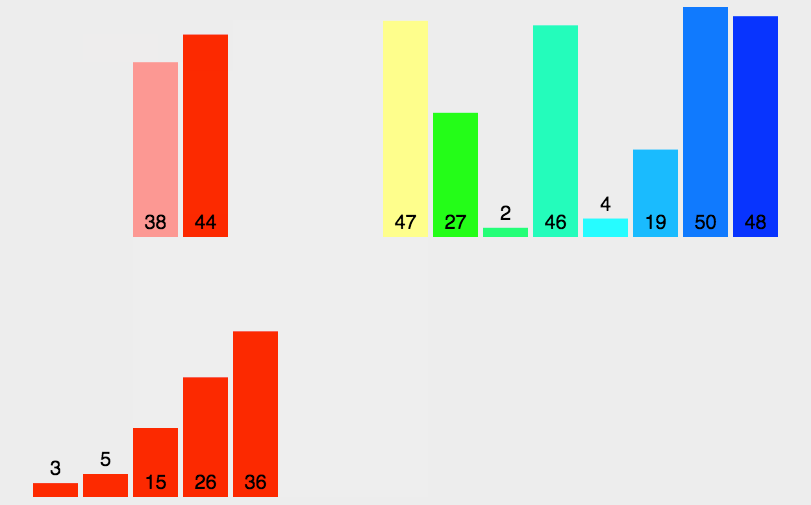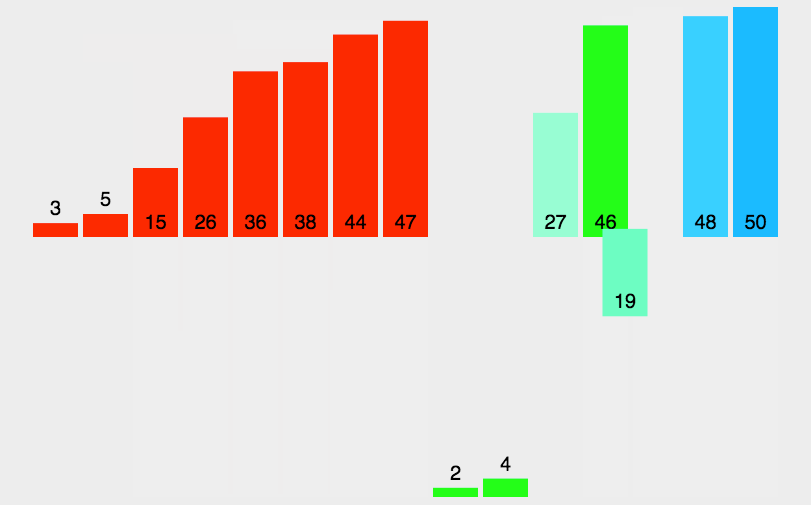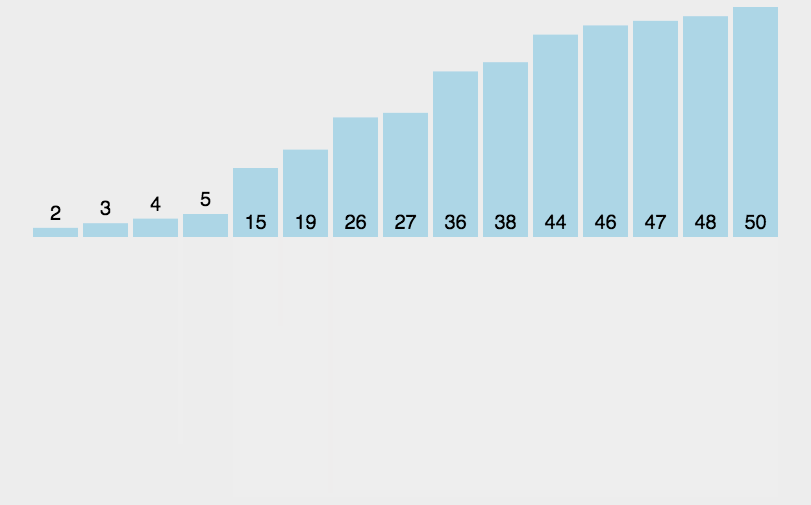
This algorithm fully embodies its idea with dynamic graph. The auxiliary array is placed below. Each part is sorted by two segments and two segments separately, and then sorted separately, and then sorted in total.
Detailed analysis code
#include<stdio.h> int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I will set the value to the same value as the dynamic graph. int t[20];//Auxiliary array, meaning of relay station. void merge_sort(int l, int r) { //If the subscripts of two arrays are adjacent, there is no need for further bisection, and there is only one bisection, which cannot be compared. if (r - l > 1) { int m = l + (r - l >> 1), i = l, j = m, k = l; //m For the middle subscript of the separated paragraph, i Is the starting point on the left, j Is the starting point on the right, k Is the starting point of the auxiliary array. //Divide the whole paragraph in two. merge_sort(l, m); merge_sort(m, r); //Then the two paragraphs are put together and sorted. while (i < m || j < r)//Prevent subscript crossing //First put into the auxiliary array must be small, so we just need to put the smaller ones on both sides into the auxiliary array. if (j >= r || (i < m && a[i] <= a[j])) t[k++] = a[i++]; //Pay attention to the problem of subscript crossing. else t[k++] = a[j++];//Here we deal with the problem of reverse order pairs. for (i = l;i < r;i++) a[i] = t[i]; } } int main() { int n = 15; merge_sort(0, n); for (int i = 0;i < n;i++) printf("%d ", a[i]); return 0; }
Reverse problem code:
#include<stdio.h> int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I will set the value to the same value as the dynamic graph. int t[20];//Auxiliary array, meaning of relay station. int ans;//Number of reverse pairs void merge_sort(int l, int r) { //If the subscripts of two arrays are adjacent, there is no need for further bisection, and there is only one bisection, which cannot be compared. if (r - l > 1) { int m = l + (r - l >> 1), i = l, j = m, k = l; //m For the middle subscript of the separated paragraph, i Is the starting point on the left, j Is the starting point on the right, k Is the starting point of the auxiliary array. //Divide the whole paragraph in two. merge_sort(l, m); merge_sort(m, r); //Then the two paragraphs are put together and sorted. while (i < m || j < r)//Prevent subscript crossing //First put into the auxiliary array must be small, so we just need to put the smaller ones on both sides into the auxiliary array. if (j >= r || (i < m && a[i] <= a[j])) t[k++] = a[i++]; //Pay attention to the problem of subscript crossing. else t[k++] = a[j++],ans+=m-i;//Here we deal with the problem of reverse order pairs. for (i = l;i < r;i++) a[i] = t[i]; } } int main() { int n = 15; merge_sort(0, n); printf("%d\n", ans); return 0; }
As long as you
else t[k++] = a[j + +]; else t[k++]=a[j++],ans+=m-i; just remember to declare the ANS variable.
The definition of reverse order pair is as follows: for the I and j elements of a sequence, if I < J and a [i] > a [J], it is a reverse order pair; otherwise, it is not.
And else just meets this condition. As long as one of them is added from the number on the right, it means that the current (left) subscript i to m-1 are greater than this number.
5, Quick sort O(nlog(2)n)
Take the middle number as the cardinal number, and compare from the left and right sides at the same time. Because the cardinal number is in the middle, the number on the left side is smaller than the cardinal number, and the number on the right side is larger than the cardinal number. Otherwise, exchange the values, and repeat the branch recursion to get the correct order.
characteristic:
It can deal with the problem of seeking the next largest one;
Disadvantages:
instable.
Detailed resolution code:
#include<stdio.h> int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I set the value to the same value as before. void quick_sort(int l, int r) { if (l < r) {//Prevention of cross-border int i = l - 1, j = r + 1, x = a[l + r >> 1]; //-1,+1 The reason is that we need to use++i,--j. //Why not i++,j++What about it? Because we're going to compare values, and we're going to let i,j Synchronization of numerical subscripts compared with us, ahead of time+1 perhaps-1 Will cause errors in subsequent exchanges. //The former is used first i+1 Again i=i+1,The latter is used first i Again i=i+1. while (i < j) { //Pause if double pointer movement does not match while (a[++i] < x); while (a[--j] > x); //Both sides don't match. Exchange values. if (i < j) {//Learn c++Can be used directly after swap Function. int t = a[i]; a[i] = a[j]; a[j] = t; } } //Divide and conquer again, and sort left and right recursively. quick_sort(l, j);quick_sort(j + 1, r); } } int main() { int n=15; quick_sort(0, n - 1); for (int i = 0;i < n;i++) printf("%d ", a[i]); return 0; }
Look for the k-th small number code:
#include<stdio.h> int a[] = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 }; //For your understanding, I set the value to the same value as before. int quick_sort(int l, int r, int k) { if (l == r) return a[l]; int i = l - 1, j = r + 1, x = a[l + r >> 1]; //-1,+1 The reason is that we need to use++i,--j. //Why not i++,j++What about it? Because we're going to compare values, and we're going to let i,j Synchronization of numerical subscripts compared with us, ahead of time+1 perhaps-1 Will cause errors in subsequent exchanges. //The former is used first i+1 Again i=i+1,The latter is used first i Again i=i+1. while (i < j) { //Pause if double pointer movement does not match while (a[++i] < x); while (a[--j] > x); //It doesn't match on both sides. Exchange the values. if (i < j) {//Learn c++Can be used directly after swap Function. int t = a[i]; a[i] = a[j]; a[j] = t; } } int s = j - l + 1;//Determine how many numbers are on the left and whether they include the k Number //Divide and rule until l==r,Output the answer. if (k <= s) return quick_sort(l, j, k); //k>s The words of K Value on the right k-s Among them, the one on the right k=k-s; return quick_sort(j + 1, r, k - s); } int main() { int n = 15, k = 5; int ans = quick_sort(0, n - 1, k); printf("%d \n", ans); return 0; }