Chapter III Search and Graph Theory
1. Depth-first search (dfs)
Search down from start to finish, find the bottom and backtrace down to finish, use stack to store data, have two concepts of backtrace and pruning, do not have the shortest
Array Array (Violent Search, Full Array)
To restore the state to its original state after backtracking
#include<iostream>
using namespace std;
const int N=10;
int path[N];
bool st[N];
int n;
void dfs(int u)
{
if(u==n)
{
for(int i=0;i<n;i++) cout<<path[i]<<" ";
cout<<endl;
return ;
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
path[u]=i;
st[i]=true;
dfs(u+1);
st[i]=false;
}
}
}
int main()
{
cin>>n;
dfs(0);
return 0;
}n-queen problem
#include<iostream>
using namespace std;
const int N=20;
int n;
char qp[N][N];
bool col[N],dg[N],udg[N];
void dfs(int u)
{
if(u==n)
{
for(int i=0;i<n;i++) puts(qp[i]);
cout<<endl;
return ;
}
for(int i=0;i<n;i++)
{
if(!col[i] && !dg[u+i] && !udg[n+i-u])
/*For rows x, the diagonals and diagonals of column y can be seen as intercept B inside function y=++x+b
You can see that the intercepts are y+x and y-x, and the second may be less than 0, so we add n to it*/
{
qp[u][i]='Q';
col[i]=dg[i+u]=udg[n+i-u]=true;
dfs(u+1);
col[i]=dg[i+u]=udg[n+i-u]=false;
qp[u][i]='.';
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
qp[i][j]='.';
}
}
dfs(0);
return 0;
}The original solution: Every grid has a queen or two
#include<iostream>
using namespace std;
const int N=20;
int n;
char qp[N][N];
bool row[N],col[N],dg[N],udg[N];
void dfs(int x,int y,int s)
{
if(y==n) y=0,x++;
if(x==n)
{
if(s==n)
{
for(int i=0;i<n;i++)
{
puts(qp[i]);
}
cout<<endl;
}
return ;
}
dfs(x,y+1,s);//Don't let Queen down
//Release Queen
if(!row[x] && !col[y] && !dg[x+y] && !udg[n+x-y])
{
qp[x][y]='Q';
row[x]=col[y]=dg[x+y]=udg[n+x-y]=true;
dfs(x,y+1,s+1);
row[x]=col[y]=dg[x+y]=udg[n+x-y]=false;
qp[x][y]='.';
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
qp[i][j]='.';
}
}
dfs(0,0,0);
return 0;
}2. Width first search (bfs)
Search from top to bottom is a bit like tree traversal, the path of the first point arrived at each time is the shortest path to the point, has the shortest property, can be used to find the shortest problem, uses queues to store, and needs exponential space.
Labyrinth problem (handwritten queue)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110;
typedef pair<int,int> PII;
int n,m;
int g[N][N];
int d[N][N];
PII q[N*N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int bfs()
{
int hh=0,tt=0;
q[0]={0,0};
memset(d, -1 ,sizeof d);
d[0][0]=0;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<4;i++)
{
int x=t.first+dx[i];
int y=t.second+dy[i];
if(x>=0 && x<n && y>=0 && y<m && g[x][y]==0 && d[x][y]==-1)
{
d[x][y]=d[t.first][t.second] +1;
q[++tt]={x,y};
}
}
}
return d[n-1][m-1];
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>g[i][j];
}
}
cout<<bfs()<<endl;
return 0;
}3 Tree and Graph Storage
Number is a special kind of graph (acyclic connectivity graph), which is divided into directed graph and undirected graph according to the Point-Edge relationship between them. An undirected graph can be seen as a special directed graph, which stores two points at a time. Graphs are usually stored in adjacency matrices and adjacency tables, but more often in adjacency tables.
The adjacency matrix g[a, b] stores edges from a to b, and it cannot store overlapping edges. Each single-chain table in the adjacency table represents the points to which each point can reach. The order in the table is irrelevant and header interpolation is used when inserting elements.
ab edge building, initialization-1 means no nodes
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,M=N*2;
int h[N],e[M],ne[M],idx;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int main()
{
memset(h,-1,sizeof h);
return 0;
}4. Traversal of trees and graphs
Because trees are special graphs and graphs are all directed graphs, we only need to know the traversal of directed graphs.
Depth first traverses a road to black
Topic: Center of gravity of trees
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,M=N*2;
int h[N],e[M],ne[M],idx;
bool st[N];
int n;
int ans=N;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx,idx++;
}
int dfs(int u)
{
st[u]=true;
int sum=1,res=0;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
int s=dfs(j);
res=max(res,s);
sum+=s;
}
}
res=max(res,n-sum);
ans=min(res,ans);
return sum;
}
int main()
{
memset(h,-1,sizeof h);
cin>>n;
for(int i=0;i<n-1;i++)
{
int a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout<<ans<<endl;
return 0;
}Width first traversal, suitable for edge length of 1, find the shortest path
Wide search: take the lead, expand, repeat
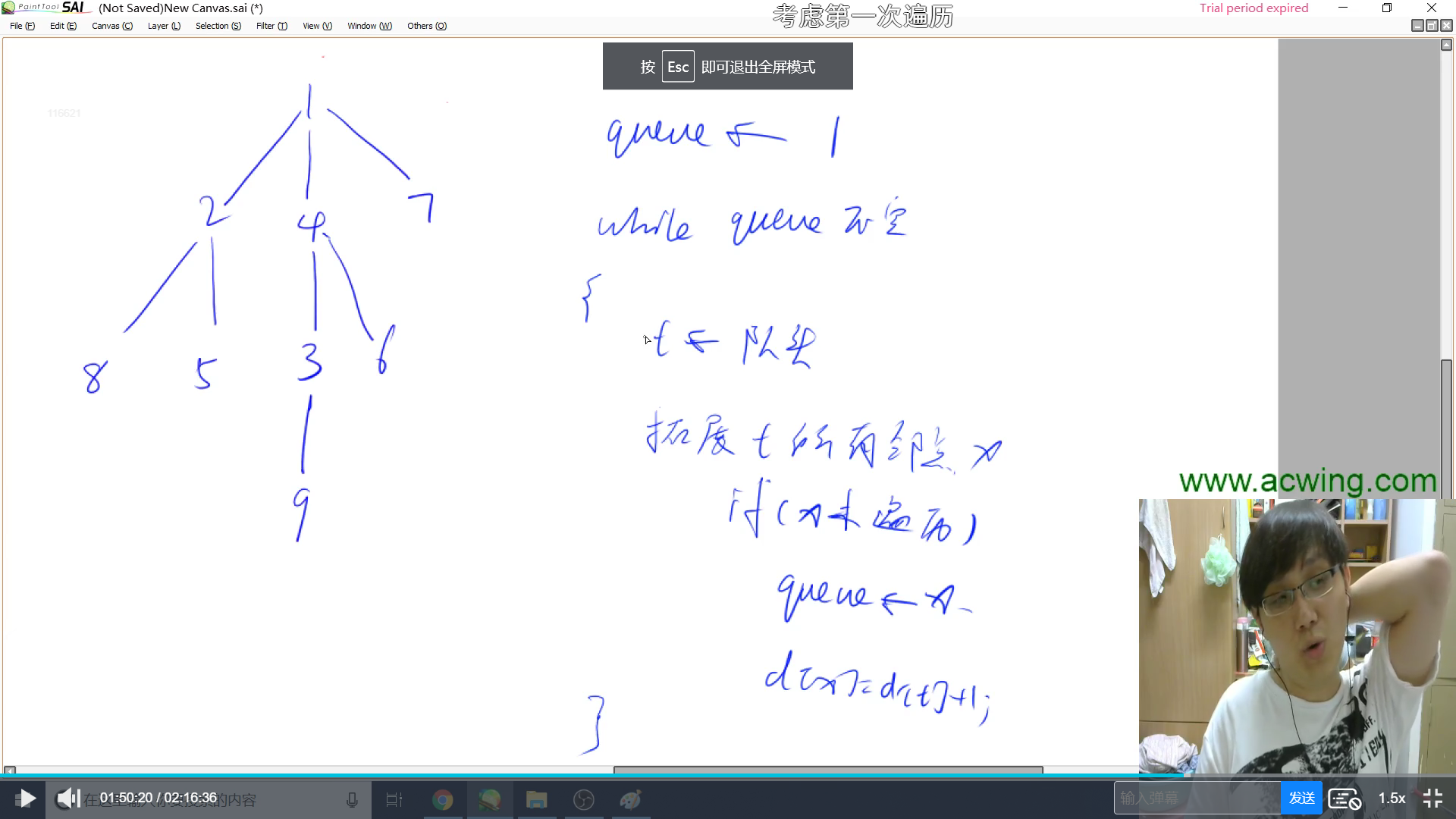
Each time you expand, you just need to look at the edges in your single-chain list.
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx;
int d[N],q[N];
int n,m;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
int hh=0,tt=0;
q[0]=1;
memset(d,-1,sizeof d);
d[1]=0;
while(hh<=tt)
{
int t=q[hh++];
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]==-1)
{
d[j]=d[t]+1;
q[++tt]=j;
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
cout<<bfs()<<endl;
return 0;
}5. Topological sequence of Graphs
For directed graphs, undirected graphs do not have
The values in the topological sequence indicate that all edges are from the number before the sequence to the number after the sequence. Therefore, a directed acyclic graph must have a topological sequence. Each node's degree of entry and exit are recorded, so points with a degree of 0 can be used as starting points.
A directed acyclic graph must have a point with a degree of 0.
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx;
int q[N],d[N];
int n,m;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool topsort()
{
int hh=0,tt=-1;
for(int i=1;i<=n;i++)
{
if(!d[i]) q[++tt]=i;
}
while(hh<=tt)
{
int t=q[hh++];
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
d[j]--;
if(!d[j]) q[++tt]=j;
}
}
return tt==n-1;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
d[b]++;
}
if(topsort())
{
for(int i=0;i<n;i++) cout<<q[i]<<" ";
cout<<endl;
}
else puts("-1");
return 0;
}