A brief introduction of big data types in C language

As we know, there is a limit in the scope of using data types such as int or double to store data directly inside the computer. When the calculation data is large, the computer will overflow, making the calculation result not accurate enough. For example, if a 20 bit decimal integer is stored as an int type variable, data overflow will occur. When the operands are beyond the range of integral type and real type, they must not be directly expressed in the form of a number. In the operation, there are two types of data that can represent large numbers: integer array and string

• Integer array: each element stores one bit, and it needs as many array elements as there are. Each bit is in the form of a number, which can be added and subtracted directly, which is very convenient for operation. However, integer array cannot directly input all elements, but only one input. When inputting, there must be a separator between every two digits, which is not in line with people's habit of inputting values, and the input and output are not square. Then.
• String (essentially an array of characters): the maximum length of a string can represent as many digits as possible. Using string to represent value can input and output all bits directly, but each bit in string is a character, so it must be converted into value for operation, which is not convenient.

Considering the advantages and disadvantages of integer array and character array, in the next problem, we use string to read data, transfer to integer array for operation, and then convert to string for output.

In fact, high-precision operation is to demonstrate the operation steps of simple mathematics on the computer perfectly through programming method.

High precision addition

Problem Description:
Find the sum of two nonnegative integers with no more than 200 bits. Input two lines, each line is a non negative integer with no more than 200 bits, and there is no redundant leading 0; output the calculation formula and the result after adding, and there can be no redundant leading 0 in the result.

Problem analysis:
A string is used to store a value of no more than 200 large integers. Then, for the convenience of operation, the string storing large integers is transferred to the integer array for saving. At the same time, because the two numbers need to be added with the first bit aligned, and then calculated from the low to the high. In fact, when the user inputs, the integer array subscript is 0, which corresponds to the highest bit, while the integer array subscript is the largest, which corresponds to the bit. Therefore, when transferring the string containing the addend to the integer array, the conversion should be reversed first, that is, the integer array subscript is 0, which corresponds to the bit, and the integer array subscript 1 corresponds to ten digits...

#include <stdio.h>
#include <string.h>
#define MAXLEN 210
void Invert(char *a,int *b);//Invert the a character to the integer array b, making sure that the subscript 0 corresponds to the bits instead of the highest bit 
void Output(int *p,int len);//Output integer array elements 
int main(void)
{
 char str1[MAXLEN],str2[MAXLEN],str[MAXLEN];//String containing two addends (input) and (output)
 int a[MAXLEN],b[MAXLEN],c[MAXLEN];//Integer array containing addends and sums (intermediate processing) 
 printf("Enter two addends:\n");
 scanf("%s %s",str1,str2);
 //The elements of integer array a, B and C are all cleared. memset function is generally used to initialize the defined string to "\ 0", which is the fastest way to clear the large structure or array. 
 memset(a,0,sizeof(a));
 memset(b,0,sizeof(b)); 
 memset(c,0,sizeof(c));
 //Store the two plus digit strings in the integer array by bitwise inversion, and the subscript 0 corresponds to one bit.
 Invert(str1,a);
 Invert(str2,b);
 printf("******************Operation process (column addition)******************\n");
 Output(a,strlen(str1));
 printf("\n");
 Output(b,strlen(str2));
 int len=strlen(str1)>=strlen(str2) ? strlen(str1):strlen(str2);//Find the number of digits with a long addend
 for(int i=0;i<len;i++)//Bitwise addition from the first bit to the highest bit 
 {
  c[i]+=a[i]+b[i];
  c[i+1]=c[i]/10;//How many 10 can be divided by c[i] means how many bits can be entered, and the number of I bits can be stored on c[i+1].
  c[i]%=10; //After the completion of c[i], the number is (a[i]+b[i]) modulus 10, which is the remaining number. 
 } 
 printf("\n");
 Output(c,len);
 printf("\n******************Operation process******************");
 while(len>=0&&c[len]==0)//And, remove the leading 0, and copy the result to the string
 {
  len--;
 } 
 memset(str,0,sizeof(str));//0 < = > '\ 0' string Terminator 
 int i=0;
 for(int j=len;j>=0;j--)
 {
  str[i++]=c[j]+'0';//Convert integer numbers to character numbers 
 } 
  if(strlen(str)==0)
 {
  str[0]='0';//Case with result 0 
 }
 printf("\n");
 printf("Operation result:%s + %s = %s\n",str1,str2,str);
 return 0;
} 
void Invert(char *a,int *b)
{
 int len=strlen(a),j=0;
 for(int i=len-1;i>=0;i--)
 {
  b[j++]=a[i]-'0';
 }
}
void Output(int *p,int len)
{
 for(int i=0;i<len;i++)
 {
  printf("%d",p[i]);
 }
}

Operation output: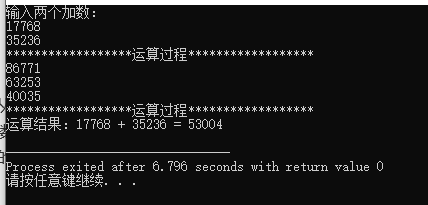

Code explanation:
How to calculate integer array? That is, to simulate the vertical addition method of primary school students, align the bits, add from the bits to the corresponding bits of the high bit by bit, and carry if the sum is greater than or equal to 10. In the following source code, use int a[210] to save the first addend, int b[210] to save the second addend, and then add them bit by bit. The result of adding the two numbers is stored in int c[210], where the following code segment deals with carry case.

 for(int i=0;i<len;i++)//Bitwise addition from the first bit to the highest bit 
 {
  c[i]+=a[i]+b[i];
  c[i+1]=c[i]/10;//How many 10 can be divided by c[i] means how many bits can be entered, and the number of I bits can be stored on c[i+1].
  c[i]%=10; //After the completion of c[i], the number is (a[i]+b[i]) modulus 10, which is the remaining number. 
 } 

High precision multiplication

Problem Description:
Find the product of two large integers of no more than 1000 bits. Input two lines, each line is an integer of no more than 1000 bits, without redundant leading 0; output the formula and the result after multiplication. There cannot be any extra leading zeros in the result.

Problem analysis:
Here, we need to consider the sign for multiplication and the data structure is unchanged. We only need to consider the simulation process of changing the algorithm to multiplication operation: