1, Multiple choice questions

1. A. basic questions. Check the computer hardware system. The core of the computer host includes memory and processor. It will not start without memory
2. B. the queue is a first in first out linear table
3. A. basic questions, review computer knowledge
4. B. basic question. Check the binary conversion. The binary representation of 9A is 1001 1010, and the conversion to octal is 232
5. C, basic questions, investigate the basis of computer, common operating system, C is graphics processing software, is application software
6. C. data structure problem. Check the traversal of binary tree. If option C is selected, it is impossible to determine the binary tree. It is contradictory
7. B. basic questions, common CPU
8. C. algorithm problem, investigate the bubble sorting algorithm. Bubble sorting is to compare two adjacent elements each time, and each exchange is also to exchange two adjacent elements, so each exchange only reduces one reverse pair, and the number of reverse pairs in the enumeration sequence is 10
9. A. basic questions, general knowledge of computer history
10,A
11. B. basic questions, review the related concepts of computer foundation, multimedia technology and vector graph
12. D. data structure problem, investigate the out stack and in stack sequence of the stack, and substitute into the option simulation to get D
13. B. basic questions, review the basics of computer network, browser
14. C. basic questions, review common application layer protocols of computer networks, e-mail service protocols, POP3
15. C. algorithm problem, investigate the basic concepts of divide and conquer algorithm
16. D. basic questions: check the knowledge of computer hardware, CPU address bus and addressing space. Theoretically, the addressing space is equal to the maximum range of binary data that can be represented by the bus length, 32-bit bus, i.e. 2^32=4G
17. C. basic questions: computer network, WLAN, Bluetooth and wifi are common WLAN devices
18. A. the basic problem is to investigate the implementation of recursive programs. The recursive execution process of recursive programs is realized by the stack allocated by the operating system. If there are too many recursive layers, it will cause stack space overflow
19. C, basic questions, enumeration can get 1 + 2 +... + 9-32-31 = 36
20. B. basic questions, scientific knowledge

2, Problem solving

1. The abscissa and ordinate of each integral point are integers, either odd or even. There are only four cases (odd, even), (even, odd), (odd, odd) and (even, even). Assuming that the coordinates of any two points are (x1,y1),(x2,y2) respectively, the coordinates of the midpoint of the connecting line are ((x1+x2)/2, (y1+y2)/2), except that (odd + even) cannot be divided by 2, Other combinations can be divided by 2. Obviously, the midpoint of any two of the four coordinates (odd, even), (even, odd), (odd, odd), (even, even) is not the whole point. Then add any of the four coordinates, such as (even, even), and you can find that at least two points are the whole point, so the answer is 5

2. Combinatorial math problems, first specify a type of 5 players to make a circular arrangement, such as 5 mainland players, with a circular arrangement of 5/ 4 = 24 kinds, each arrangement has 5 spaces, which can be used to insert 5 Hong Kong and Macao players, a total of 5! According to the principle of multiplication, there are 24 insertion methods in total × 5!= 2880 species

3, Reading program

1,

#include <iostream>
using namespace std;
int a,b,c,d,e,ans;
int main()
{
    cin>>a>>b>>c;
    d=a+b;
    e=b+c;
    ans=d+e;
    cout<<ans<<endl;
    return 0;    
}

Programming questions can be directly substituted into the input, and the result is 10

2,

#include <iostream>
using namespace std;
int n,i,ans;
int main()
{
    cin>>n;
    ans=0;
    for(i=1;i<=n;i++)
        if(n%i==0) ans++;
    cout<<ans<<endl;
    return 0;    
}

Find the number of divisors of 18 and enumerate them in turn to get: 1, 2, 3, 6, 9, 18, 6 in total

3,

#include <iostream>
using namespace std;
int n,i,j,a[100][100];
int solve(int x,int y)
{
    int u,v;
    if(x==n) return a[x][y];
    u=solve(x+1,y);
    v=solve(x+1,y+1);
    if(u>v) return a[x][y]+u;
    else return a[x][y]+v;    
}
int main()
{
    cin>>n;
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++) cin>>a[i][j];
    cout<<solve(1,1)<<endl;
    return 0;    
}

Investigate the recursive function solution and print the table to get the result 14

4,

#include <iostream>
#include <string>
using namespace std;
int n,i,j,ans;
string s;
char get(int i)
{
    if(i<n) return s[i];
    else return s[i-n];    
}
int main()
{
    cin>>s;
    n=s.size();
    ans=0;
    for(i=1;i<=n-1;i++)
    {
        for(j=0;j<=n-1;j++)
            if(get(i+j)<get(ans+j))
            {
                ans=i;
                break;    
            }
            else if(get(i+j)>get(ans+j)) break;
    }
    for(j=0;j<=n-1;j++) cout<<get(ans+j);
    cout<<endl;
    return 0;    
}

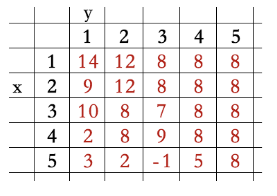
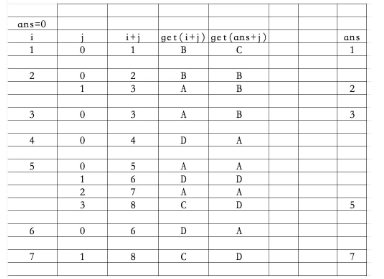
First, list the value list of get(i), and call the get(i) function many times in the code

Then print the table to get ans=7, then output get(ans+j), and output get(7)-get(14), which is acbbad

3, Perfect procedure

1. (coordinate Statistics) enter the coordinates of n whole points on the plane. For each point, it can control all the points located at the lower left (that is, the x and y coordinates are smaller than it). The number of points it can control is called "combat effectiveness". Output the combat effectiveness of each point in turn, and finally output the number of the point with the highest combat effectiveness (if the combat effectiveness of several points is the highest in parallel, output the largest number).

#include <iostream>
using namespace std;
const int SIZE =100;
int x[SIZE],y[SIZE],f[SIZE];
int n,i,j,max_f,ans;
int main()
{
    cin>>n;
    for(i=1;i<=n;i++) cin>>x[i]>>y[i];
    max_f=0;
    for(i=1;i<=n;i++)
    {
        f[i]= [  ①   ];
        for(j=1;j<=n;j++)
        {
            if(x[j]<x[i] && [   ②    ])
            [      ③      ] ;
        }
        if( [     ④       ])
        {
            max_f=f[i];
            [    ⑤    ];    
        }
    }
    for(i=1;i<=n;i++) cout<<f[i]<<endl;
    cout<<ans<<endl;
    return 0;    
}

Simple simulation algorithm, count the combat effectiveness of each point in turn, and compare the points with the maximum combat effectiveness. If they are the same, take the latest one, that is, the one with the highest number
① 0. The initial combat effectiveness is 0
② y[j]<y[i]
③ f[i]++
④ f[i]>=max_f
⑤ ans = i

2. (number of permutations) input two positive integers n, m (1 < n < 20,1 < m < n), take any number of m in 1~n, and output all such permutations from small to large in dictionary order. For example:
Input: 3 2
Output:
1 2
1 3
2 1
2 3
3 1
3 2

#include <iostream>
#include <cstring>
using namespace std;
const int SIZE =25;
bool used[SIZE];
int data[SIZE];
int n,m,i,j,k;
bool flag;
int main()
{
    cin>>n>>m;
    memset(used,false,sizeof(used));
    for(i=1;i<=m;i++)
    {
        data[i]=i;
        used[i]=true;    
    }
    flag=true;
    while(flag)
    {
        for(i=1;i<=m-1;i++) cout<<data[i]<<" ";
        cout<<data[m]<<endl;
        flag= [    ①    ] ;
        for(i=m;i>=1;i--)
        {
            [    ②     ];
            for(j=data[i]+1;j<=n;j++)
                if(!used[j])
                {
                    used[j]=true;
                    data[i]=[    ③  ] ;
                    flag=true;
                    break;    
                }
            if(flag)
            {
                for(k=i+1;k<=m;k++)
                    for(j=1;j<= [   ④   ];j++)
                    if(!used[j])
                    {
                        data[k]=j;
                        used[j]=true;
                        break;
                    }
                [     ⑤   ];
            }
        }
    }
    return 0;    
}

The example given in the project is too weak. The usual n numbers are arranged in m numbers and output according to the size order of the dictionary. As shown in the figure, we enumerate in order. Each time, we need to find the first number that can be increased from right to left. For example, Ax can be increased to Ay, and then we need to re sort the numbers on the right of Ay according to the size order and enumerate them in order.
For example, if n = 5 and M = 4, the first arrangement must be 1, 2, 3 and 4. Then, starting from the right, the first 4 can only become 5. Row 5 and release 4 at the same time. At this moment, there are no numbers on the right side of 5. Continue to the next round, the first number that can be increased is 3, increase 3 to 4, release 3 at the same time, and then there is a digit on the right of 3. This number will be selected and arranged from the remaining non arranged numbers in order from small to large, that is, 3, 5, and so on, until the enlargement of each number that can be increased is experienced from right to left.

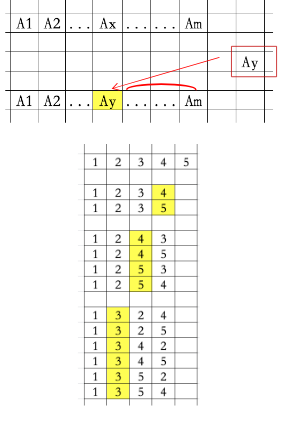
The first part of the while loop is to output the currently found permutation
① False, flag indicates whether a valid permutation is currently found. The initial value is false, ② used[data[i]]=false. Find a larger number to replace from right to left. First release the data[i] to be replaced, and then select the first unselected number row from data[i]+1 to n and put it on position I of data[i], ③ j. at this moment, set flag to true, indicating that a new permutation scheme is found, Then, if there are still numbers on the right side of I, fill in the position on the right side of I, i.e. i+1 to m, with the remaining unselected numbers in order from small to large. ④ n and ⑤ break jump out of the cycle, directly enter the head of the next outer while cycle, and output the arrangement scheme found in the previous round.