1, Multiple choice questions

1. B. basic problem, investigate binary operation
2. B, basic question, 48 + 9 = 57
3. C, basic questions, storage space calculation, 8GB/2MB=8*1024/2=4096
4. C, basic questions, basic computer knowledge, Moore's law
5. B. according to the meaning of the question, any two of the seven vertices have exactly one edge, which is the combination number of two out of seven, 21
6. D. basic questions, investigate the computer hardware system, CPU composition and registers
7. C, data structure problem, calculation of binary tree node points, when the depth is the least, it must be a complete binary tree, and the leaf node of the full binary tree with depth n is 2 n − 1 2^{n-1} 2n − 12011 is closest to 2048, i.e 2 11 2^{11} 211, so n-1=11,n=12
8. B. algorithm problem, investigate the basic idea of insertion sorting
9. C, basic question, check binary conversion, binary to hexadecimal, every 4 bits of binary to 1 bit of hexadecimal, 100 / 4 = 25
10. C. basic questions, examine the common sense of computer file deletion
11. B. data structure problem, investigate the application of BFS and queue
12. A, algorithm problem, investigate the concept of spatial complexity
13. C, data structure questions, linked lists can not be accessed randomly, but can only be traversed in sequence
14. C. basic questions, Fundamentals of Informatics, common sense of mainstream technology application, ABD all have biological characteristics, C does not
15. C, data structure problem, investigate the Huffman tree, and construct the Huffman tree according to the Huffman algorithm to get C
16. D. basic questions, investigation of programming language, assembly language, assembly language are widely used in lower level development and application, and have not been eliminated
17. A, algorithm problem, investigate the basic concepts of backtracking algorithm
18. A. basic questions, common sense of computer history
19. A, data structure problem, investigate the connectivity of the graph, enumerate each option in turn, and find out whether each edge has other paths to replace. Only edge a has alternative paths
20. C. basic questions, investigation of computer history, the core content of von Neumann's computer architecture, using the principle of stored program and program control

2, Problem solving

1. In math problems, in all sequences, the number of 1 is either even or odd, so each accounts for half, so it is the full arrangement of 8 divided by 2128

2. Editing distance can be done by dynamic programming algorithm, but the sequence given in this question is relatively simple and can be observed directly. 1. Delete A to get BCDEFG
2. Replace C with A to get BADEFG
3. Replace F with C to get BADECG
3 steps in total

3, Reading program

1,

#include<iostream>
using namespace std;

int main()
{
    int i,n,m,ans;
    cin>>n>>m;
    i=n;
    ans=0;
    while(i<=m){
       ans+=i;
       i++;
    }
    cout<<ans<<endl;
    return 0;
}

Input: 10 20
Simple programming problem, investigate the while loop statement, the function of the code is to calculate the sum accumulated from 10 to 20, and the result is 165

2,

#include<iostream>
#include<string>
using namespace std;

int main()
{
    string map= "2223334445556667778889999";
    string tel;
    int i;
    cin>>tel;
    for(i=0;i<tel.length();i++)
       if((tel[i]>='0') && (tel[i]<='9') )
           cout<<tel[i];
       else if( (tel[i]>='A') && (tel[i]<='Z'))
           cout<<map[tel[i]-'A'];
    cout<<endl;
    return 0;
}

Input: CCF-NOIP-2011
Simple programming problem, investigating string traversal and processing, the result is: 22366472011

3,

#include<iostream>
#include<cstring>
using namespace std;

const int SIZE = 100;

int main()
{
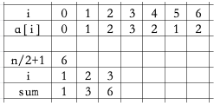
    int n,i,sum,x,a[SIZE];

    cin>>n;
    memset(a,0,sizeof(a));

    for(i=1;i<=n;i++){
        cin>>x;
        a[x]++;
    }
    i=0;
    sum=0;
    while(sum<(n/2+1)){
        i++;
        sum+=a[i];
    }
    cout<<i<<endl;
    return 0;
}

Input:
11
4 5 6 6 4 3 3 2 3 2 1
For programming questions, the output i is 3

4,

#include<iostream>
using namespace std;

int solve(int n,int m)
{
    int i,sum;
    if(m==1) return 1;
    sum=0;
    for(i=1;i<n;i++)
       sum+= solve(i,m-1);
    return sum;
}

int main()
{
    int n,m;
    cin>>n>>m;
    cout<<solve(n,m)<<endl;
    return 0;
}

Input: 7 4

Solve the problem recursively. Read the recursive logic of the solve function. When m=1, return 1. Otherwise, the value of solve(n,m) is equal to solve(1,m-1)+solve(2,m-1) +... + solve(n-1,m-1). If you print the table, you can get the result of 20

4, Perfect procedure

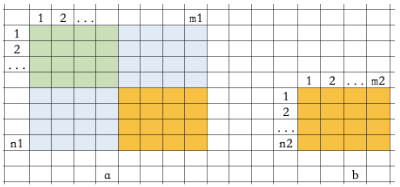
1. (submatrix) input a matrix A of n1m1 and a matrix b of n2m2, and ask whether there is a submatrix in a that is equal to b. If it exists, output the coordinates of the upper left corner of all sub matrices; if it does not exist, output "There is no answer".

#include<iostream>
using namespace std;

const int SIZE = 50;

int n1,m1,n2,m2,a[SIZE][SIZE],b[SIZE][SIZE];


int main()
{
    int i,j,k1,k2;
    bool good ,haveAns;

    cin>>n1>>m1;
    for(i=1;i<=n1;i++)
       for(j=1;j<=m1;j++)
          cin>>a[i][j];

    cin>>n2>>m2;
    for(i=1;i<=n2;i++)
       for(j=1;j<=m2;j++)
           [   ①     ];

    haveAns=false;
    for(i=1;i<=n1-n2+1;i++)
       for(j=1;j<= [    ②     ];j++){
            [   ③    ];
           for(k1=1;k1<=n2;k1++)
               for(k2=1;k2<=[    ④    ] ;k2++){
                  if(a[i+k1-1][j+k2-1]!=b[k1][k2])
                     good=false;
               }
          if(good){
             cout<<i<<' '<<j<<endl;
             [       ⑤      ];
          }
       }
    if(!haveAns)
       cout<<"There is no answer"<<endl;

    return 0;
}

If there is a submatrix equal to b in a, as shown in the figure, the upper left corner coordinates of the submatrix equal to b in a can only move in the green matrix area, so traverse each coordinate in the area to judge whether the submatrix whose size is equal to b is equal to b.
①cin>>b[i][j]
② m1-m2+1, width of green area
③ good=true, set the initial value of good
④ m2, compare whether each element of the submatrix is equal to the element corresponding to b
⑤ hasAns=true, find a submatrix equal to b

2. (large integer square) enter a positive integer n (1 ≤ n ≤ 10 ^ 100), and try the dichotomy to calculate the integer part of its square root.

#include<iostream>
#include<string>
using namespace std;

const int SIZE=200;
struct hugeint{
    int len,num[SIZE];
};
//Where len represents the number of bits of a large integer; num[1] represents one bit, num[2] represents ten bits, and so on

hugeint times(hugeint a,hugeint b)
// Calculates the product of large integers a and b
{
    int i,j;
    hugeint ans;
    memset(ans.num,0,sizeof(ans.num));
    for(i=1;i<=a.len;i++)
       for(j=1;j<=b.len;j++)
            [      ①     ] +=a.num[i]*b.num[j];  
    for(i=1;i<=a.len+b.len;i++){
        ans.num[i+1]+=ans.num[i]/10;
        [         ②         ]; 
    }
    if(ans.num[a.len+b.len]>0)
        ans.len=a.len+b.len;
    else
        ans.len=a.len+b.len-1;
    return ans;
}

hugeint add(hugeint a,hugeint b)
//Calculate the sum of large integers a and b
{
    int i;
    hugeint ans;
    memset(ans.num,0,sizeof(ans.num));
    if(a.len>b.len)
        ans.len=a.len;
    else
        ans.len=b.len;
    for(i=1;i<=ans.len;i++){
        ans.num[i]+= [        ③      ] ; 
        ans.num[i+1]+= ans.num[i]/10;
        ans.num[i]%=10;
    }
    if(ans.num[ans.len+1]>0)
        ans.len++;
    return ans;
}

hugeint average(hugeint a,hugeint b)
//Calculates the integer part of the average of large integers a and b
{
    int i;
    hugeint ans;
    ans=add(a,b);
    for(i=ans.len;i>=2;i--){
        ans.num[i-1]+=([     ④      ])*10; 

        ans.num[i]/=2;
    }
    ans.num[1]/=2;
    if(ans.num[ans.len]==0)
        ans.len--;
    return ans;
}

hugeint plustwo(hugeint a)
// Calculates the result of a large integer a plus 2
{
    int i;
    hugeint ans;
    ans=a;
    ans.num[1]+=2;
    i=1;
    while( (i<=ans.len)&&(ans.num[i]>=10) ){
        ans.num[i+1]+=ans.num[i]/10;
        ans.num[i]%=10;
        i++;
    }
    if(ans.num[ans.len+1]>0)
        [      ⑤    ]; 
    return ans;
}

bool over(hugeint a,hugeint b)
// If the large integer a > b, it returns true; otherwise, it returns false
{
    int i;
    if([      ⑥     ])  
        return false;
    if( a.len>b.len )
        return true;
    for(i=a.len;i>=1;i--){
        if(a.num[i]<b.num[i])
           return false;
        if(a.num[i]>b.num[i])
           return true;
    }
    return false;
}

int main()
{
    string s;
    int i;
    hugeint target,left,middle,right;
    cin>>s;
    memset(target.num,0,sizeof(target.num));
    target.len=s.length();
    for(i=1;i<=target.len;i++)
        target.num[i]=s[target.len-i]-[      ⑦    ];
    memset(left.num,0,sizeof(left.num));
    left.len=1;
    left.num[1]=1;
    right=target;
    do{
        middle=average(left,right);
        if(over([       ⑧        ]))
            right=middle;
        else
            left=middle;
    }while(!over(plustwo(left),right) );
    for(i=left.len;i>=1;i--)
       cout<<left.num[i];
    return 0;
}

For the application of high-precision operation, the code is long and there are many functions. After reading, it is found that they are common functions for high-precision operation, such as multiplication, addition, etc.
① ans.num[i+j-1], subscript of high-precision multiplication result array
② ans.num[i]%=10, carry from low to high, and take the remainder from low
High precision addition, bitwise addition
③ a.num[i]+b.num[i]
High precision divided by low precision, here is divided by constant 2
④ ans.num[i]%2
High precision plus low precision
⑤ ans.len + +, the highest bit generates a new carry, and the total length is added by 1
Compare the size of two high-precision numbers
⑥ A. len < b.len, compare the length first. If the length is small, the value must be smaller
⑦ '0' or 48, convert the number in the input string format into a high-precision character array storage mode. Note that it is in reverse order
Then use the dichotomy to approximate and solve the square root. Take the midpoint value each time to judge whether the square of the middle is greater than the original number. If it is greater than, it means that it is larger. You need to continue to find it on the left, otherwise you need to continue to find it on the right
⑧ times(middle, middle), target

The code of this question is very long, but it is actually less difficult. In addition to the two blanks 7 and 8 in the main function, the basic operations of high-precision operation are in front. The answers can be found in the corresponding function code.