Title Description
Linux users and OSX users must be familiar with package manager. Through the package manager, you can install a package through a line of commands, and then the package manager will help you download the package from the software source, and automatically solve all the dependencies (that is, download and install other packages that the installation of this package depends on), and complete all the configurations. Apt get for Debian/Ubuntu, yum for Fedora/CentOS, and homebrew for OSX are excellent package managers.
You decide to design your own package manager. Inevitably, you have to solve the problem of dependencies between packages. If package a relies on package B, package B must be installed before package a can be installed. At the same time, if you want to uninstall package B, you must uninstall package a. Now you have all the dependencies between packages. Moreover, due to your previous work, except for package 0, all packages in your manager will depend on one and only one package, while package 0 does not depend on any one package. There is no ring (if there are m(m ≥ 2) packages A1,A2,A3,..., Am, where a1 depends on A2, A2 depends on A3, A3 depends on A4,... A[m-1] depends on Am, and Am depends on A1, which is called the dependency of these m software packages to form a ring). Of course, there will not be a software package dependent on itself.
Now you write a dependency solution for your package manager. According to the feedback, users want to quickly know how many packages the operation will actually change when installing and uninstalling a package (that is, how many packages are not installed during the installation operation, or how many installed packages are uninstalled during the uninstallation operation). Your task is to realize this part. Note that installing an installed package or uninstalling an uninstalled package will not change the installation status of any package, that is, in this case, the number of packages that change the installation status is 0.
Input format
Read in the data from the file manager.in.
Line 1 of the input file contains an integer n representing the total number of packages. Packages are numbered from 0.
The next line contains n − 1 integers, separated by a single space between adjacent integers, representing the number of packages that package 1, 2, 3,..., n − 2,n − 1 depends on.
The next line contains an integer q, which represents the total number of queries. Then line q, one query per line. There are two types of inquiry:
install x: indicates to install package x
uninstall x: indicates to uninstall package x
You need to maintain the installation status of each package. At the beginning, all packages are not installed.
For each operation, you need to output how many packages the operation will change the installation status, and then apply the operation (that is, change the installation status you maintain).
Output format
Output to the file manager.out.
The output file includes line q.
Output an integer in line i of the output file, which is the number of packages changing the installation status in step i.
Example of input and output
Enter "copy 1"
7 0 0 0 1 1 5 5 install 5 install 6 uninstall 1 install 4 uninstall 0
Output 1 copy
3 1 3 2 3
Enter 2 copy
10 0 1 2 1 3 0 0 3 2 10 install 0 install 3 uninstall 2 install 7 install 5 install 9 uninstall 9 install 4 install 1 install 9
Output 2 copy
1 3 2 1 3 1 1 1 0 1
Description / tips
[example 1]
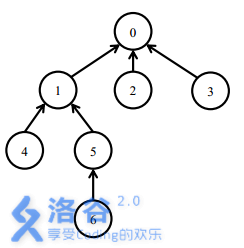
At first, all the packages were not installed.
To install package 5, you need to install three packages: 0, 1 and 5.
Then install package 6. You only need to install package 6. Four packages 0,1,5,6 are installed.
To uninstall package 1, you need to uninstall package 1, 5 and 6. At this time, only package 0 is still installed.
Then install package 4. You need to install package 1 and package 4. 0,1,4 are now installed. Finally, uninstalling package 0 uninstalls all packages. `
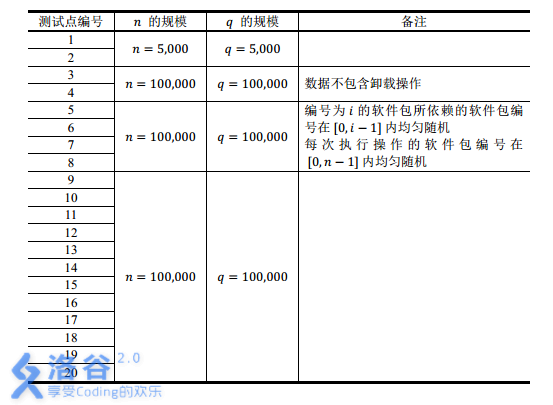
[data range]
[time limit 1s, memory 512M]
Understanding of tree building after tree cutting
The basis of tree chain segmentation is not mentioned. Tree building and query is to take a heavy chain or light chain as an interval to find distance (the heavy chain and light chain are continuous after tree segmentation), so as to speed up query speed.
thinking
Unload: calculate the downloaded points in the subtree with this point as the root node, that is, query quary2 (ID [x], ID [x] + size [x] - 1, 1)
[ID [x], ID [x] + size [x] - 1] is the interval of X subtree.
Download: the number of downloaded points on the path from the root to the point is calculated, and then the number is subtracted by the depth of the point, that is, ans_i = dep [x] - sum1
Code
Digestion and understanding, tree dissection...
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <map>
#define N 100005
using namespace std ;
int n , m , ans ;
int dep[N] , fa[N] , son[N] , Size[N] ;
int top[N] , id[N] , be[N] , cnt ;//DFS sequence with id as point x, be as the corresponding point of DFS sequence
vector <int> G[N] ;
struct node {
int l , r , sum ;
int lazy ;
} Tree[4*N] ;
void pushup( int x ) {//To update
int lson = 2*x , rson = 2*x+1 ;
Tree[x].sum = Tree[lson].sum + Tree[rson].sum ;
}
void pushdown( int x ) {//Drop lazy flag
if( Tree[x].lazy == 1 ) {
Tree[x].lazy = 0 ;
Tree[x*2].sum = Tree[x*2].r-Tree[x*2].l+1 ;
Tree[x*2+1].sum = Tree[x*2+1].r-Tree[x*2+1].l+1 ;//Update left and right sons
Tree[x*2].lazy = Tree[x*2+1].lazy = 1 ;
return ;
}
if( Tree[x].lazy == 2 ) {
Tree[x].lazy = 0 ;
Tree[x*2].sum = Tree[x*2+1].sum = 0 ;//Update left and right sons
Tree[x*2].lazy = Tree[x*2+1].lazy = 2 ;
}
}
void build( int l, int r , int x ) {//Line segment tree
if( l == r ) {
Tree[x].lazy = 0 ;
Tree[x].l = Tree[x].r = l ;
Tree[x].sum = 0 ;
return ;
}
Tree[x].sum = 0 , Tree[x].lazy = 0 ;
Tree[x].l = l , Tree[x].r = r ;
int mid = (l+r)/2 ;
build(l,mid,x*2);
build(mid+1,r,x*2+1);
pushup(x) ;
}
int quary1( int l , int r , int x ) {//download
if( l > r )
swap(l,r) ;
if( l <= Tree[x].l && r >= Tree[x].r ) {
int sum = Tree[x].sum ;
Tree[x].sum = Tree[x].r-Tree[x].l+1 ;//Download assignment
Tree[x].lazy = 1 ;//Lazy mark
return sum ;
}
int mid = (Tree[x].l+Tree[x].r)/2 ;
pushdown(x) ;//Drop lazy flag
int sum = 0 ;
if( l <= mid )
sum += quary1(l,r,x*2) ;
if( r >= mid+1 )
sum += quary1(l,r,2*x+1) ;
pushup(x) ;//To update
return sum ;
}
int quary2( int l , int r , int x ) {//uninstall
if( l > r )
swap(l,r) ;
if( l <= Tree[x].l && r >= Tree[x].r ) {
int sum = Tree[x].sum ;
Tree[x].sum = 0 ;//Unload cleared
Tree[x].lazy = 2 ;//Lazy mark
return sum ;
}
int mid = (Tree[x].l+Tree[x].r)/2 ;
pushdown(x);//Drop lazy flag
int sum = 0 ;
if( l <= mid )
sum += quary2(l,r,x*2) ;
if( r >= mid+1 )
sum += quary2(l,r,2*x+1) ;
pushup(x) ;//To update
return sum ;
}
void DFS1( int x , int f , int deep ) {
fa[x] = f ;
dep[x] = deep ;
Size[x] = 1 ;
for( int i = 0 ; i < G[x].size() ; ++ i ) {
int s = G[x][i] ;
if( s == f )
continue;
DFS1( s,x,deep+1 );
Size[x] += Size[s] ;
if( Size[s] > Size[son[x]] || !son[x] )
son[x] = s ;
}
}
void DFS2( int x , int T ) {
top[x] = T ;
cnt ++ ;
id[x] = cnt ;
be[cnt] = x ;
if( !son[x] )
return ;
DFS2( son[x] , T );
for( int i = 0 ; i < G[x].size() ; ++ i ) {
int s = G[x][i] ;
if( s == son[x] || s == fa[x] )
continue ;
DFS2(s,s);
}
}
int Get_sum( int x , int y ) {
int sum = 0 ;
while( top[x] != top[y] ) {
if( dep[x] < dep[y] )
swap(x,y) ;
sum += quary1( id[x],id[top[x]],1 );
x = fa[top[x]] ;
}
sum += quary1( id[x],id[y],1 );
return sum ;
}
int main() {
scanf("%d", &n );
for( int i = 1 ; i < n ; ++ i ) {
int x ;
scanf("%d", &x );
G[i].push_back(x) ;
G[x].push_back(i) ;
}
cnt = 0 ;
DFS1(0,-1,1);
DFS2(0,0) ;
build(1,n,1);
scanf("%d", &m );
while( m -- ) {
string Fuck ;
cin >> Fuck ;
int x ;
scanf("%d", &x );
if( Fuck[0] == 'i' ) {
ans = Get_sum(x,0);
printf("%d\n", dep[x]-ans );
}
else {
ans = quary2( id[x] , id[x]+Size[x]-1 , 1 );
printf("%d\n", ans ) ;
}
}
}