nn.Conv2d -- two dimensional convolution operation

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

Function: 2D convolution operation is applied to the input signal composed of multiple input planes, which is commonly used in image processing.

Input:

• in_channels: enter the number of channels in the image
• out_channels: the number of channels generated by convolution operation
• kernel_size: convolution kernel size, integer or tuple type
• Stripe: the stride of convolution operation, integer or tuple type. The default is 1
• Padding: padding size at the boundary, integer or tuple type, 0 by default
• padding_mode: filling method, zeros, reflect, replicate, circular. Zeros is the default
  zeros: zero filling, all filling 0 at the tensor boundary
  reflect: Mirror filling, which takes the edge of the matrix as the axis of symmetry and fills the symmetrical elements in the opposite direction to the outermost.
  replicate: copy filling, filling the tensor with the copy value of the input boundary
  circular: circular filling, repeating elements on the other side of the matrix boundary
  See code cases for specific differences
• Division: the distance between control points. The default is 1. If it is greater than 1, the operation is also called expansion convolution operation.
  A graph to understand the extended convolution operation

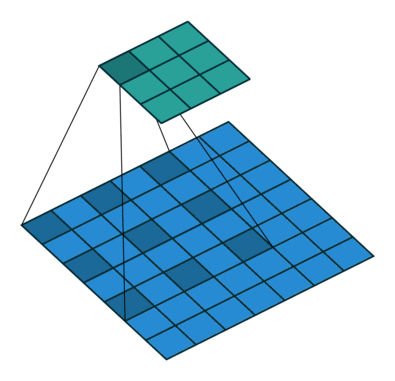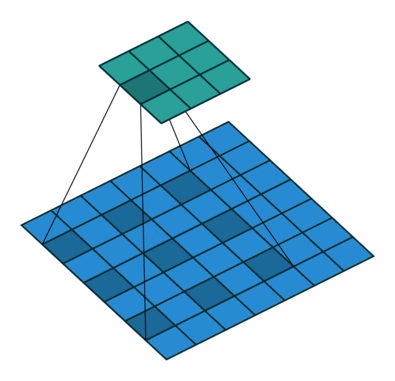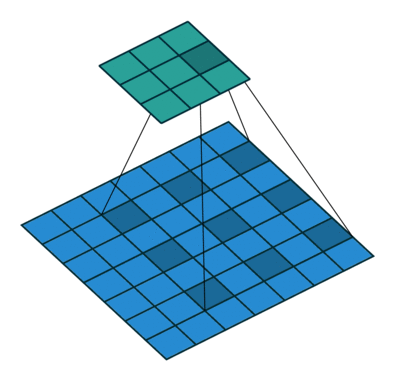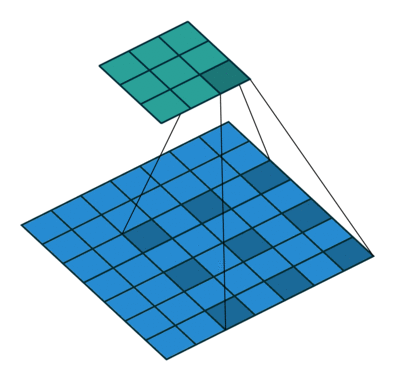
Image source: https://github.com/vdumoulin/conv_arithmetic

• groups: controls the connection between input and output. The default is 1.
  • When groups=1, all inputs are convoluted into outputs
  • When groups=2, this operation is equivalent to first halving the input channel, respectively through the same conv operation (so the convolution parameters will be halved), generating the corresponding output, and then connecting the two outputs. Groups > 2 is similar, and the maximum number of input channels cannot be exceeded.
  • groups must be divisible by in_channels and out_channels
• bias: whether there is an offset item. The default is True, that is, there is an offset item by default.
• The array data type entered must be TensorFloat32

be careful:

• in_channels, out_channels and kernel_size is a parameter that must be specified. Other parameters have default values and can not be specified.
• kernel_size, stripe, padding, and division can be specified as either integer or tuple types.
  • If specified as an integer, the height and width dimensions use the same value (square)
  • If it is specified as a tuple type, the first value in the tuple is used for height and the second dimension is used for width (rectangle)

Supplement:

• Calculation formula of height and width of output image (the formula is transferred from the official document):

KAtex parse error: expected 'EOF', got '&' at position 8: assumption: \ \& ̲ Input: (n, C #u{i

H o u t = H i n + 2 × p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] × ( k e r n e l _ s i z e [ 0 ] − 1 ) − 1 s t r i d e [ 0 ] + 1 W o u t = W i n + 2 × p a d d i n g [ 1 ] − d i l a t i o n [ 1 ] × ( k e r n e l _ s i z e [ 1 ] − 1 ) − 1 s t r i d e [ 1 ] + 1 H_{out}=\frac{H_{in}+2\times padding[0]-dilation[0]\times(kernel\_size[0]-1)-1}{stride[0]}+1\\ W_{out}=\frac{W_{in}+2\times padding[1]-dilation[1]\times(kernel\_size[1]-1)-1}{stride[1]}+1\\ Hout​=stride[0]Hin​+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1​+1Wout​=stride[1]Win​+2×padding[1]−dilation[1]×(kernel_size[1]−1)−1​+1

• The weight of the convolution layer can be extracted by the method Conv2d.weight, and the output weight array size is:
  ( o u t _ c h a n n e l s , i n _ c h a n n e l s g r o u p s , k e r n e l _ s i z e [ 0 ] , k e r n e l _ s i z e [ 0 ] ) (out\_channels,\frac{in\_channels}{groups},kernel\_size[0],kernel\_size[0]) (out_channels,groupsin_channels​,kernel_size[0],kernel_size[0])

And the initialization weight division obeys uniform distribution:
u ( − k , k ) , his in k = g r o u p s C i n × ∏ i = 0 1 k e r n e l _ s i z e [ i ] u(-\sqrt{k},\sqrt{k}), where k = \ frac {groups} {C {in} \ times \ prod \ limits {I = 0} ^ 1 kernel \ _size [i]} u(−k ​,k ), where k=Cin × i=0∏1​kernel_size[i]groups​

• The offset parameters of the convolution layer can be extracted by the method Conv2d.bias (assuming bias=True). The output array size is the same as the out_channels size, and the initialization part is the same as the weight part.
• Convolution layer parameters can also be obtained through the. parameters() method

Code case

General usage

import torch.nn as nn
import torch
img=torch.arange(49,dtype=torch.float32).view(1,1,7,7)
conv=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3)
img_2=conv(img)
print(img)
print(img_2)

output

# Before convolution
tensor([[[[ 0.,  1.,  2.,  3.,  4.,  5.,  6.],
          [ 7.,  8.,  9., 10., 11., 12., 13.],
          [14., 15., 16., 17., 18., 19., 20.],
          [21., 22., 23., 24., 25., 26., 27.],
          [28., 29., 30., 31., 32., 33., 34.],
          [35., 36., 37., 38., 39., 40., 41.],
          [42., 43., 44., 45., 46., 47., 48.]]]])
# After convolution
tensor([[[[4.7303, 4.8851, 5.0398, 5.1945, 5.3492],
          [5.8134, 5.9681, 6.1228, 6.2775, 6.4323],
          [6.8964, 7.0512, 7.2059, 7.3606, 7.5153],
          [7.9795, 8.1342, 8.2889, 8.4436, 8.5984],
          [9.0625, 9.2172, 9.3720, 9.5267, 9.6814]]]],
       grad_fn=<ThnnConv2DBackward>)

Changes in image size

import torch.nn as nn
import torch
img=torch.arange(4*64*28*28,dtype=torch.float32).view(4,64,28,28)
conv=nn.Conv2d(in_channels=64,out_channels=128,kernel_size=3,padding=1)
img_2=conv(img)
print(img.shape)
print(img_2.shape)

output

# Before convolution
torch.Size([4, 64, 28, 28])
# After convolution
torch.Size([4, 128, 28, 28])

The number of channels becomes twice that of the original one, and the size remains unchanged after convolution because one grid is filled

Parameters of output convolution operation

Convolution layer value

import torch.nn as nn
import torch
conv=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3)
print(conv.weight)
print(conv.bias)
print(type(conv.weight))
# Call parameters with the. parameters() method
for i in conv.parameters():
    print(i)
print(type(i))

output

# Convolution layer weight parameter
Parameter containing:
tensor([[[[-0.1891, -0.2296,  0.0362],
          [-0.1552, -0.0747,  0.2922],
          [-0.1434,  0.0802, -0.0778]]]], requires_grad=True)
# Convolution layer bias parameters
Parameter containing:
tensor([0.1998], requires_grad=True)
# The types of parameters are Parameter class
<class 'torch.nn.parameter.Parameter'>
# Here are the parameters called through the. parameters() method, which is the same as the previous method result
Parameter containing:
tensor([[[[-0.1891, -0.2296,  0.0362],
          [-0.1552, -0.0747,  0.2922],
          [-0.1434,  0.0802, -0.0778]]]], requires_grad=True)
Parameter containing:
tensor([0.1998], requires_grad=True)
# The data type returned is the same
<class 'torch.nn.parameter.Parameter'>

Convolution layer parameter size

import torch.nn as nn
import torch
conv=nn.Conv2d(in_channels=64,out_channels=128,kernel_size=[5,3],padding=2)
print(conv.weight.shape)
print(conv.bias.shape)

output

# Weight parameters, from the first dimension to the fourth dimension, represent:
# Number of output channels, number of input channels, height of convolution kernel, width of convolution kernel
torch.Size([128, 64, 5, 3])
# The offset term parameter has the same size as the number of input channels
torch.Size([128])

fill style

In order to eliminate the influence of convolution operation on the original graph, we first set the convolution kernel size to 1, and the parameter to 1, without setting the offset term. In order to highlight the expanded effect, we adjust padding to 3.

Initialization process

import torch.nn as nn
import torch
conv_1=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=1,bias=False,padding=3,mode='zeros')
conv_1.weight=nn.parameter(torch.ones((1,1,1,1)))
conv_2=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=1,bias=False,padding=3,mode='reflect')
conv_2.weight=nn.parameter(torch.ones((1,1,1,1)))
conv_3=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=1,bias=False,padding=3,mode='replicate')
conv_3.weight=nn.parameter(torch.ones((1,1,1,1)))
conv_4=nn.Conv2d(in_channels=1,out_channels=1,kernel_size=1,bias=False,padding=3,mode='circular')
conv_4.weight=nn.parameter(torch.ones((1,1,1,1)))
img=torch.arange(25,dtype=torch.float32).reshape(1,1,5,5)

Zero fill

img_1=conv_1(img)
print(img)
print(img_1)

output

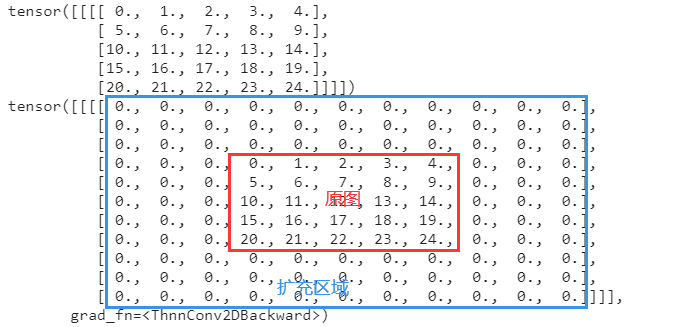
Mirror fill

img_2=conv_2(img)
print(img)
print(img_2)

output

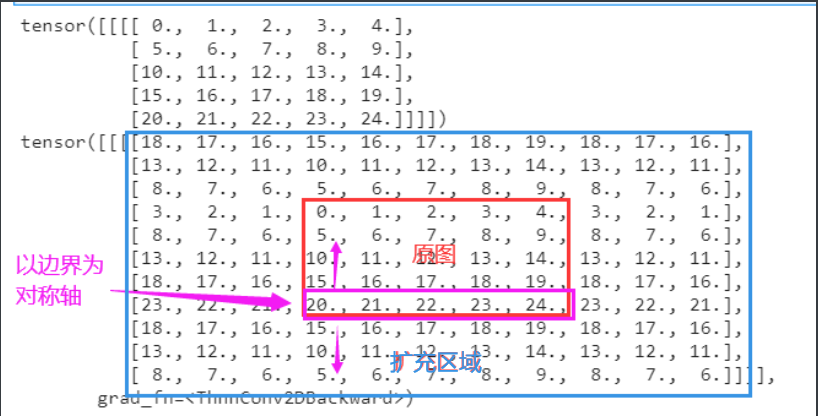
Copy fill

img_3=conv_3(img)
print(img)
print(img_3)

output

Cyclic filling

img_4=conv_4(img)
print(img)
print(img_4)

output

Official documents

nn.Conv2d(): https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html?highlight=conv2d#torch.nn.Conv2d

Point a favor and support it