Transplanting neural network to STM32

A recent project needs to use the network for fitting, and use the fitting results as control. I wonder if I can do neural network calculation directly on the single chip microcomputer, so that I can calculate in real time without relying on the upper computer. Therefore, there are two main problems to be solved, one is the transplantation of neural network, and the other is the computing speed of STM32.

Transplantation of neural network

The network adopts the simplest BP neural network. The basic principle can be understood by yourself, probably through several matrix operations
A X + B AX+B AX+B
Map m inputs to n outputs. Generally, the matrix operation will be followed by an activation function (I don't know if it's called this name). The common ones are sigmoid, tansig and so on. After understanding this, it is transplantation.
Network transplantation can be roughly divided into three steps: training the network, extracting network parameters, and finally writing the predicted code in KEIL. The following is a description combined with examples and codes

Network training

The specific process of training the network is not mentioned. I carry out it in matlab. After training, I can get a network net. Here, the input is 12 variables and the output is 1 variable. The number of neurons in the three-layer network is 50, 50 and 20 respectively.

Network parameter extraction

Network parameter extraction is also carried out in matlab. The code is as follows

load NET3 %network
clear temp
%% Network parameters, but network structure,{}The index inside is different
w{1}=net.IW{1};
w{2}= net.LW{2};
w{3}=net.LW{3,2};
w{4}=net.LW{4,3};
b=net.b;

%%Normalized parameters
[row,col] = find(net.inputConnect==1);   %Get input matrix
ps_Xxmax = net.inputs{row,col}.range(:,2);
ps_Xxmin = net.inputs{row,col}.range(:,1);
ps_Xymax = net.inputs{row,col}.processedRange(:,2);
ps_Xymin = net.inputs{row,col}.processedRange(:,1);
[row,col] = find(net.outputConnect==1);   %Get input matrix
ps_Yxmax = net.outputs{row,col}.range(:,2);
ps_Yxmin = net.outputs{row,col}.range(:,1);
ps_Yymax = net.outputs{row,col}.processedRange(:,2);
ps_Yymin = net.outputs{row,col}.processedRange(:,1);
%% Test input variables
dataX=[19513.4489795918,20577.612244898,20159.6326530612,20345.1020408163,19241.9387755102,19875.1428571429,17836.8163265306,18450.1734693878,19108.2142857143,17741.193877551,20197.5,17988.5
]';
%% Start calculation
temp{1} = (dataX-ps_Xxmin)./(ps_Xxmax-ps_Xxmin).*(ps_Xymax-ps_Xymin)+ ps_Xymin;   %Input normalization
%% Matrix calculation and activation function calculation
for i=2:4
    temp{i} = tansig_apply( w{i-1}*temp{i-1}+b{i-1} );    % front numLayers-1 Cyclic calculation
end
x = w{4}*temp{4}+b{4}         % The last layer is not used tansig function 
dataY = (ps_Yxmax-ps_Yxmin).*(x-ps_Yymin)./(ps_Yymax-ps_Yymin)+ps_Yxmin   %Inverse normalization
%%Finally, the corresponding variables are output to txt，For ease of writing KEIL in
for i=1:length(w)
    d=w{i};
    d=d';
    writematrix(d(:)',['w' num2str(i)]);
end

for i=1:length(b)
    d=b{i};
    writematrix(d(:)',['b' num2str(i)]);
end
 writematrix((ps_Xxmax)','ps_Xxmax');
 writematrix((ps_Xxmin)','ps_Xxmin');
 writematrix((ps_Xymax)','ps_Xymax');
 writematrix((ps_Xymin)','ps_Xymin');

 writematrix((ps_Yxmax)','ps_Yxmax');
  writematrix((ps_Yxmin)','ps_Yxmin');
 writematrix((ps_Yymax)','ps_Yymax');
 writematrix((ps_Yymin)','ps_Yymin');
 
function a = tansig_apply(n,~)      %tansig Function, in order to compile into C
    a = 2 ./ (1 + exp(-2*n)) - 1;
end

The outputs corresponding to the test input variables are as follows

Migrate to KEIL

The next step is to transplant the above matlab code to KEIL. This should not be difficult, because there is no complex algorithm, but we need to use the matrix calculation library
The migration is divided into two steps. The first step is to write the network parameters, and the second step is to realize the calculation process. Because there are too many network parameters, they will not be put here. If you are interested, you can download the source file. Only the code that implements the calculation process is put here.

float32_t Get_Hm(float32_t input[12])
{
	    
		u8 i=0;
//	float32_t tempinput[12];
//	memcpy(tempinput,input,4*12);
	//normalization
	for(i=0;i<12;i++)
	{
		//float32_t t=input[i]-ps_X_xmin[i];
 		input[i]=(input[i]-ps_X_xmin[i])/(ps_X_xmax[i]-ps_X_xmin[i])*(ps_X_ymax[i]-ps_X_ymin[i])+ ps_X_ymin[i];
		//printf("%d: %5f\r\n",i,t);
	}
//		T_C_data[0]=T;
//		T_C_data[1]=C;
//	//temp{1} = (dataX-ps_X.xmin)./(ps_X.xmax-ps_X.xmin).*(ps_X.ymax-ps_X.ymin)+ ps_X.ymin;   // Input normalization
//		T_C_data[0]=(T-ps_X_xmin[0])/(ps_X_xmax[0]-ps_X_xmin[0])*(ps_X_ymax[0]-ps_X_ymin[0])+ ps_X_ymin[0];
//		T_C_data[1]=(C-ps_X_xmin[1])/(ps_X_xmax[1]-ps_X_xmin[1])*(ps_X_ymax[1]-ps_X_ymin[1])+ ps_X_ymin[1];
		//Input hierarchy
	  arm_mat_mult_f32(&W1,&InputM,&h1); 
	
	for(i=0;i<50;i++)
	{
		//printf("%d: %5f\r\n",i,h_data1[i]);
		h_data1[i]=h_data1[i]+B1_data[i];
	}	 
	 for(i=0;i<50;i++)
	 {
		h_data1[i]=2/(1+exp(-2*(h_data1[i])))-1;  //tansig function
	 }
		 //Hidden layer
		 
     arm_mat_mult_f32(&W2,&h1,&h2);
		 for(i=0;i<50;i++)
     {
      h_data2[i]=2/(1+exp(-2*(h_data2[i]+B2_data[i])))-1;  //tansig function
     }
		 arm_mat_mult_f32(&W3,&h2,&h3);
		 for(i=0;i<20;i++)
     {
      h_data3[i]=2/(1+exp(-2*(h_data3[i]+B3_data[i])))-1;  //tansig function
     }
		 arm_mat_mult_f32(&W4,&h3,&OutputM);
		 
//		 Hm_data=2/(1+exp(-2*(Hm_data+B2_data[0])))-1;  //tansig function
//		 //Output layer
		 
     Outputdata=Outputdata+B4_data[0];
		 //Inverse normalization
		 Outputdata = (ps_Y_xmax[0]-ps_Y_xmin[0])*(Outputdata-ps_Y_ymin[0])/(ps_Y_ymax[0]-ps_Y_ymin[0])+ps_Y_xmin[0];   

		 //Hm_data=(Hm_data*(0.9555-0.1055)+0.1055)*100;   
		          
	   return  Outputdata;
}

Result verification

After transplanting, the concern is whether the calculation is right or not and the calculation speed. I always calculate in the loop and send it through the serial port, so I can basically determine the time required for calculation.

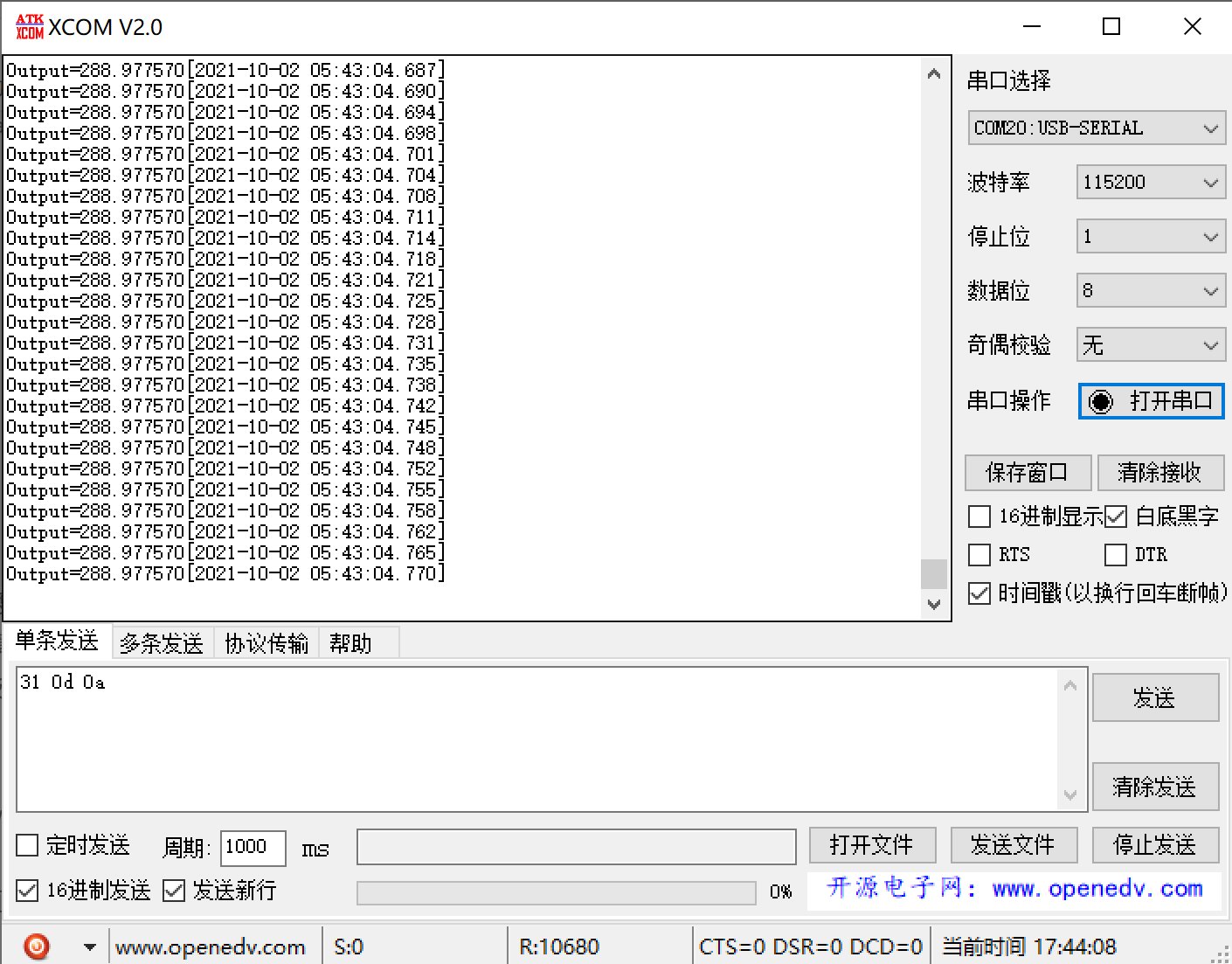
Compared with the matlab calculation results, it can be seen that the calculation speed is basically consistent. Through the time stamp, it can be seen that it is about 0.03-0.05s. In other words, it can basically ensure the frequency of about 20hz, which can be used for my project.

STM32 files can be downloaded through the network disk.
Link: https://pan.baidu.com/s/1vKwwk3UdTDvNR6McFNVmCQ
Extraction code: tysa