• 1,Function grammar
  • 1.1,Syntax overview
  • 1.2,Window detail
    • 1.2.1,ROWS window
    • 1.2.2,RANGE window
• 2,Function usage
  • 2.1,General Statistical Class Function
  • 2.2,Data Sorting Class Function
  • 2.3,Data Distribution Class Function
  • 2.4,Statistical analysis class function
• 3,Supplementary case
• 4,summary

Analytical functions are used to calculate aggregate values of a set of rows. The set of rows defined by analytic function grammar is called a window. The size of the window is determined by the number of physical rows or logical intervals. Sliding windows on each row are defined and determine the range of rows that are computed for a particular row. From the view of query results and query grammar, there are three main differences between analysis function and aggregation function.

• 1. The aggregation function returns only one record per group, while the analysis function returns more than one record per group.
• 2. In a single query, multiple aggregation functions can only act on the same group, while different analysis functions can act on different groups.
• 3. In grouped queries, the query list can only appear fields or constants or expressions that have appeared in aggregation functions or GROUP BY clauses, but the analysis function has no such restrictions.

1. Functional grammar

The analytic function I understand is nothing more than a complex data analysis function consisting of one or more ordinary functions or clauses according to certain rules. In other words, the grammatical rules of some functions or clauses within analytic functions have been described before, and will not be repeated here. This section will focus on the grammar of some functions or clauses that are unique to analytic functions.

1.1. Overview of Grammar

Many websites call analysis function window function, or OVER window function, and some paradoxical concepts are not well understood by me. I consulted it specially. <Oracle Database SQL Reference 10g Release 2>Analytic Functions The grammar is as follows:

analytic_function([arguments]) OVER([analytic_clause])

Description of parameters:

• analytic_function: The name of the analytic function. Oracle 10g R2 has 30 analysis functions built in.
• arguments: Analyse the parameters of the function. Built-in analysis functions usually have 0-3 parameters, which can be any digital type or can be implicitly converted to digital data type.
• OVER: Used to identify a function as an analytic function. For functions that can be used as aggregation function and analysis function, Oracle cannot recognize them. OVER must be used to identify this function as analysis function. But it does not mean that functions that can only be used as analytic functions need not be identified. Analytic functions must be identified by OVER keywords. In addition, a pair of parentheses behind OVER is also necessary, even if nothing is contained in the parentheses.
• analytic_clause: Used to determine analysis rules. The grammar is: [query_partition_clause] [order_by_clause [windows_clause]. All three clauses in the grammar are optional, but windows_clause must depend on order_by_clause.
  • query_partition_clause: Grouping clause for window determination, similar to the GROUP BY syntax.
  • order_by_clause: A sort clause, used to determine window rules, is similar to the syntax of an ORDER BY statement.
  • Windows_clause: The window range clause is used to determine the current calculation range in the grouping.

1.2. Window Details

stay <Oracle Database SQL Reference 10g Release 2> The grammatical schematic diagram of windows_clause is given as follows: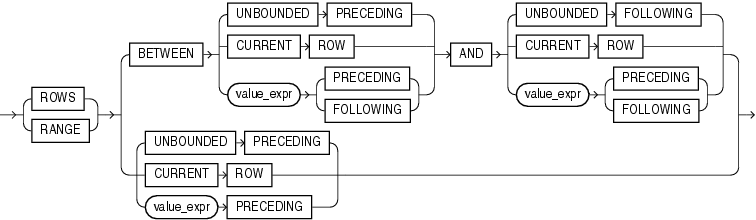

• ROWS: Used to specify that the window consists of physical rows, that is, the range of the specified data rows.
• RANGE: Used to specify a window consisting of a logical offset, that is, a range that meets the specified logical conditions.
• BETWEEN...AND: Used to specify the start and end points of a window.
• UNBOUNDED PRECEDING: Used to indicate that the window begins on the first line of the group.
• CURRENT ROW: As a starting point, specify the value of the window starting at the current row or current row; as a ending point, specify the value of the window ending at the current row or current row.
• UNBOUNDED FOLLOWING: Used to indicate that the window ends on the last line of the group.
• value_expr: An expression of a physical or logical offset.

Whether the window size is determined by the number of physical rows (ROWS) or by the logical interval (RANGE), the window always slides from top to bottom in the grouping. The window range can be limited by BETWEEN...AND, or BETWEEN...AND can not be used to indicate the end of the window to the current line or value.

1.2.1, ROWS window

ROWS window is a window composed of several consecutive rows in a grouping after the grouping is sorted. In the ROWS window, value_expr is a physical offset, which must be a constant or an expression with a non-negative value. There are 16 legal ROWS window scope definitions, listed as follows:

1. The window begins on the first line of the group and ends on the last line of the group.

ROWS BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING

2. The window begins on the first line of the group and ends on the current line.

ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW
ROWS UNBOUNDED PRECEDING

3. The window begins on the first line of the group and ends on the first value_expr line of the current line.

ROWS BETWEEN UNBOUNDED PRECEDING AND value_expr PRECEDING

4. The window begins on the first line of the group and ends on the value_expr line after the current line.

ROWS BETWEEN UNBOUNDED PRECEDING AND value_expr FOLLOWING

5. The window begins on the current line and ends on the last line of the group.

ROWS BETWEEN CURRENT ROW AND UNBOUNDED FOLLOWING

6. The window begins at the current line and ends at the current line.

ROWS BETWEEN CURRENT ROW AND CURRENT ROW
ROWS CURRENT ROW

7. The window begins on the current line and ends on the previous value_expr line of the current line.

ROWS BETWEEN CURRENT ROW AND value_expr PRECEDING

8. The window starts on the current line and ends on the value_expr line after the current line.

ROWS BETWEEN CURRENT ROW AND value_expr FOLLOWING

9. The window begins in the first value_expr line of the current line and ends in the current line.

ROWS BETWEEN value_expr PRECEDING AND CURRENT ROW
ROWS value_expr PRECEDING

10. The window starts on the first value_expr1 line of the current line and ends on the first value_expr2 line of the current line. The premise is to satisfy value_expr1 >= value_expr2.

ROWS BETWEEN value_expr1 PRECEDING AND value_expr2 PRECEDING

11. The window starts on the first value_expr1 line of the current line and ends on the second value_expr2 line of the current line.

ROWS BETWEEN value_expr1 PRECEDING AND value_expr2 FOLLOWING

12. The window starts on the value_expr line after the current line and ends on the last line of the group.

ROWS BETWEEN value_expr FOLLOWING AND UNBOUNDED FOLLOWING

13. The window starts on the post-value_expr1 line of the current line and ends on the post-value_expr2 line of the current line. The premise is to satisfy value_expr1 <= value_expr2.

ROWS BETWEEN value_expr1 FOLLOWING AND value_expr2 FOLLOWING

1.2.2, RANGE window

The RANGE window is a window composed of rows satisfying specified logical conditions in the grouping after grouping sorting. In the RANGE window, value_expr is a logical offset, and it must be a constant or a non-negative expression or interval value. When the value_expr value is a number, the sort field must be a number or date type; when the value_expr value is an interval value, the sort field must be a date type. There are also 16 legitimate definitions of the Range of ANGE windows, as follows:

1. In ascending sort, the expression is between the value of the first line and the value of the last line; in descending sort, the expression is between the value of the last line and the value of the first line.

RANGE BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING

2. In ascending sort, the expression is between the value of the first row and the value of the current row; in descending sort, the expression is between the value of the current row and the value of the first row. If a window is not specified, it defaults to that window.

RANGE BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW
RANGE UNBOUNDED PRECEDING

3. In ascending sort, the expression is between the value of the first row and the value of the current row - value_expr; in descending sort, the expression is between the value of the current row - value_expr and the value of the first row.

RANGE BETWEEN UNBOUNDED PRECEDING AND value_expr PRECEDING

4. In ascending sort, the expression is between the value of the first row and the value of the current row + value_expr; in descending sort, the expression is between the value of the current row + value_expr and the value of the first row.

RANGE BETWEEN UNBOUNDED PRECEDING AND value_expr FOLLOWING

5. In ascending sort, the expression is between the value of the current row and the value of the last row; in descending sort, the expression is between the value of the last row and the value of the current row.

RANGE BETWEEN CURRENT ROW AND UNBOUNDED FOLLOWING

6. The expression is equal to the value of the current row.

RANGE BETWEEN CURRENT ROW AND CURRENT ROW
RANGE CURRENT ROW

7. The expression is between the value of the current row and the value of the current row + value_expr.

RANGE BETWEEN CURRENT ROW AND value_expr FOLLOWING

8. The expression is between the value of the current line - value_expr and the value of the last line.

RANGE BETWEEN value_expr PRECEDING AND UNBOUNDED FOLLOWING

9. The expression is between the value of the current row - value_expr and the value of the current row.

RANGE BETWEEN value_expr PRECEDING AND CURRENT ROW
RANGE value_expr PRECEDING

10. The expression is between the value of the current row - value_expr1 and the value of the current row - value_expr2. The premise is to satisfy value_expr1 >= value_expr2.

RANGE BETWEEN value_expr1 PRECEDING AND value_expr2 PRECEDING

11. The expression is between the value of the current row - value_expr1 and the value of the current row + value_expr2.

RANGE BETWEEN value_expr1 PRECEDING AND value_expr2 FOLLOWING

12. In ascending sort, the expression is between the value of the current row + value_expr and the value of the last row; in descending sort, the expression is between the value of the last row and the value of the current row + value_expr.

RANGE BETWEEN value_expr FOLLOWING AND UNBOUNDED FOLLOWING

13. The expression is between the value of the current row + value_expr1 and the value of the current row + value_expr2. The premise is to satisfy value_expr1 <= value_expr2.

RANGE BETWEEN value_expr1 FOLLOWING AND value_expr2 FOLLOWING

2. Functional Usage

There are 38 built-in analytical functions in Oracle 10g R2. In this section, they are classified into four categories according to their functions: general statistical functions, data sorting functions, data distribution functions and statistical analysis functions. The definitions and usage examples of functions are given one by one.

2.1. General statistical class functions

• MAX: Maximize the field or expression in the data window within a group.
• MIN: Minimize fields or expressions in data windows within a group.
• AVG: Average the field or expression in the data window within a group.
• SUM: Total values of fields or expressions in a data window within a group.
• COUNT: Cumulative count of rows in data windows within a group.

Example 1:

SELECT t.staff_name,t.dept_code,t.base_salary,t.post_salary,
  MAX(t.post_salary) OVER(PARTITION BY t.dept_code) max_salary,  -- Department's highest post salary
  MIN(t.post_salary) OVER(PARTITION BY t.dept_code) min_salary,  -- Minimum Wage for Departments
  AVG(t.post_salary) OVER(PARTITION BY t.dept_code) avg_salary,  -- Average post salary of Department
  SUM(t.post_salary) OVER(PARTITION BY t.dept_code) sum_salary,  -- The sum of department post wages
  COUNT(t.post_salary) OVER(PARTITION BY t.dept_code) cnt_salary -- Departmental Wages
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

Example 2:

SELECT t.staff_name,t.dept_code,t.base_salary,t.post_salary,
  -- Maximum post wages up to the present level in the Department
  MAX(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary ROWS UNBOUNDED PRECEDING) max_salary,
  -- Minimum Post Wage in the Current to Last Line of Departments
  MIN(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary ROWS CURRENT ROW) min_salary,
  -- Average post salary in the first line to the previous line of the Department
  AVG(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary ROWS BETWEEN UNBOUNDED PRECEDING AND 1 PRECEDING) avg_salary,
  -- The sum of the salaries of the first and the second lines in the Department
  SUM(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary ROWS BETWEEN UNBOUNDED PRECEDING AND 1 FOLLOWING) sum_salary,
  -- Number of salaries in the Department up to the present line
  COUNT(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary ROWS UNBOUNDED PRECEDING) cnt_salary
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

2.2. Data Sorting Class Function

• RANK(): According to ORDER BY's ranking results, the relative positions between groups are calculated, and the hopping sign is possible. The data in the group is sorted by the ORDER BY clause, and each row will get a serial number, thus forming a sequence. The sequence starts from 1, and every time the value of the ORDER BY expression changes, the sequence will be added to 1. Lines with the same value will get the same ordinal number (NULL is considered equal), and the ordinal number of subsequent lines will jump. If the serial number of the first two lines is 1, there is no serial number 2, and the third line will get the serial number 3.
• DENSE_RANK(): According to ORDER BY's ranking results, the relative positions between groups are calculated, and no sign hopping is performed. DENSE_RANK is similar to RANK in that it also obtains an isometric sequence with the first item being 1 and the tolerance being 1, and the same line number with the same value (NULL is also considered equal), but the serial number will not jump. If the first two lines are numbered 1, the third line will be numbered 2.
• FIRST_VALUE(expression): Returns the first value of the data window in the group.
• LAST_VALUE(expression): Returns the last value of the data window in the group.
• LAG(expression [, offset [, default]]): You can access rows before the current row in the result set without having to self-connect, so that rows before the current row can be selected from the group together with the current row. Offset is a positive integer with a default value of 1. If offset is not specified or the offset value exceeds the window range, the default value is enabled.
• LEAD(expression [, offset [, default]]): In contrast to LAG, LEAD can access rows after the current row in the result set without self-joining, so that rows after the current row can be selected from the group together with the current row. Offset is a positive integer with a default value of 1. If offset is not specified or the offset value exceeds the window range, the default value is enabled.
• ROW_NUMBER: Returns the offset of a row in an ordered group and assigns the line number in a specific order.
• FIRST: Screen out the rows with the first value from the compact sorted result set (probably multiple rows, because the values may be equal).
• LAST: Screen out the rows with the last value from the compact sorted result set (probably multiple rows, because the values may be equal).

Example 1:

SELECT t.dept_code,t.staff_name,t.post_salary,
  RANK() OVER(ORDER BY t.dept_code,t.post_salary) rank,
  DENSE_RANK() OVER(ORDER BY t.dept_code,t.post_salary) dense_rank,
  FIRST_VALUE(t.post_salary) OVER(ORDER BY t.dept_code,t.post_salary) fist_value,
  LAST_VALUE(t.post_salary) OVER(ORDER BY t.dept_code,t.post_salary) last_value,
  LAG(t.post_salary,1,0) OVER(ORDER BY t.dept_code,t.post_salary) lag_value,
  LEAD(t.post_salary,1,0) OVER(ORDER BY t.dept_code,t.post_salary) lead_value,
  ROW_NUMBER() OVER(ORDER BY t.dept_code,t.post_salary) row_number
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

Example 2:

SELECT t.dept_code,t.staff_name,t.birthday,t.post_salary,
  RANK() OVER(PARTITION BY t.dept_code ORDER BY t.post_salary) rank,
  DENSE_RANK() OVER(PARTITION BY t.dept_code ORDER BY t.post_salary) dense_rank,
  FIRST_VALUE(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary) fist_value,
  LAST_VALUE(t.post_salary) OVER(PARTITION BY t.dept_code ORDER BY t.post_salary) last_value,
  LAG(t.post_salary,1,0) OVER(PARTITION BY t.dept_code ORDER BY t.dept_code,t.post_salary) lag_value,
  LEAD(t.post_salary,1,0) OVER(PARTITION BY t.dept_code ORDER BY t.dept_code,t.post_salary) lead_value,
  ROW_NUMBER() OVER(PARTITION BY t.dept_code ORDER BY t.dept_code,t.post_salary) row_number
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

Example 3:

SELECT t.staff_name,t.gender,t.dept_code,t.post_salary,
  MIN(t.post_salary) KEEP(DENSE_RANK FIRST ORDER BY t.dept_code) OVER(PARTITION BY t.gender) first_value1,
  MAX(t.post_salary) KEEP(DENSE_RANK FIRST ORDER BY t.dept_code) OVER(PARTITION BY t.gender) first_value2,
  MIN(t.post_salary) KEEP(DENSE_RANK LAST ORDER BY t.dept_code) OVER(PARTITION BY t.gender) last_value1,
  MAX(t.post_salary) KEEP(DENSE_RANK LAST ORDER BY t.dept_code) OVER(PARTITION BY t.gender) last_value2
FROM demo.t_staff t 
ORDER BY t.gender,t.dept_code;

2.3. Data Distribution Class Function

• RATIO_TO_REPORT(expr): Calculates the ratio of the value of the current row to the sum of the values of all rows in the group.
• NTILE(expr): An ordered set of data is divided into several buckets and the corresponding bucket number is assigned to each row. Expr must be a value or expression that can be resolved into positive integers, and if decimal, the decimal part will be intercepted. The barrel number ranges from 1 to TRUNC(expr), with a maximum difference of 1 rows per barrel. If rows are not divisible by barrels, the barrel in front will be filled first, and the barrel in back will have one less row of data. For example, expr=3, row number = 16, the barrel number is 1 with 6 lines, and the barrel number is 2 or 3 with 5 lines.
• CUME_DIST(): Calculates the cumulative distribution of a set of values and returns a number greater than 0, less than or equal to 1, which represents the relative position of the row in the group, and adjacent rows with equal values will get the same cumulative distribution value.
• PERCENT_RANK(): Similar to the CUME_DIST function, the value of each line is equal to the line number of that line minus 1 first, then divided by the total number of rows in the group minus 1, so the return value is always greater than or equal to 0, less than or equal to 1.
• PERCENTILE_DISC(expr): Returns a value that corresponds to the distribution percentage. For the calculation of the distribution percentage, see the CUME_DIST function (NULL is ignored when calculating).
• PERCENTILE_CONT(expr): Returns a value that corresponds to the distribution percentage. The calculation method of the distribution percentage refers to the PERCENT_RANK function (NULL is ignored when calculating).
• REGR (Linear Regression) Functions: These linear regression functions are suitable for the least squares regression line. There are nine different regression functions.
  • REGR_SLOPE: Return slope. Equivalent to COVAR_POP(expr1, expr2) / VAR_POP(expr2).
  • REGR_INTERCEPT: y intercept to return the regression line. Equivalent to AVG(expr1) - REGR_SLOPE(expr1, expr2) * AVG(expr2).
  • REGR_COUNT: Returns the number of non-empty number pairs used to fill the regression line.
  • REGR_R2: The determinant of returning to the regression line. If VAR_POP(expr2) = 0, it is NULL; if VAR_POP(expr1) = 0 and VAR_POP (expr2)!= 0, it is 1; if VAR_POP (expr1) > 0 and VAR_POP (expr2)!= 0, it is POWER(CORR(expr1,expr),2).
  • REGR_AVGX: Calculate the average of the regression line independent variable (expr2). After removing the empty pair (expr1,expr2), it is equivalent to AVG(expr2).
  • REGR_AVGY: Calculate the average of regression line strain (expr1). After removing the empty pair (expr1,expr2), it is equivalent to AVG(expr1).
  • REGR_SXX: After removing empty pairs (expr1,expr2), it is equivalent to REGR_COUNT (expr1,expr2)* VAR_POP (expr2).
  • REGR_SYY: After removing empty pairs (expr1,expr2), it is equivalent to REGR_COUNT (expr1,expr2)* VAR_POP (expr1).
  • REGR_SXY: After removing empty pairs (expr1,expr2), it is equivalent to REGR_COUNT (expr1,expr2)* COVAR_POP (expr1,expr2).

Example 1:

SELECT t.staff_name,t.dept_code,t.post_salary,
  RATIO_TO_REPORT(t.post_salary) OVER() ratio_to_report,
  NTILE(3) OVER(ORDER BY t.dept_code,t.post_salary) ntile,
  CUME_DIST() OVER(ORDER BY t.dept_code,t.post_salary) cume_dist,
  PERCENT_RANK() OVER(ORDER BY t.dept_code,t.post_salary) percent_rank
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

Example 2:

SELECT t.staff_name,t.dept_code,t.post_salary,
  RATIO_TO_REPORT(t.post_salary) OVER(PARTITION BY t.dept_code) ratio_to_report,
  NTILE(3) OVER(PARTITION BY t.dept_code ORDER BY t.dept_code,t.post_salary) ntile,
  CUME_DIST() OVER(PARTITION BY t.dept_code ORDER BY t.dept_code,t.post_salary) cume_dist,
  PERCENT_RANK() OVER(ORDER BY t.dept_code,t.post_salary) percent_rank,
  PERCENTILE_DISC(0.5) WITHIN GROUP(ORDER BY t.post_salary) OVER(PARTITION BY t.dept_code) percentile_disc,
  PERCENTILE_CONT(0.5) WITHIN GROUP(ORDER BY t.post_salary) OVER(PARTITION BY t.dept_code) percentile_cont
FROM demo.t_staff t 
ORDER BY t.dept_code,t.post_salary;

2.4. Statistical analysis class function

• CORR(expr1, expr2): Returns a logarithmic correlation coefficient. Equivalent to COVAR_POP (expr1, expr2)/ (STDDEV_POP (expr1)* STDDEV_POP (expr2).
• COVAR_POP(expr1, expr2): Returns a pair of logarithmic population covariances. Equivalent to (SUM(expr1 * expr2) - SUM(expr2) * SUM(expr1) / n) / n.
• COVAR_SAMP(expr1, expr2): Returns a pair of sample covariances. Equivalent to (SUM(expr1 * expr2) - SUM(expr1) * SUM(expr2) / n) / (n-1).
• STDDEV([DISTINCT | ALL] expr): Calculates the standard deviation of the current row with respect to the group.
• STDDEV_POP(expr): Calculates the total standard deviation and returns the square root of the total variance. The square root of the VAR_POP function is the same.
• STDDEV_SAMP(expr): Calculates the cumulative sample standard deviation and returns the square root of the sample variance. The square root of the VAR_SAMP function is the same.
• VAR_POP(expr): Returns the total variance of non-null (i.e. ignoring NULL) pairs.
• VAR_SAMP(expr): Returns the sample variance of non-null (i.e. ignoring NULL) pairs.
• VARIANCE ([DISTINCT | ALL] expr): If expr = 1, return 0; if expr > 1, return VAR_SAMP.

3. Supplementary cases

Case 1, progressive accumulation (the case is very useful in realizing functions such as write-offs and deductions):

WITH t AS(
  SELECT 1 val FROM DUAL UNION ALL
  SELECT 3 FROM DUAL UNION ALL
  SELECT 5 FROM DUAL UNION ALL
  SELECT 7 FROM DUAL UNION ALL
  SELECT 9 FROM DUAL
)
SELECT t.val,
  SUM(t.val) OVER(ORDER BY ROWNUM ROWS UNBOUNDED PRECEDING) cur_sum_val,
  SUM(t.val) OVER(ORDER BY ROWNUM ROWS BETWEEN UNBOUNDED PRECEDING AND 1 PRECEDING) pre_sum_val 
FROM t;

Result:

       VAL CUR_SUM_VAL PRE_SUM_VAL
---------- ----------- -----------
         1           1 
         3           4           1
         5           9           4
         7          16           9
         9          25          16

Case 2: Take the row with the smallest value in A and B levels (the case is very useful in the statistical analysis of the progress plan at the present stage):

WITH t AS(
  SELECT 'A' grade, 1 val FROM DUAL UNION ALL
  SELECT 'A',3 FROM DUAL UNION ALL
  SELECT 'A',5 FROM DUAL UNION ALL
  SELECT 'B',7 FROM DUAL UNION ALL
  SELECT 'B',9 FROM DUAL
)
SELECT t2.grade,t2.val FROM(
  SELECT t.grade,t.val,RANK() OVER(PARTITION BY t.grade ORDER BY val) rank FROM t
) t2 WHERE t2.rank=1;

Result:

GRADE        VAL
----- ----------
A              1
B              7

Case 3 identifies the oldest and youngest employees in each department:

SELECT DISTINCT t1.dept_code,t2.enum_name dept_name,
  FIRST_VALUE(t1.staff_name) OVER(PARTITION BY t1.dept_code ORDER BY t1.birthday) max_older_name,
  FIRST_VALUE(t1.staff_name) OVER(PARTITION BY t1.dept_code ORDER BY t1.birthday DESC) min_young_name
FROM demo.t_staff t1
LEFT JOIN demo.t_field_enum t2 ON t2.field_code='DEPT' AND t1.dept_code=t2.enum_code
ORDER BY t1.dept_code; -- Note: Once used here DISTINCT，ORDER BY The fields in the list must be SELECT Listed

Result:

DEPT_CODE                DEPT_NAME                    MAX_OLDER_NAME               MIN_YOUNG_NAME
------------------------ ---------------------------- ---------------------------- ---------------------------
010101                   Research and Development Department                     Xiao Ming                         WangTwo
010102                   R & D two                     Little SA                         Kobayashi
010103                   R & D three                     Han three                         Xiaoling
010104                   Test department                       Xiaomei                         Xiaoyan
010201                   Implement one                     Small army                         Xiaohong
010202                   Implementation of the two Department                     Xiaofei                         Xiaofei

summary

Strictly speaking, this article should be regarded as an introduction to analytic functions, because it only describes the grammar and simple usage of analytic functions. Although there are many window rules, as long as we do a little analysis, we will find that it is not really complicated. The key point is to be able to use flexibly according to the actual situation. The best reference is Supplementary Case 1. I started my analysis function journey after I saw an SQL statement similar to that in Supplementary Case 1 on the Internet myself! __________ Coincidentally, it didn't take long for the company's financial requirements to add smart write-off function to the reimbursement process, just to use it!

This article lists all the analysis functions in Oracle 10g. Among them, I have used some general statistical and data sorting functions, because in addition to explaining the use of functions, I have also given some examples. But most of the data distribution function and statistical analysis function only give simple explanations, mainly because they are seldom used in daily development, and most of them I have never used. For further information, please refer to the official manual: Analytic Functions.