Doorman
Topic overview



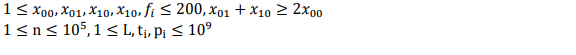
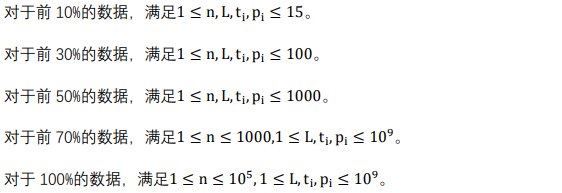
Problem solution
Sister's favorite tree set tree optimization dp.
First, it should be easy to come up with a
d
p
dp
The idea of dp.
As Niuniu has only two movements in the whole process, stay at the door, run back to rest and run back.
We can define
d
p
i
,
0
/
1
dp_{i,0/1}
dpi,0/1 , indicates whether Niu Niu is staying at the door or resting again. However, in this case, it is very troublesome to deal with the reception of guests, and it may be stressful. We might as well just look at him when he stays at the door to receive guests.
definition
d
p
i
dp_{i}
dpi , means he's in time
i
i
There are two kinds of shifts in the total contribution of staying at the door at i, one is staying at the door at the last moment, and the other is running back to rest from a previous moment and running back now.
In the first case, the guests can be received as soon as they arrive, and the total value of the guests can be directly added.
The second is equivalent to that you will not receive the guests in this section when they come. You will only receive them when you come, which is the contribution of the middle period of time.
We also found that such a transfer, the second transfer also has interval restrictions, and you can't miss a guest completely.
But we found that if, as we said above
d
p
dp
dp, we find that the only effective time nodes are the arrival time of someone and the departure time of someone.
Because of our
d
p
dp
In fact, the contribution of dp transfer is in the form of straight line with fixed slope, so our optimal decision point is willing to be on a certain time node.
We can just take the time node as a reference
d
p
dp
dp status, definition page
i
i
i time nodes are
b
i
b_{i}
bi.
Obviously, it can be obtained
d
p
dp
dp transfer type,
d
p
i
=
max
(
d
p
i
−
1
−
(
b
i
−
b
i
−
1
)
x
0
,
0
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
p
k
,
max
j
=
L
i
R
i
(
d
p
j
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
(
b
i
−
b
j
−
2
L
)
x
1
,
1
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
(
t
k
+
p
k
−
b
i
)
)
)
dp_{i}=\max\left(dp_{i-1}-(b_{i}-b_{i-1})x_{0,0}+\sum_{t_{k}\in(b_{i-1},b_{i}]}f_{k}p_{k},\max_{j=L_{i}}^{R_{i}}\left(dp_{j}-L(x_{1,0}+x_{0,1}+2x_{1,1})+(b_{i}-b_{j}-2L)x_{1,1}+\sum_{t_k\in(b_{i-1},b_{i}]}f_k(t_k+p_k-b_i)\right)\right)
dpi=max⎝⎛dpi−1−(bi−bi−1)x0,0+tk∈(bi−1,bi]∑fkpk,j=LimaxRi⎝⎛dpj−L(x1,0+x0,1+2x1,1)+(bi−bj−2L)x1,1+tk∈(bi−1,bi]∑fk(tk+pk−bi)⎠⎞⎠⎞
about
L
i
L_{i}
Li and
R
i
R_{i}
Ri, these two are obviously not healthy. We should be able to easily
O
(
n
)
O\left(n\right)
O(n) is processed.
And for the above
d
p
dp
dp formula, we can change it again,
d
p
i
=
max
(
d
p
i
−
1
−
(
b
i
−
b
i
−
1
)
x
0
,
0
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
p
k
,
b
i
x
1
,
1
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
max
j
=
L
i
R
i
(
d
p
j
−
b
j
x
1
,
1
+
∑
t
k
∈
(
b
i
−
1
,
b
i
]
f
k
(
t
k
+
p
k
−
b
i
)
)
)
dp_{i}=\max\left(dp_{i-1}-(b_{i}-b_{i-1})x_{0,0}+\sum_{t_{k}\in(b_{i-1},b_{i}]}f_{k}p_{k},b_{i}x_{1,1}-L(x_{1,0}+x_{0,1}+2x_{1,1})+\max_{j=L_{i}}^{R_{i}}\left(dp_{j}-b_{j}x_{1,1}+\sum_{t_{k}\in(b_{i-1},b_{i}]}f_{k}(t_{k}+p_{k}-b_{i})\right)\right)
dpi=max⎝⎛dpi−1−(bi−bi−1)x0,0+tk∈(bi−1,bi]∑fkpk,bix1,1−L(x1,0+x0,1+2x1,1)+j=LimaxRi⎝⎛dpj−bjx1,1+tk∈(bi−1,bi]∑fk(tk+pk−bi)⎠⎞⎠⎞
In this case, the slope optimization is obvious. Let's take another look and simplify it,
definition
s
u
m
i
=
∑
t
k
⩽
b
i
f
k
(
t
k
+
p
k
)
sum_{i}=\sum_{t_{k}\leqslant b_{i}}f_{k}(t_{k}+p_{k})
sumi=∑tk⩽bifk(tk+pk),
s
u
m
p
i
=
∑
t
k
⩽
b
i
f
k
p
k
sump_{i}=\sum_{t_{k}\leqslant b_{i}}f_{k}p_{k}
sumpi=∑tk⩽bifkpk,
s
u
m
f
i
=
∑
t
k
⩽
b
i
f
k
sumf_{i}=\sum_{t_{k}\leqslant b_{i}}f_{k}
sumfi=∑tk⩽bifk
So there
d
p
i
=
max
(
d
p
i
−
1
−
(
b
i
−
b
i
−
1
)
x
0
,
0
+
s
u
m
p
i
−
s
u
m
p
i
−
1
,
b
i
x
1
,
1
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
max
j
=
L
i
R
i
(
d
p
j
+
s
u
m
i
−
s
u
m
j
−
b
j
x
1
,
1
+
(
s
u
m
f
i
−
s
u
m
f
j
)
b
i
)
)
dp_{i}=\max\left(dp_{i-1}-(b_{i}-b_{i-1})x_{0,0}+sump_{i}-sump_{i-1},b_{i}x_{1,1}-L(x_{1,0}+x_{0,1}+2x_{1,1})+\max_{j=L_{i}}^{R_{i}}\left(dp_{j}+sum_{i}-sum_{j}-b_{j}x_{1,1}+(sumf_{i}-sumf_{j})b_{i}\right)\right)
dpi=max(dpi−1−(bi−bi−1)x0,0+sumpi−sumpi−1,bix1,1−L(x1,0+x0,1+2x1,1)+j=LimaxRi(dpj+sumi−sumj−bjx1,1+(sumfi−sumfj)bi))
Previously defined
c
o
s
t
i
=
(
b
i
−
b
i
−
1
)
x
0
,
0
+
s
u
m
p
i
−
s
u
m
p
i
−
1
cost_{i}=(b_{i}-b_{i-1})x_{0,0}+sump_{i}-sump_{i-1}
costi = (bi − bi − 1) x0,0 + sumpi − sumpi − 1, and then
i
i
i related or related
j
j
j about division, and
j
j
j irrelevant.
definition
A
i
=
b
i
x
1
,
1
−
L
(
x
1
,
0
+
x
0
,
1
+
2
x
1
,
1
)
+
s
u
m
i
+
s
u
m
f
i
b
i
A_{i}=b_{i}x_{1,1}-L(x_{1,0}+x_{0,1}+2x_{1,1})+sum_{i}+sumf_{i}b_{i}
Ai=bix1,1−L(x1,0+x0,1+2x1,1)+sumi+sumfibi,
B
j
=
d
p
j
−
s
u
m
j
−
b
j
x
1
,
1
B_{j}=dp_{j}-sum_{j}-b_{j}x_{1,1}
Bj=dpj−sumj−bjx1,1,
C
j
=
s
u
m
f
j
C_{j}=sumf_{j}
Cj=sumfj,
D
i
=
b
i
D_{i}=b_{i}
Di=bi,
Then the original formula becomes:
d
p
i
=
max
(
d
p
i
−
1
+
c
o
s
t
i
,
A
i
+
max
j
=
L
i
R
i
(
B
j
+
C
j
D
i
)
)
dp_{i}=\max\left(dp_{i-1}+cost_{i},A_{i}+\max_{j=L_{i}}^{R_{i}}(B_{j}+C_{j}D_{i})\right)
dpi=max(dpi−1+costi,Ai+j=LimaxRi(Bj+CjDi))
Very obvious slope optimization formula, for each
d
p
i
dp_{i}
dpi, all have fixed
x
=
D
i
x=D_{i}
x=Di and
A
i
A_{i}
Ai, go ahead
[
L
i
,
R
i
]
[L_{i},R_{i}]
Find a straight line in [Li, Ri]
y
=
B
j
+
C
j
x
y=B_{j}+C_{j}x
y=Bj + Cj ^ x find the largest to transfer.
Since it is the transfer of a straight line, it is easy to think of maintaining it through the Li Chao line segment tree.
But even if
L
i
,
R
i
L_{i},R_{i}
Li and Ri , are incremental. Li Chao's line segment tree is not easy to maintain. I can't call the priority queue.
But we can set trees. The outer line segment tree maintains the interval, and the inner Li Chao line segment tree maintains our line segments. That's OK.
Tree nest tree optimization
d
p
dp
dp is a traditional art after all.
In fact, it can also be maintained in blocks. In this way, the space may be smaller, but the time complexity will be larger.
But it doesn't matter. Small constants run fast.
Just run like this
d
p
dp
dp is OK.
Time complexity
O
(
n
log
2
n
)
O\left(n\log^2n\right)
O (nlog2n) (nested tree) or
O
(
n
n
log
n
)
O\left(n\sqrt{n\log\,n}\right)
O(nnlogn
) (block).
Priority queues seem to work
O
(
n
log
n
)
O\left(n\log\,n\right)
O(nlogn).
As for the standard range
O
(
n
log
2
n
)
O\left(n\log^2n\right)
O(nlog2n) I don't understand what Li Chaoshu did.
Source code
#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=1e9+7;
const int inv2=499122177;
const int jzm=2333;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<LL,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
struct ming{int f,t,p;}s[MAXN];
struct line{
LL k,b;line(){k=0;b=-1e15;}
line(LL K,LL B){k=K;b=B;}
LL ask(const int x){return 1ll*x*k+b;}
};
int n,L,x00,x01,x10,x11,b[MAXN],tott,dL[MAXN],dR[MAXN],d[MAXN];
LL dp[MAXN],sumf[MAXN],summ[MAXN],ans,sump[MAXN];
struct tann{line s;int lson,rson;};
class SegmentTree{
private:
tann tr[MAXN*100];int tot,root[MAXN<<2];
void insert(int &rt,int l,int r,line aw){
if(l>r)return ;if(!rt)rt=++tot;int mid=l+r>>1;
if(tr[rt].s.ask(b[mid])<aw.ask(b[mid]))swap(tr[rt].s,aw);
if(l<mid&&tr[rt].s.ask(b[l])<aw.ask(b[l]))insert(tr[rt].lson,l,mid-1,aw);
if(r>mid&&tr[rt].s.ask(b[r])<aw.ask(b[r]))insert(tr[rt].rson,mid+1,r,aw);
}
LL query(int rt,int l,int r,int ai){
if(l>ai||r<ai||!rt)return -INF;
int mid=l+r>>1;LL res=tr[rt].s.ask(b[ai]);
if(ai<mid)res=max(res,query(tr[rt].lson,l,mid-1,ai));
if(ai>mid)res=max(res,query(tr[rt].rson,mid+1,r,ai));
return res;
}
public:
#define lson (rt<<1)
#define rson (rt<<1|1)
void Insert(int rt,int l,int r,int ai,line aw){
if(l>ai||r<ai)return ;int mid=l+r>>1;
insert(root[rt],0,tott,aw);if(l==r)return ;
if(ai<=mid)Insert(lson,l,mid,ai,aw);
else Insert(rson,mid+1,r,ai,aw);
}
LL Query(int rt,int l,int r,int al,int ar,int ai){
if(l>r||l>ar||r<al||al>ar)return -INF;
if(al<=l&&r<=ar)return query(root[rt],0,tott,ai);
int mid=l+r>>1;LL res=-INF;
if(al<=mid)res=max(res,Query(lson,l,mid,al,ar,ai));
if(ar>mid)res=max(res,Query(rson,mid+1,r,al,ar,ai));
return res;
}
#undef lson
#undef rson
}T;
signed main(){
freopen("D.in","r",stdin);
freopen("D.out","w",stdout);
read(n);read(L);int maxx=0;
read(x00);read(x01);read(x10);read(x11);
for(int i=1;i<=n;i++)
read(s[i].t),read(s[i].p),read(s[i].f),
b[++tott]=s[i].t,b[++tott]=s[i].t+s[i].p;
sort(b+1,b+tott+1);tott=unique(b+1,b+tott+1)-b-1;
for(int i=1;i<=n;i++){
int tmp=lower_bound(b+1,b+tott+1,s[i].t)-b;
summ[tmp]+=1ll*s[i].f*(s[i].t+s[i].p);
sumf[tmp]+=1ll*s[i].f;maxx=max(maxx,tmp);
sump[tmp]+=1ll*s[i].f*s[i].p;
int tp=upper_bound(b+1,b+tott+1,s[i].t+s[i].p)-b;d[tp]=max(d[tp],tmp);
}
for(int i=1;i<=tott;i++)summ[i]+=summ[i-1],sumf[i]+=sumf[i-1],sump[i]+=sump[i-1];
for(int i=1;i<=tott;i++)dR[i]=min(i-1,maxx-1);
for(int i=1;i<=tott;i++)dL[i]=max(dL[i-1],d[i]);
dp[0]=0;T.Insert(1,0,tott,0,line(0LL,0LL));
for(int i=1;i<=tott;i++){
dp[i]=dp[i-1]-1ll*(b[i]-b[i-1])*x00+sump[i]-sump[i-1];
LL tmpa=1ll*b[i]*x11-1ll*L*(x01+x10+x11+x11)+summ[i]-1ll*b[i]*sumf[i];
LL tmpb=T.Query(1,0,tott,dL[i],dR[i],i);dp[i]=max(dp[i],tmpb+tmpa);
T.Insert(1,0,tott,i,line(sumf[i],dp[i]-1ll*b[i]*x11-summ[i]));
if(i>=maxx)ans=max(ans,dp[i]);
}
printf("%lld\n",ans);
return 0;
}