Title Description
Congcong and Coco brothers often fight over trivial matters, such as the last ice stick left at home and both want to eat, and both want to play with computers (but they only have one computer)... When faced with this problem, stone scissors are usually good, but they are tired of playing such low IQ games.
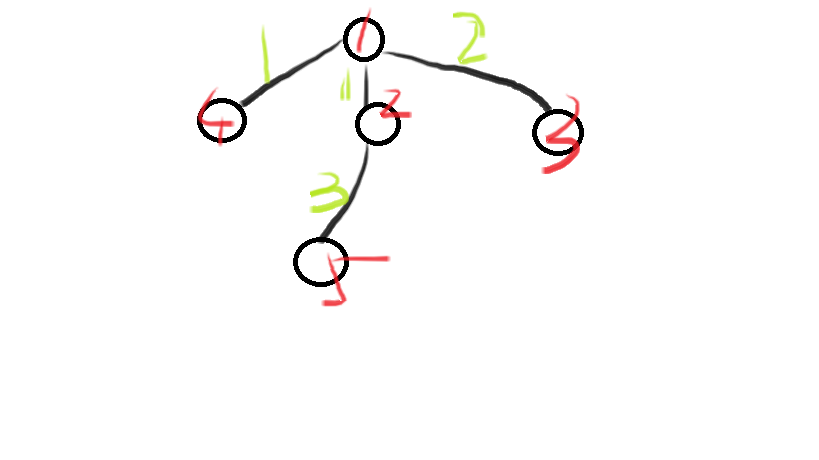
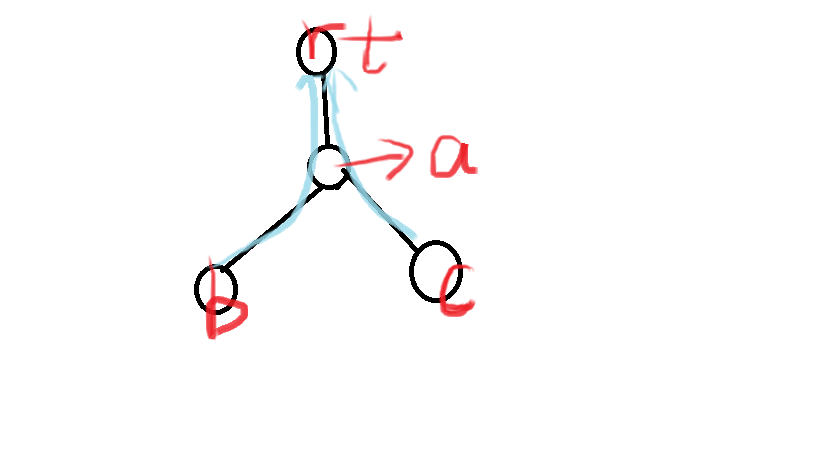
Their father was tired of their quarrel, so he invented a new game: his father drew n "points" on paper and connected them with n-1 "edges" (in fact, this is a tree). And there is a number on each edge. Next, Congcong and Cocoa choose one point (of course, they can't see the tree when choosing the point). If the sum of all the edges between the two points is exactly a multiple of three, Congcong wins, otherwise it can win.
Congcong is very fond of thinking. After every game, he will study the tree carefully, hoping to know what his winning probability is for this picture. Now, please help me to find out the value to verify whether Congcong's answer is correct.
Input format
The first line of input contains a positive integer n. The next n-1 line, each line with three integers x, y, w, indicates that there is an edge between the point X and the point y, and the number above is w.
Output format
Output this probability in the form of approximate fractions (i.e. in the form of "a/b", where a and B must be mutually prime. If the probability is 1, output "1/1".
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
const int maxn=20005;
using namespace std;
template<typename T>inline void rd(T&x)
{
char c;bool f=0;
while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
x=c^48;
while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
if(f)x=-x;
}
int n,m,rt,k,SIZE,hd[maxn],ANS;
int f[maxn],dis[maxn],use[maxn],cnt[10],size[maxn];
struct node
{
int to,nt,val;
}e[maxn<<1];
inline void add(int x,int y,int z)
{
e[++k].to=y;e[k].nt=hd[x];hd[x]=k;e[k].val=z;
e[++k].to=x;e[k].nt=hd[y];hd[y]=k;e[k].val=z;
}
inline void Get_rt(int x,int fa)
{
size[x]=1;f[x]=0;
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v]||v==fa)continue;
Get_rt(v,x);
f[x]=max(f[x],size[v]);
size[x]+=size[v];
}
f[x]=max(f[x],SIZE-size[x]);
if(f[rt]>f[x])rt=x;
}
inline void Get_dis(int x,int fa)
{
++cnt[dis[x]];
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v]||v==fa)continue;
dis[v]=(dis[x]+e[i].val)%3;
Get_dis(v,x);
}
}
inline int Get_num(int x,int D)
{
cnt[1]=cnt[2]=cnt[0]=0;
dis[x]=D%3;
Get_dis(x,0);
re cnt[0]*cnt[0]+cnt[1]*cnt[2]+cnt[2]*cnt[1];
}
inline void dfs(int x)
{
use[x]=1;ANS+=Get_num(x,0);
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v])continue;
ANS-=Get_num(v,e[i].val);
//Excuse me, subtract all invalid states
f[rt=0]=n;SIZE=size[v];
Get_rt(v,0);
dfs(rt);
}
}
inline int gcd(int a,int b){re b?gcd(b,a%b):a;}
int main()
{
freopen("in.txt","r",stdin);
rd(n);
int x,y,z;
inc(i,2,n)
{
rd(x),rd(y),rd(z);
add(x,y,z);
}
f[rt]=SIZE=n;
Get_rt(1,0);
dfs(rt);
int d=gcd(ANS,n*n);
printf("%d/%d",ANS/d,n*n/d);
re 0;
}