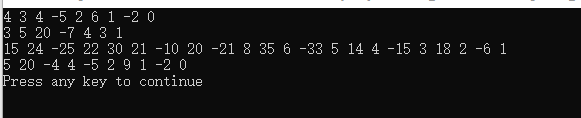
Interpretation of Subject Meaning

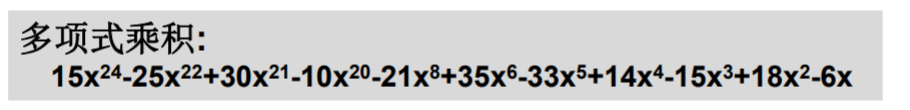

Solution Thought
1. Polynomial Representation
Data Structure Design
//Separating struct from typedef
typedef struct PolyNode *Polynomial; //Use typedef to create a new alias Polynomial for a type PolyNode that has not yet been fully declared
struct PolyNode{
int coef; //coefficient
int expon; //index
Polynomial link; //Pointer to the next domain (declare link, type Polynomial, Polynomial represents an alias for the structure)
};
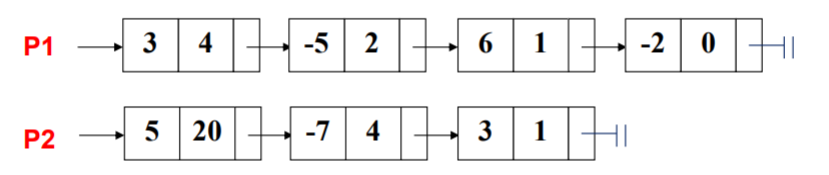
2. Procedural Framework
int main()
{
Polynomial P1,P2,PP,PS;
//Reading polynomial 1, P1 and P2 are pointers to linked list structure
P1=ReadPoly();
//Read in Polynomial 2
P2=ReadPoly();
//Multiplication operation and output, return is also pointer
PP=Mult(P1,P2);
PrintPoly(PP);
//Addition operation and output
PS=Add(P1,P2);
PrintPoly(PS);
return 0;
}
3. Read polynomials
How many items should be input first, then a pair of input coefficients and indices, separated by spaces in the middle?
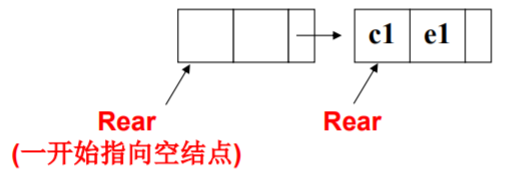
What is the initial value of Rear?
Two treatment methods:
- The initial value of Rear is NULL, which is treated differently in Attach function according to whether Rear is NULL or not.
- Rear points to an empty node and then deletes the empty node (more consistent)
Polynomial ReadPoly()
{
Polynomial P,Rear,t;
int c,e,N;
//Read in an integer first
scanf("%d",&N);
//Head empty node of list
P=(Polynomial)malloc(sizeof(struct PolyNode));
P->link=NULL;
Rear=P;
//Another pair of reading coefficient indices
while(N--)
{
scanf("%d %d",&c,&e);
//Each read-in node is inserted behind the current result expression. rear changes, so pass the pointer
Attach(c,e,&Rear);
}
//Delete temporarily generated header nodes
t=P;
P=P->link;
free(t);
return P;
}
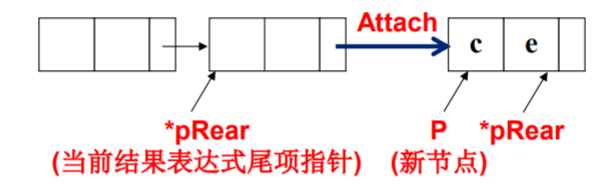

//Pointer of afferent coefficients, exponents, Polynomial types (Polynomial itself is also a pointer)
void Attach(int c,int e,Polynomial *pRear)
{
Polynomial P;
//To apply for a new node, the node type is PolyNode
P=(Polynomial)malloc(sizeof(struct PolyNode));
//Assignment of new nodes
P->coef=c;
P->expon=e;
P->link=NULL;
(*pRear)->link=P;
*pRear=P; //Modify the value of pRear
}
4. Additive Realization
int compare(int e1,int e2){
if(e1>e2) return 1;
else if(e1<e2) return -1;
else return 0;
}
Polynomial Add(Polynomial P1,Polynomial P2){
Polynomial PS,rear,temp;
int sum;
//Construct empty nodes, rear pointing to the tail of the current processing result
PS=(Polynomial)malloc(sizeof(struct PolyNode));
PS->link=NULL;
rear=PS;
while(P1&&P2){
switch(compare(P1->expon,P2->expon)){
case 1:
Attach(P1->coef,P1->expon,&rear);
P1=P1->link;
break;
case -1:
Attach(P2->coef,P2->expon,&rear);
P2=P2->link;
break;
case 0:
sum=P1->coef+P2->coef;
if(sum) Attach(sum,P1->expon,&rear);//coef=0 then do nothing
P1=P1->link;
P2=P2->link;
break;
}
}
while(P1){
Attach(P1->coef,P1->expon,&rear);
P1=P1->link;
}
while(P2){
Attach(P2->coef,P2->expon,&rear);
P2=P2->link;
}
//rear->link=NULL;
temp=PS;
PS=PS->link;
free(temp);
return PS;
}
5. Multiplication Implementation
Multiply the current item of P1 (c1i,e1i) by the current item of P2 (c2i,e2i) and insert it into the result polynomial. The key is to find the insertion location (exponential decline is required)
Initial result polynomials can be obtained by multiplying the first term of P1 by P2 (as above)
Polynomial Mult(Polynomial P1,Polynomial P2)
{
Polynomial P,Rear,t1,t2,t;
int c,e;
//Multiply P1 and P2 and return null as long as one is empty.
if(!P1||!P2) return NULL;
t1=P1;
t2=P2;
//Application for Empty Node
P=(Polynomial)malloc(sizeof(struct PolyNode));
P->link=NULL;
Rear=P;
//First multiply the first term of P1 by P2 to get P
while(t2){
Attach(t1->coef*t2->coef,t1->expon+t2->expon,&Rear);
t2=t2->link; //t2 moves backwards
}
t1=t1->link;
//Double Cycle t1 Each Item Multiplied t2 Each Item
while(t1){
t2=P2;
Rear=P; //Rear initially points to P
while(t2){
e=t1->expon+t2->expon; //Index adds up to get the current index
c=t1->coef*t2->coef; //Multiplication of coefficients to obtain current coefficients
//Find the insertion position. Compare the index and interpolate the current result into the result polynomial in descending order.
while(Rear->link&&Rear->link->expon>e) //The next index of Rear is larger than the index to be inserted, so the rear has to move backwards.
Rear=Rear->link;
if(Rear->link&&Rear->link->expon==e){ //Rear's next index equals the index to be inserted and merged
if(Rear->link->coef+c) //When the coefficients are added together, they are not equal to 0. c is added to the original.
Rear->link->coef+=c;
else{ //When the coefficients are added up, they are equal to 0 and deleted.
t=Rear->link;
Rear->link=t->link;
free(t);
}
}else{ //Rear's next index is smaller than the index to be inserted, and can be inserted
t=(Polynomial)malloc(sizeof(struct PolyNode)); //Apply for a new node
t->coef=c;t->expon=e;
t->link=Rear->link; //Insert a new node
Rear->link=t;Rear=Rear->link;
}
t2=t2->link;
}
t1=t1->link;
}
//The first empty node should be deleted
t2=P;
P=P->link; //Point to the next position
free(t2);
return P;
}
6. Polynomial Output
List traversal
void PrintPoly(Polynomial P)
{ /* Output polynomial */
int flag = 0; /* Auxiliary adjustment of output format */
if (!P) {
printf("0 0\n");
return;
}
while (P) {
if (!flag)
flag = 1;
else
printf(" ");
printf("%d %d", P->coef, P->expon);
P = P->link;
}
printf("\n");
}
Operation results