What is Morris traversal

For general traversal algorithms, we use stacks to store the nodes that need to be accessed again. In the worst case, we need to store the entire binary tree node. So the space complexity is O(n). Morris traversal reduces the spatial complexity to the O(1) level. Morris traversal uses the concept of "clue binary tree", in fact, it uses the left and right empty pointers of leaf nodes to store some traversal precursor or successor nodes. So no extra space was used.

Algorithm idea of Morris traversal

Assume that the current node is cur and is initially assigned root.

1. Judge whether the cur node is empty
2. If not empty
   1) If cur has no left child, cur updates to the right, that is, (cur = cur.right)
   2) If cur has left children, find the rightmost node pre from the left subtree
   • If the right child of pre is empty, point the right child to cur. pre.right = cur
   • If the right child of pre is cur, point it to null. pre.right = null. (restore tree structure)
3. Stop traversal when cur is empty

Morris preorder traversal

Let's take a simple binary tree as an example to illustrate the process of Morris pre traversal.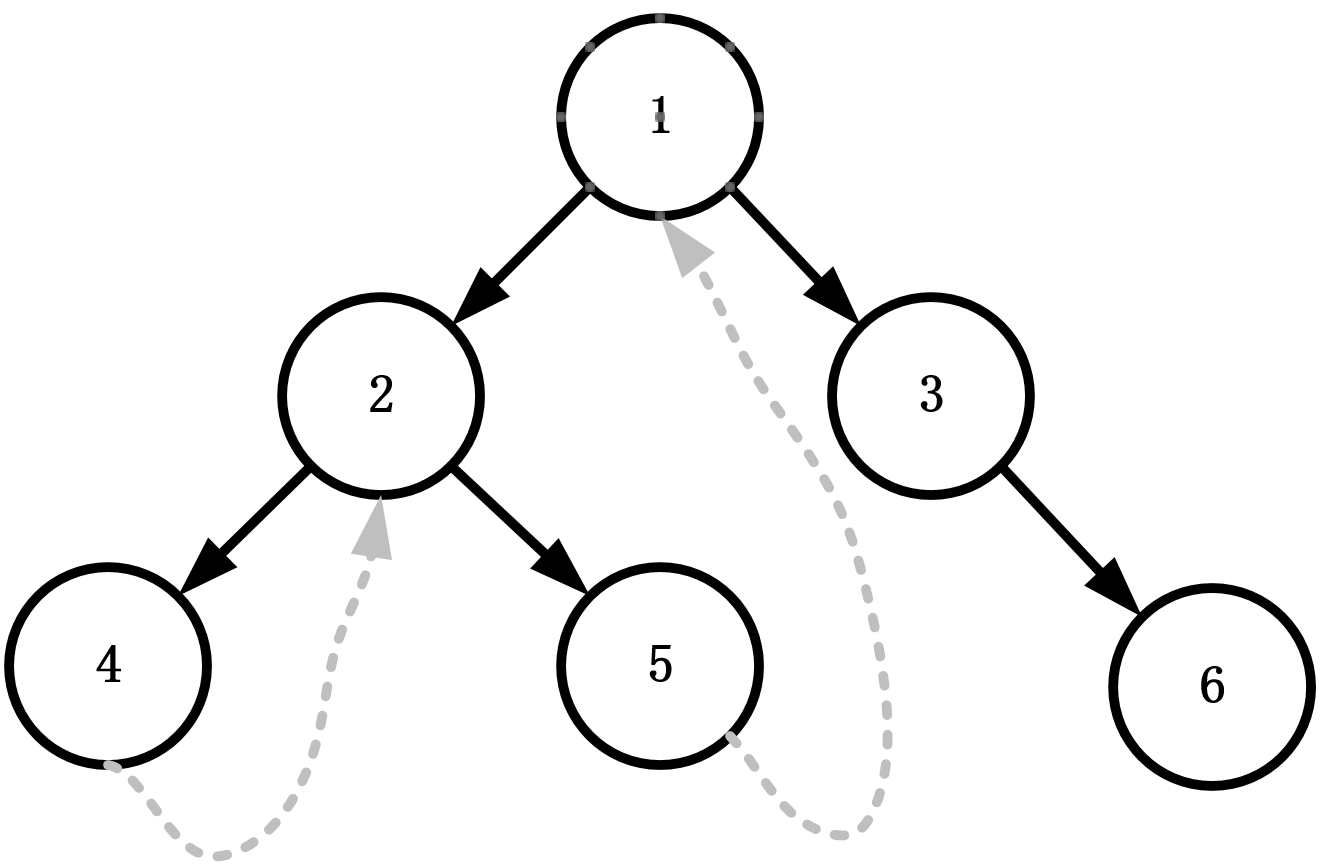

• Set root node 1 to cur.
• Because cur (node 1) is not empty, and the left child node 2 of cur (node 1) is not empty, we find the rightmost node 5 in the left subtree with node 2 as the root node.
• The right child of node 5 is empty. At this time, we output the value of cur (node 1), and then point the right child of node 5 to cur, that is, node 1. Update cur node to cur left child, which is node 2.
• Because the left child of cur (node 2) is not empty, find the rightmost node 4 of its left subtree
• The right child of node 4 is empty. First output the value of cur (node 2), then point the right child of node 4 to cur (node 2), and update cur (node 2) to its left child node 4.
• At this time, the left child of cur (node 4) is empty, so visit its right child and find that the right child points to node 2, so we update cur to node 2.
• At this time, we found that cur also points to node 2, so left child node 4 is not empty. We found the rightmost node 4 in the left subtree again, but at this time, the right child of node 4 points to cur, so we deleted it, that is, the right child of node 4 points to empty, and restored the original tree structure. And since the left child and root node have been accessed, we will visit the right child node 5 at this time.
• ...

public void Morris_preorderTraversal(TreeNode root){
    TreeNode cur = root;
    while(cur!=null){
        if(cur.left!=null){
            TreeNode pre = cur.left;
            while(pre.right!=null && pre.right!=cur){
                pre = pre.right;
            }
            if(pre.right == null){	// First arriving at the right end of the left subtree
                System.out.print(cur.val);
                pre.right = cur;
                cur = cur.left;
            }
            else{ // The second time to the right end of the left subtree
                pre.right = null;
                cur = cur.right;
            }
        }
        else{
            System.out.print(cur.val);
            cur = cur.right;
        }
    }
}

Morris middle order traversal

In Morris, there is no significant difference between sequence traversal and preorder traversal, but there is a change in the output position.

public void Morris_inorderTraversal(TreeNode root){
        TreeNode cur = root;
        while(cur!=null){
            if(cur.left!=null){
                TreeNode pre = cur.left;
                while(pre.right!=null && pre.right!=cur){
                    pre = pre.right;
                }
                if(pre.right == null){
                    pre.right = cur;
                    cur = cur.left;
                }
                else{
                    pre.right = null;
                    System.out.print(cur.val);
                    cur = cur.right;
                }
            }
            else {
                System.out.print(cur.val);
                cur = cur.right;
            }
        }
    }

Morris postorder traversal

Morris postorder traversal is also the most complex one. Because the right child needs to output before the root node. For the following figure, the sequence of subsequent traversal is: 4, 5, 2, 6, 3, 1. We can see that for the left subtree of node 1, node 2 and node 5 are the right boundaries. As long as we output in reverse order, we can achieve the access order of the subsequent traversal. Therefore, we need a function to reverse it, that is, node 5 points to node 2. And after the output, it is reversed (without changing the structure of the tree).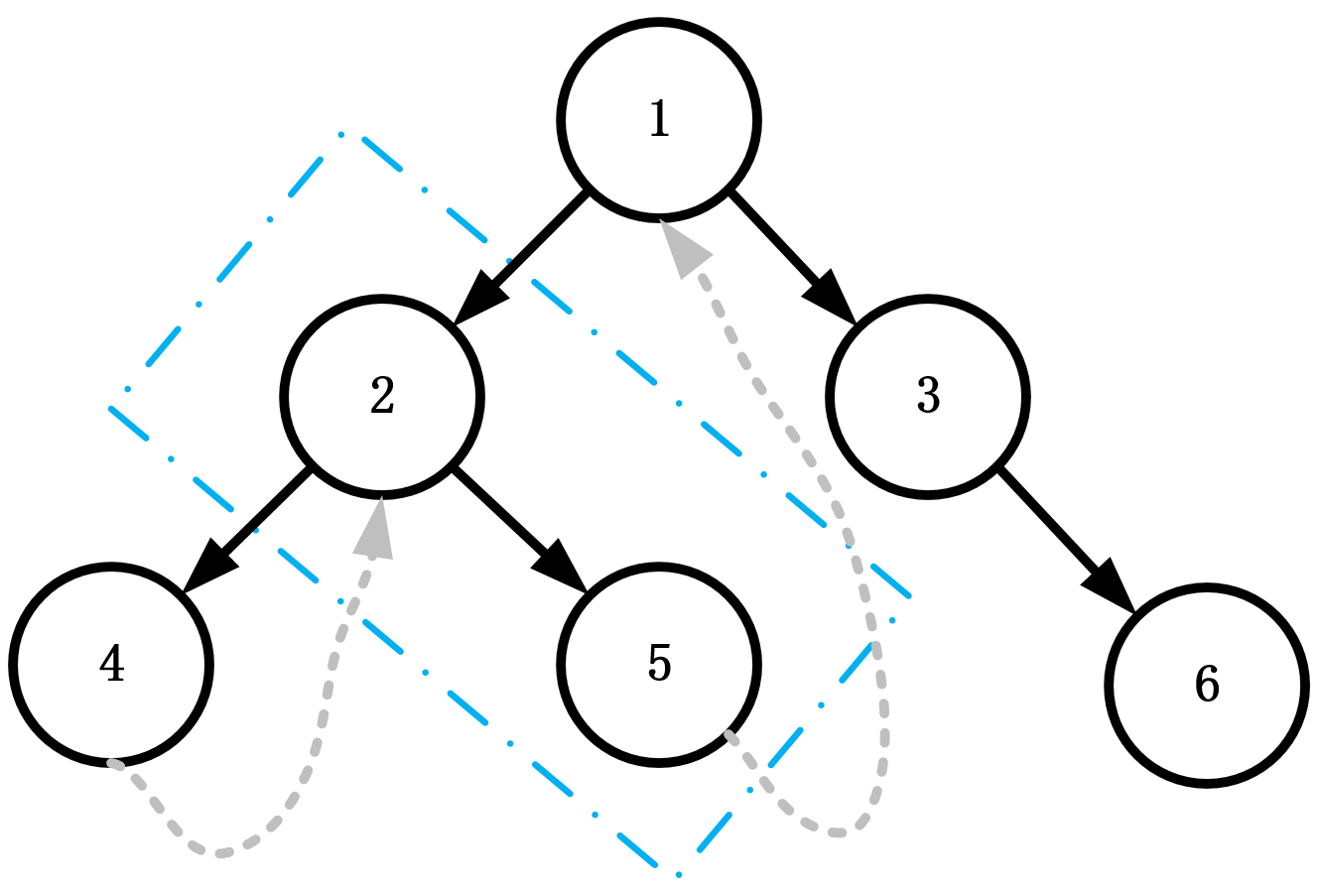

public TreeNode reverseNode(TreeNode node){
    TreeNode pre = null;
    TreeNode next = null;
    while(node!=null){
        next = node.right;
        node.right = pre;
        pre = node;
        node = next;
    }
    return pre;
}

public void printNode(TreeNode node){
    TreeNode tail = reverseNode(node);
    TreeNode cur = tail;
    while(cur!=null){
        System.out.println(cur.val);
        cur = cur.right;
    }
    reverseNode(tail);
}

public void Morris_postorderTraversal(TreeNode root) {
    TreeNode cur = root;
    while(cur != null){
        if(cur.left!=null){
            TreeNode pre = cur.left;
            while(pre.right!=null && pre.right!=cur){
                pre = pre.right;
            }
            if(pre.right==null){
                pre.right = cur;
                cur = cur.left;
            }
            else{
                pre.right = null;
                printNode(cur.left);
                cur = cur.right;
            }
        }
        else{
            cur = cur.right;
        }
    }
    printNode(root);
}

summary

Morris traversal reduces the spatial complexity of binary tree traversal to O(1), while the time complexity is still O(n).