Experiment time: 11.10
catalogue
Generating complete binary tree
Implementation of Morris algorithm
Introduction to morris traversal
Implementation principle of morris traversal
The essence of morris traversal
Briefly describe the algorithm process
Experimental results (including time, space and output results):
Generating complete binary tree
Just use queue generation.
//Using queues, a complete binary tree is generated
void CreateTreeNode(TreeNode *root, int Num) {
queue<TreeNode *> Q;
Q.push(root);//Root node join
int data = 1;//The value of the root is 1
while (data < Num) {
TreeNode *curr_node = Q.front();//Take the first element of the team
Q.pop();//Team first team
curr_node->left = new TreeNode;
curr_node->left->val = data++;
Q.push(curr_node->left);//Left subtree at the end of the team
curr_node->right = new TreeNode;
curr_node->right->val = data++;
Q.push(curr_node->right);//Right subtree at the end of the team
}
}Implementation of Morris algorithm
Reference here Divine traversal - morris - Zhihu (zhihu.com)
Introduction to morris traversal
morris traversal is a super advanced algorithm of binary tree traversal algorithm, which follows the spatial complexity of recursive and non recursive (stack implementation). morris traversal can reduce the spatial complexity of non recursive traversal to O(1). Thus, a sophisticated algorithm with time complexity of O(N) and space complexity of O(1) is realized.morris traversal uses that the left and right children of the leaf nodes of the tree are empty (a large number of free pointers of the tree), so as to reduce the space overhead to the limit.
Implementation principle of morris traversal
Record the current node as cur.
- If cur has no left child, cur moves to the right (cur=cur.right)
- If cur has left children, find the rightmost node on cur's left subtree and record it as most right
- If the right pointer of mostright points to null, let it point to cur, and cur moves to the left (cur=cur.left)
- If the right pointer of mostright points to cur, let it point to null, and cur moves to the right (cur=cur.right)
Implement the above principles, that is, morris traversal.
The essence of morris traversal
Establish a mechanism for Nodes without a left subtree arrive only once, and nodes with a left subtree arrive twiceBriefly describe the algorithm process
Cur is the current node, and next is used for the rightmost node in the left subtree of cur
while (cur is not empty)
If cur - > left is empty
Output cur - > val
Cur points to cur - > right
else
next points to cur - > left
Wihile next - > right is not null and not equal to cur
Next points to next - > right
If next - > right is empty, it indicates that the node is reached for the first time
Next - > right points to cur
If the preamble traverses, the value of cur is output here
else indicates the second arrival at the node
Next - > right is set to NULL
If it is traversed in middle order, the value of cur is output here
After traversal, all the nodes in the rightmost column of cur - > left can be output
Cur points to cur - > right
For post order traversal, you also need to output all the nodes in the rightmost column of the root node head
//Output the nodes in the rightmost column of temp in reverse order
void ReverserPrint(TreeNode *temp) {
stack<int> tempList;
while (temp) {//Put all the right child nodes of the current node into the stack
tempList.push(temp->val);
temp = temp->right;
}
while (!tempList.empty()) {//Output stack elements
cout << setw(4) << tempList.top();
tempList.pop();
}
}
//Traversal binary tree implemented by Morris
//flag 1 2 3 corresponds to the first order, middle order and last order traversal
void MorrisTraversal(TreeNode *head, const int &flag) {
//next is used to find the rightmost node of the cur left subtree of the current node
TreeNode *next = NULL, *cur = head;
//Until the node is empty
while (cur) {
//Judge whether the left subtree of the current node is empty. If it is empty, the current node will be output
if (!cur->left) {
if (flag != 3) {
cout << setw(4) << cur->val;
}
cur = cur->right;//The current node cur points to the right subtree
} else {//The left subtree of the current node is not empty
//Find the rightmost node of the left subtree and point to the current node cur
next = cur->left;
while (next->right && next->right != cur) {//If the node is empty or cur, the loop ends
next = next->right;
}
//The first arrival is null, pointing to cur
if (!next->right) {
if (flag == 1) {//Preorder traversal
cout << setw(4) << cur->val;
}
next->right = cur;//cur pointing to current node
cur = cur->left;//Point to right subtree
} else {//Second arrival, recovery
next->right = NULL;//Leave blank
if (flag == 2) {//Medium order traversal
cout << setw(4) << cur->val;
}
if (flag == 3) {//In subsequent traversal, the rightmost column of cur - > left is output in reverse order
ReverserPrint(cur->left);
}
cur = cur->right;//Point to right subtree
}
}
}
if (flag == 3) {//Output the rightmost column of the last head node
ReverserPrint(head);
}
}Recursive implementation
//Traversal of recursive implementation
//flag 1 2 3 corresponds to the first order, middle order and last order traversal
void RecursiveTraversal(TreeNode *Node, const int &flag) {
if (Node != NULL) {
if (flag == 1) {
cout << setw(4) << Node->val;
}
RecursiveTraversal(Node->left, flag);
if (flag == 2) {
cout << setw(4) << Node->val;
}
RecursiveTraversal(Node->right, flag);
if (flag == 3) {
cout << setw(4) << Node->val;
}
}
}Experimental results (including time, space and output results):
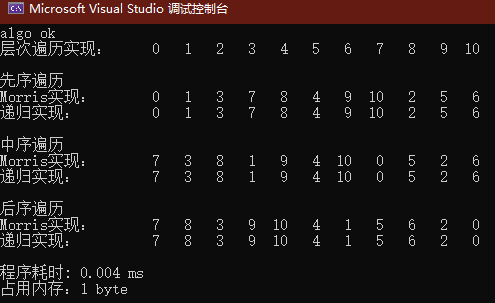
source code
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
#include<ctime>
#include<iomanip>
using namespace std;
struct TreeNode {
int val = 0;
TreeNode *left = NULL;
TreeNode *right = NULL;
};
//Using queues, a complete binary tree is generated
void CreateTreeNode(TreeNode *root, int Num) {
queue<TreeNode *> Q;
Q.push(root);//Root node join
int data = 1;//The value of the root is 1
while (data < Num) {
TreeNode *curr_node = Q.front();//Take the first element of the team
Q.pop();//Team first team
curr_node->left = new TreeNode;
curr_node->left->val = data++;
Q.push(curr_node->left);//Left subtree at the end of the team
curr_node->right = new TreeNode;
curr_node->right->val = data++;
Q.push(curr_node->right);//Right subtree at the end of the team
}
}
//Using the queue, the binary tree is traversed hierarchically
void LevelOrderTraversal(TreeNode *root) {
queue<TreeNode *> Q;
Q.push(root);//Root node queue
while (!Q.empty()) {//If the queue is not empty, it will be traversed all the time
TreeNode *curr_node = Q.front();//Take the first element of the team
cout<< setw(4) << curr_node->val;//Outputs the value of the current element
Q.pop();//Team first team
if (curr_node->left) {//Left subtree is not empty
Q.push(curr_node->left);//Left subtree at the end of the team
}
if (curr_node->right) {//ditto
Q.push(curr_node->right);
}
}
}
//Traversal of recursive implementation
//flag 1 2 3 corresponds to the first order, middle order and last order traversal
void RecursiveTraversal(TreeNode *Node, const int &flag) {
if (Node != NULL) {
if (flag == 1) {
cout << setw(4) << Node->val;
}
RecursiveTraversal(Node->left, flag);
if (flag == 2) {
cout << setw(4) << Node->val;
}
RecursiveTraversal(Node->right, flag);
if (flag == 3) {
cout << setw(4) << Node->val;
}
}
}
//Output the nodes in the rightmost column of temp in reverse order
void ReverserPrint(TreeNode *temp) {
stack<int> tempList;
while (temp) {//Put all the right child nodes of the current node into the stack
tempList.push(temp->val);
temp = temp->right;
}
while (!tempList.empty()) {//Output stack elements
cout << setw(4) << tempList.top();
tempList.pop();
}
}
//Traversal binary tree implemented by Morris
//flag 1 2 3 corresponds to the first order, middle order and last order traversal
void MorrisTraversal(TreeNode *head, const int &flag) {
//next is used to find the rightmost node of the cur left subtree of the current node
TreeNode *next = NULL, *cur = head;
//Until the node is empty
while (cur) {
//Judge whether the left subtree of the current node is empty. If it is empty, the current node will be output
if (!cur->left) {
if (flag != 3) {
cout << setw(4) << cur->val;
}
cur = cur->right;//The current node cur points to the right subtree
} else {//The left subtree of the current node is not empty
//Find the rightmost node of the left subtree and point to the current node cur
next = cur->left;
while (next->right && next->right != cur) {//If the node is empty or cur, the loop ends
next = next->right;
}
//The first arrival is null, pointing to cur
if (!next->right) {
if (flag == 1) {//Preorder traversal
cout << setw(4) << cur->val;
}
next->right = cur;//cur pointing to current node
cur = cur->left;//Point to right subtree
} else {//Second arrival, recovery
next->right = NULL;//Leave blank
if (flag == 2) {//Medium order traversal
cout << setw(4) << cur->val;
}
if (flag == 3) {//In subsequent traversal, the rightmost column of cur - > left is output in reverse order
ReverserPrint(cur->left);
}
cur = cur->right;//Point to right subtree
}
}
}
if (flag == 3) {//Output the rightmost column of the last head node
ReverserPrint(head);
}
}
// All code needs to be written in the Algo class to define other required variables or functions
class Algo {
public:
Algo() {
cout << "algo ok" << endl;
}
int run(TreeNode *head) {
//Write your code here
cout << "Hierarchical traversal implementation:\t";
LevelOrderTraversal(head);
for (auto i = 1; i <= 3; ++i) {
if (i == 1) {
cout <<"\n\n Preorder traversal \nMorris realization:\t";
MorrisTraversal(head, i);
cout << "\n Recursive implementation:\t";
RecursiveTraversal(head, i);
} else if (i == 2) {
cout << "Medium order traversal\nMorris realization:\t";
MorrisTraversal(head, i);
cout << "\n Recursive implementation:\t";
RecursiveTraversal(head, i);
} else if (i == 3) {
cout << "Postorder traversal\nMorris realization:\t";
MorrisTraversal(head, i);
cout<< "\n Recursive implementation:\t";
RecursiveTraversal(head, i);
}
cout << "\n\n";
}
return 0; //Modify to return the correct result
}
};
int main() {
Algo algo;
TreeNode head;
CreateTreeNode(&head, 10); //10 is the number of generated binary tree nodes, and the generated binary tree is a complete binary tree
time_t start = clock();
algo.run(&head);
time_t end = clock();
cout << "Program time: " << double(end - start) / CLOCKS_PER_SEC << " ms" << endl;
cout << "Occupied memory:" << sizeof(algo) << " byte" << endl;
return 0;
}