describe
The railway connection structure of a train dispatching station is shown in Figure 1

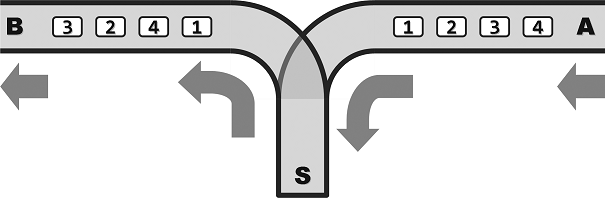
Where, A is the inlet, B is the outlet, and S is the transfer blind end. All railways are single track one-way: the train can only travel from A to s, and then from s to B; in addition, overtaking is not allowed. Because cars can reside in s, the order in which they exit from B may be different from the order in which they enter from A. However, the capacity of S is limited, and the number of cars that can stay at the same time shall not exceed m.
Suppose that the number of a train is {1, 2 , n}. The dispatcher would like to know whether these cars can be equipped with {a1, a2 The order of an} is rearranged and drives out from the B end. If so, in what order?

input
A total of two lines.

The first line is two integers n, m.

The second line is n integers separated by spaces, guaranteed to be {1, 2 A permutation of, n} that represents the exit sequence {a1, a2,... To be judged as feasible an}.

output
If the exit sequence is feasible, the operation sequence will be output, where push indicates that the car enters S from A, pop indicates that the car enters B from S, and each operation takes one line.

If not, output No.

Example
Example 1
Input

5 2
1 2 3 5 4
Output

push
pop
push
pop
push
pop
push
push
pop
pop
Example 2
Input

5 5
3 1 2 4 5
Output

No

limit
1 ≤ n ≤ 1,600,000

0 ≤ m ≤ 1,600,000

Time: 2 sec

Space: 256 MB

The code is as follows

#include<cstdio>
#include<string.h>
const int maxn = 16e5 + 5;

struct stack
{
    int n = 0;
    int ss[maxn];

    void push(int a)
    {
        n++;
        ss[n] = a;
    }
    void pop()
    {
        n--;
    }
    int top()
    {
        return ss[n];
    }
    bool empty()
    {
        if(n == 0)return true;
        else return false;
    }
    int size()
    {
        return n;
    }
};

stack  a;
stack  s;
stack  b;
bool way[maxn];
int total[maxn];
int main()
{
    int m, n;
    scanf("%d%d", &n, &m);
    for(int i = n; i >= 1; i--)
    {
        a.push(i);
    }
    for(int i = 0; i < n; i++)
        scanf("%d", &total[i]);
    int j = 0, k = 0;
    bool y = false;
    while(!y)
    {
        if(k == n){y = true; break;}
        if(s.empty())
        {
            s.push(a.top());
            a.pop();
            way[j] = true;
        }
        else if(total[k] == s.top())
        {
            b.push(s.top());
            s.pop();
            k++;
            way[j] = false;
        }
        else if(!a.empty())
        {
            s.push(a.top());
            a.pop();
            way[j] = true;
        }
        else
        {
            printf("No\n");
            break;
        }
        if(s.size() > m)
        {
            printf("No\n");
            break;
        }
        j++;
    }
    if(y)
    {
        for(int i = 0; i < j; i++)
        {
            if(way[i]) printf("push\n");
            else printf("pop\n");
        }
    }
    return 0;
}

final result

Case No.    Result  Time(ms)    Memory(KB)
1   Accepted    0   39000
2   Accepted    0   39000
3   Accepted    0   39000
4   Accepted    0   39000
5   Accepted    0   39000
6   Accepted    0   39000
7   Accepted    0   39000
8   Accepted    0   39000
9   Accepted    0   39000
10  Accepted    0   39000
11  Accepted    4   39000
12  Accepted    8   39000
13  Accepted    20  39000
14  Accepted    40  39000
15  Accepted    32  39000
16  Accepted    12  39000
17  Accepted    96  39000
18  Wrong Answer    292 39000
19  Wrong Answer    352 39000
20  Wrong Answer    328 39000

The simple simulation of stack operation takes a little space. Unfortunately, the last three use cases can't be passed. At present, I don't think of the reason. I hope someone can help me to have a look. Thank you.