1, Experimental overview
lab5 is mainly used to realize the B + tree index. It mainly has the functions of query, insertion and deletion. The query is mainly based on the characteristics of B + tree. The splitting of nodes should be considered for insertion (when the node tuples are full), the redistribution of elements in nodes should be considered for deletion (when a page is empty and the adjacent pages are full), and the merging of sibling nodes (when the elements of two adjacent pages are empty), the above is the general content of this experiment.
In this lab you will implement a B+ tree index for efficient lookups and range
scans. We supply you with all of the low-level code you will need to implement
the tree structure. You will implement searching, splitting pages,
redistributing tuples between pages, and merging pages.
(find, split pages, reassign tuples, merge pages)
You may find it helpful to review sections 10.3–10.7 in the textbook, which
provide detailed information about the structure of B+ trees as well as
pseudocode for searches, inserts and deletes.
As described by the textbook and discussed in class, the internal nodes in B+
trees contain multiple entries, each consisting of a key value and a left and a
right child pointer. Adjacent keys share a child pointer, so internal nodes
containing m keys have m+1 child pointers. Leaf nodes can either contain
data entries or pointers to data entries in other database files. For
simplicity, we will implement a B+tree in which the leaf pages actually contain
the data entries. Adjacent leaf pages are linked together with right and left
sibling pointers, so range scans only require one initial search through the
root and internal nodes to find the first leaf page. Subsequent leaf pages are
found by following right (or left) sibling pointers.
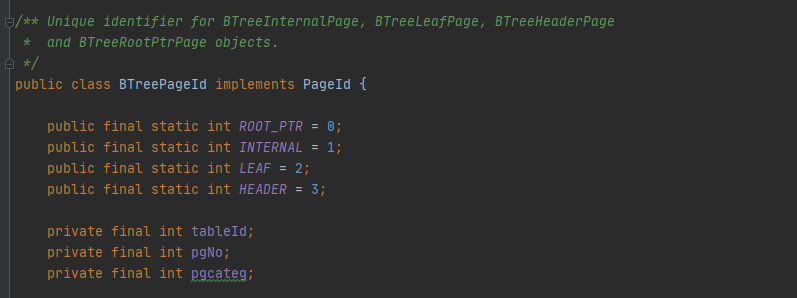
Before the experiment, we need to clarify the structure of the whole B + tree. There are four types of page nodes of B +:
1. Root node page: the root node of a B + tree, which is implemented as BTreeRootPtrPage.java in SimpleDB;
2. Internal node page: nodes other than root nodes and leaf nodes are implemented as btreeinternalpages in SimpleDB. Each BTreeInternalPage consists of one entry;
3. Leaf node page: stores the leaf node of tuple, which is implemented as BTreeLeafPage in SimpleDB;
4. Header node page: used to record the usage of a page in the whole B + tree. It is implemented as BTreeHeaderPage in SimpleDB.
At the same time, the four pages are distinguished by PageId:
2, Experimental process
1.Search
Given a field and a page, recursively find the leaf node of tuple from this page.
Your first job is to implement the findLeafPage() function in
BTreeFile.java. This function is used to find the appropriate leaf page given
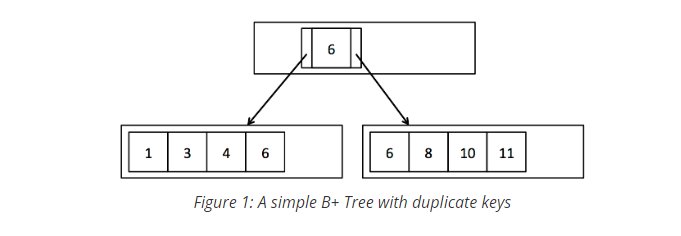
a particular key value, and is used for both searches and inserts. For example,
suppose we have a B+Tree with two leaf pages (See Figure 1). The root node is an
internal page with one entry containing one key (6, in this case) and two child
pointers. Given a value of 1, this function should return the first leaf page.
Likewise, given a value of 8, this function should return the second page. The
less obvious case is if we are given a key value of 6. There may be duplicate
keys, so there could be 6's on both leaf pages. In this case, the function
should return the first (left) leaf page.
Exercise 1: BTreeFile.findLeafPage()
Implement BTreeFile.findLeafPage().
After completing this exercise, you should be able to pass all the unit tests
in BTreeFileReadTest.java and the system tests in BTreeScanTest.java.
This part is mainly based on the tips of the handout. The main implementation ideas are as follows:
1. Obtain data page type;
2. Judge whether the data page is a leaf node. If so, the recursion ends and the page is returned;
3. If not, it indicates that the page is an internal node, and the page type is converted;
4. Obtain the iterator of the internal node;
5. Iterate the entry of the internal node. Here, the main processing is that the field is empty. If it is empty, just find the leftmost leaf page directly;
6. Find the first entry greater than (or equal to) filed, and then recurse its left child;
7. If you get to the last page, recurse its right child;
Here, we need to have some concepts about the search process of B + tree, and then we should also pay attention to the control of read-write permission. According to this permission, the transactions implemented by lab4 will add different locks. The implementation code is as follows:
private BTreeLeafPage findLeafPage(TransactionId tid, Map<PageId, Page> dirtypages, BTreePageId pid, Permissions perm,
Field f)
throws DbException, TransactionAbortedException {
// some code goes here
//1. Get data page type
int type = pid.pgcateg();
//2. If it is a leaf page, the recursion ends, indicating that it is found
if (type == BTreePageId.LEAF) return (BTreeLeafPage)getPage(tid, dirtypages, pid, perm);
//3. READ_ONLY perm is used to read the internal page
BTreeInternalPage internalPage = (BTreeInternalPage)getPage(tid, dirtypages, pid, Permissions.READ_ONLY);
//4. Get the entries of this page
Iterator<BTreeEntry> it = internalPage.iterator();
//Here, you need to declare the entry outside the loop. If the last entry is not found, return the right child of the last entry
BTreeEntry entry = null;
while (it.hasNext()) {
entry = it.next();
if (f == null) return findLeafPage(tid, dirtypages, entry.getLeftChild(), perm, f);
Field key = entry.getKey();
if (key.compare(Op.GREATER_THAN_OR_EQ, f)) return findLeafPage(tid, dirtypages, entry.getLeftChild(), perm, f);
}
return findLeafPage(tid, dirtypages, entry.getRightChild(), perm, f);
}
Test case:
B + tree index lookup process:
1. Create an operator because the B + tree only supports single column indexes. The operators are greater than, less than, equal to, greater than or equal to, less than or equal to, not equal to:
IndexPredicate ipred = new IndexPredicate(Op.GREATER_THAN, f);
2. Call the indexIterator method of BTreeFile to obtain the search result. The indexIterator method will create the BTreeSearchIterator iterator:
DbFileIterator it = twoLeafPageFile.indexIterator(tid, ipred);
public DbFileIterator indexIterator(TransactionId tid, IndexPredicate ipred) {
return new BTreeSearchIterator(this, tid, ipred);
}
3. When the search result needs to be obtained, the open and getnext methods of BTreeSearchIterator will be called to obtain the query result:
4. First, open and open the iterator. First, get the page from getPage, where the lock will be added, and then the first call will be from BTreeFile.getPage() Get the root node, because when writing a file, the root node is written according to the type of internal node, and then each root node has 9 entries. The first traversal actually traverses the 9 entries of the root node, and then looks down. Of course, this is only to find the leaf node page and create an iterator. The real search is in the next step.
public void open() throws DbException, TransactionAbortedException {
BTreeRootPtrPage rootPtr = (BTreeRootPtrPage) Database.getBufferPool().getPage(
tid, BTreeRootPtrPage.getId(f.getId()), Permissions.READ_ONLY);
BTreePageId root = rootPtr.getRootId();
if(ipred.getOp() == Op.EQUALS || ipred.getOp() == Op.GREATER_THAN
|| ipred.getOp() == Op.GREATER_THAN_OR_EQ) {
curp = f.findLeafPage(tid, root, ipred.getField());
}
else {
curp = f.findLeafPage(tid, root, null);
}
it = curp.iterator();
}
5. Then, when you want to get the result, call readNext of the iterator, and then get the result according to the operator. Here, during the iteration, you iterate over all tuples of a leaf page, and then filter out the results that meet the operator. For example, if age > 18, you will first find the last entry less than 18, and then get the left child of the entry to get the leaf page, and then Iteratively find tuples with age > 18 in the leaf page. If the leaf page is traversed, it will always find the tuples of the next page in the direction of the right brother, because there is a two-way linked list between multiple leaf pages.
@Override
protected Tuple readNext() throws TransactionAbortedException, DbException,
NoSuchElementException {
while (it != null) {
while (it.hasNext()) {
Tuple t = it.next();
if (t.getField(f.keyField()).compare(ipred.getOp(), ipred.getField())) {
return t;
}
else if(ipred.getOp() == Op.LESS_THAN || ipred.getOp() == Op.LESS_THAN_OR_EQ) {
// if the predicate was not satisfied and the operation is less than, we have
// hit the end
return null;
}
else if(ipred.getOp() == Op.EQUALS &&
t.getField(f.keyField()).compare(Op.GREATER_THAN, ipred.getField())) {
// if the tuple is now greater than the field passed in and the operation
// is equals, we have reached the end
return null;
}
}
BTreePageId nextp = curp.getRightSiblingId();
// if there are no more pages to the right, end the iteration
if(nextp == null) {
return null;
}
else {
curp = (BTreeLeafPage) Database.getBufferPool().getPage(tid,
nextp, Permissions.READ_ONLY);
it = curp.iterator();
}
}
2.Insert
The operation related to insert here was very confused at the beginning. Although we generally know the process, there are still many loopholes in writing code. There are many situations that need to be taken into account, which is a bit like lab4.
In this exercise you will implement splitLeafPage() and splitInternalPage()
in BTreeFile.java. If the page being split is the root page, you will need to
create a new internal node to become the new root page, and update the
BTreeRootPtrPage. Otherwise, you will need to fetch the parent page with
READ_WRITE permissions, recursively split it if necessary, and add a new entry.
You will find the function getParentWithEmptySlots() extremely useful for
handling these different cases. In splitLeafPage() you should "copy" the key
up to the parent page, while in splitInternalPage() you should "push" the key
up to the parent page. See Figure 2 and review section 10.5 in the text book if
this is confusing. Remember to update the parent pointers of the new pages as
needed (for simplicity, we do not show parent pointers in the figures). When an
internal node is split, you will need to update the parent pointers of all the
children that were moved. You may find the function updateParentPointers()
useful for this task. Additionally, remember to update the sibling pointers of
any leaf pages that were split. Finally, return the page into which the new
tuple or entry should be inserted, as indicated by the provided key field.
(Hint: You do not need to worry about the fact that the provided key may
actually fall in the exact center of the tuples/entries to be split. You should
ignore the key during the split, and only use it to determine which of the two
pages to return.)
After the insertion experiment, I feel that I must read the handout carefully. The handout can be said to tell you most of the possible pits and what operations need to be involved. Among them, the getParentWithEmptySlots method is particularly useful to help us consider what will happen if the parent node is also full. In fact, some situations can be judged and considered Recursively call spiltInternalPage to realize the recursive splitting of the parent node. I feel that this part can be completed independently as an exercise. I feed too much food hhh.
Exercise 2: Splitting Pages
Implement BTreeFile.splitLeafPage() and BTreeFile.splitInternalPage().
After completing this exercise, you should be able to pass the unit tests in
BTreeFileInsertTest.java. You should also be able to pass the system tests
in systemtest/BTreeFileInsertTest.java. Some of the system test cases may
take a few seconds to complete. These files will test that your code inserts
tuples and splits pages correcty, and also handles duplicate tuples.
exercise2 needs to implement the two methods of splitting leaf nodes and splitting internal nodes. In fact, the diagram given is also very clear, but it is a little difficult to write code.
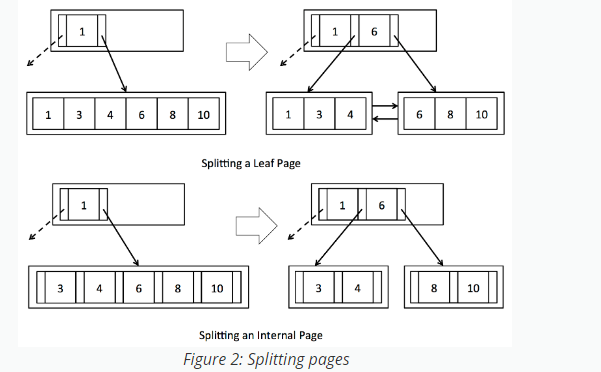
Idea of splitting leaf nodes:
1. Create a new leaf page as a new page;
2. Copy the tuple of the full page to the new page and delete it while copying;
3. Check whether there are right brothers on the previous full page. If so, the pointer needs to be updated. This is a bit like inserting a node in a two-way linked list. It was not considered at the beginning. It was found that the pointer needs to be updated only after the subsequent test cases could not be reorganized;
4. Update dirty pages;
5. Update sibling pointer;
6. Find the parent node, create an entry for insertion, and finally update the dirty page;
7. Find the page to be inserted according to the field and return;
public BTreeLeafPage splitLeafPage(TransactionId tid, Map<PageId, Page> dirtypages, BTreeLeafPage page, Field field)
throws DbException, IOException, TransactionAbortedException {
//1. Create a new empty page
BTreeLeafPage rightPage = (BTreeLeafPage) getEmptyPage(tid, dirtypages, BTreePageId.LEAF);
int total = page.getNumTuples();
int moveCnt = total / 2;
Iterator<Tuple> it = page.reverseIterator();
//2. Copy the tuple of the full page to the new page and delete it
while (moveCnt > 0) {
Tuple t = it.next();
page.deleteTuple(t);
rightPage.insertTuple(t);
moveCnt --;
}
//3. Check whether the original page has a right page, and update the pointer if necessary
BTreePageId rightSiblingId = page.getRightSiblingId();
BTreeLeafPage oldRightPage = rightSiblingId == null ? null : (BTreeLeafPage) getPage(tid, dirtypages, rightSiblingId, Permissions.READ_WRITE);
if (oldRightPage != null) {
oldRightPage.setLeftSiblingId(rightPage.getId());
rightPage.setRightSiblingId(oldRightPage.getId());
dirtypages.put(oldRightPage.pid, oldRightPage);
}
//4. Update dirty page
dirtypages.put(page.pid, page);
dirtypages.put(rightPage.pid, rightPage);
//5. Update sibling pointer
page.setRightSiblingId(rightPage.getId());
rightPage.setLeftSiblingId(page.getId());
//Find the parent node and create an entry for insertion, and finally mark the dirty page
BTreeInternalPage parent = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), field);
Field mid = it.next().getField(parent.keyField);
BTreeEntry entry = new BTreeEntry(mid, page.pid, rightPage.pid);
parent.insertEntry(entry);
dirtypages.put(parent.pid, parent);
//Update pointer
updateParentPointer(tid, dirtypages, parent.pid, page.pid);
updateParentPointer(tid, dirtypages, parent.pid, rightPage.pid);
boolean right = field.compare(Op.GREATER_THAN, mid);
return right ? rightPage : page;
}
Idea of splitting internal nodes:
1. Create an internal page as a new page;
2. Copy the entry of the full page to the new page and delete it while copying;
3. Squeeze out the intermediate nodes. This is different from the leaf page. Note that the difference can be found by looking at the figure;
4. Update dirty pages;
5. Update the left and right child pointers;
6. Update the child pointers on the left and right leaf surfaces because there are a large number of entries inserted and removed in front;
7. Obtain the parent node according to the intermediate node, insert the midEntry into the parent node, and update the dirty page and pointer;
8. Find the page to be inserted according to the field and return;
public BTreeInternalPage splitInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage page, Field field)
throws DbException, IOException, TransactionAbortedException {
// some code goes here
//
// Split the internal page by adding a new page on the right of the existing
// page and moving half of the entries to the new page. Push the middle key up
// into the parent page, and recursively split the parent as needed to accommodate
// the new entry. getParentWithEmtpySlots() will be useful here. Don't forget to update
// the parent pointers of all the children moving to the new page. updateParentPointers()
// will be useful here. Return the page into which an entry with the given key field
// should be inserted.
//1. Create a new empty page
BTreeInternalPage rightPage = (BTreeInternalPage)getEmptyPage(tid, dirtypages, BTreePageId.INTERNAL);
int total = page.getNumEntries();
int moveCnt = total / 2;
Iterator<BTreeEntry> it = page.reverseIterator();
//2. Copy the entry to the new page
while (moveCnt > 0) {
BTreeEntry e = it.next();
page.deleteKeyAndRightChild(e);
rightPage.insertEntry(e);
// rightPage.updateEntry(e);
moveCnt --;
}
//3. Squeeze out the intermediate nodes
BTreeEntry midEntry = it.next();
page.deleteKeyAndRightChild(midEntry);
//4. Update dirty page
dirtypages.put(page.pid, page);
dirtypages.put(rightPage.pid, rightPage);
//5. Update the left and right child pointers
midEntry.setLeftChild(page.pid);
midEntry.setRightChild(rightPage.pid);
//6. Update the child pointers on the left and right leaf surfaces because there are a large number of entries inserted and removed in front
updateParentPointers(tid, dirtypages, page);
updateParentPointers(tid, dirtypages, rightPage);
//7. Obtain the parent node according to the intermediate node, insert the midEntry into the parent node, and update the dirty page and pointer
BTreeInternalPage parent = getParentWithEmptySlots(tid, dirtypages, page.getParentId(), midEntry.getKey());
parent.insertEntry(midEntry);
dirtypages.put(parent.pid, parent);
updateParentPointers(tid, dirtypages, parent);
//8. Decide which page to return according to the field
boolean right = field.compare(Op.GREATER_THAN_OR_EQ, midEntry.getKey());
return right ? rightPage : page;
}
3.Delete
When deleting, there are two situations. One is that the brother page is relatively full, and you can get some elements from the brother page because you delete some tuple s or the entry is relatively empty. In this way, the brother page can not split the page so early, and you can also achieve more element ratios. This corresponds to what exercise3 needs to do; Another case is when both pages are empty. At this time, you need to consider merging the two pages into one to save space, which corresponds to what exercise4 needs to do. After the operations inserted in the front can be completed, the later routines will be found to be similar, and then the illustrations given in the handout are also easy to understand, which can help us clarify our ideas.
Exercise 3: Redistributing pages
Implement BTreeFile.stealFromLeafPage(),
BTreeFile.stealFromLeftInternalPage(),
BTreeFile.stealFromRightInternalPage().
After completing this exercise, you should be able to pass some of the unit
tests in BTreeFileDeleteTest.java (such as testStealFromLeftLeafPage and
testStealFromRightLeafPage). The system tests may take several seconds to
complete since they create a large B+ tree in order to fully test the system.
exercise3 is the reallocation of page elements. There are differences between the internal page entry and the leaf page tuple. If you reallocate a tuple, the parent needs to contain the tuple value, but you don't need to reallocate the entry, because the real data is in the leaf page, which is only used as an index. Of course, you can add it, But it will be more convenient to do so, at least as shown in the figure.
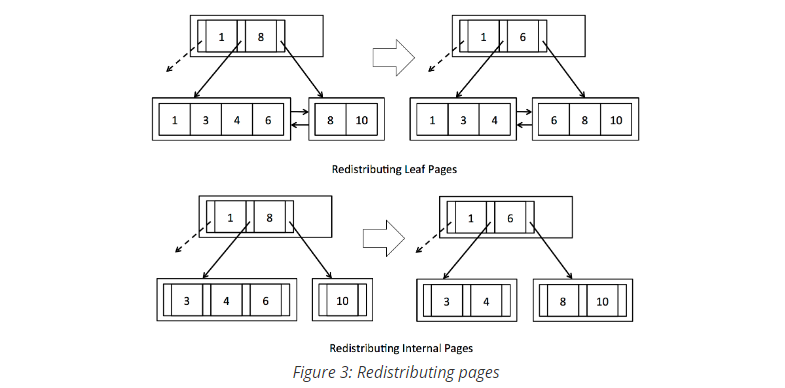
For reallocation, two strategies can be considered: the first is to add up the total number of tuples of two pages and then average them. The second is to leave 1 / 2 of the total capacity of one page and allocate the rest to empty pages. Here I use the former; Just follow the diagram in the implementation process, and then pay attention to some details.
Steel of leaf page:
public void stealFromLeafPage(BTreeLeafPage page, BTreeLeafPage sibling,
BTreeInternalPage parent, BTreeEntry entry, boolean isRightSibling) throws DbException {
// some code goes here
//
// Move some of the tuples from the sibling to the page so
// that the tuples are evenly distributed. Be sure to update
// the corresponding parent entry.
int curTuples = page.getNumTuples();
int siblingTuples = sibling.getNumTuples();
int targetTuples = curTuples + siblingTuples >> 1;
if (isRightSibling) {
//From right brother Steele
Iterator<Tuple> it = sibling.iterator();
while (it.hasNext() && curTuples < targetTuples) {
Tuple t = it.next();
//Here, delete first and then insert, because the recorded pid will be changed during the insert process. When the recorded pid does not match the pid of the current page, an error will be reported
sibling.deleteTuple(t);
page.insertTuple(t);
curTuples ++;
}
Tuple mid = sibling.iterator().next();
entry.setKey(mid.getField(parent.keyField));
parent.updateEntry(entry);
return;
}
//From left brother Steele
Iterator<Tuple> it = sibling.reverseIterator();
while (curTuples < targetTuples) {
Tuple t = it.next();
sibling.deleteTuple(t);
page.insertTuple(t);
curTuples ++;
}
Tuple mid = page.iterator().next();
entry.setKey(mid.getField(parent.keyField));
parent.updateEntry(entry);
}
Steel on the internal page: there is a hole here. The entry mentioned earlier is squeezed up. When the steel is started, it should first update the pointer of the parent. It's good to pay attention here.
public void stealFromLeftInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage page, BTreeInternalPage leftSibling, BTreeInternalPage parent,
BTreeEntry parentEntry) throws DbException, TransactionAbortedException {
// some code goes here
// Move some of the entries from the left sibling to the page so
// that the entries are evenly distributed. Be sure to update
// the corresponding parent entry. Be sure to update the parent
// pointers of all children in the entries that were moved.
int curEntries = page.getNumEntries();
int leftSiblingNumEntries = leftSibling.getNumEntries();
int targetEntries = curEntries + leftSiblingNumEntries >> 1;
Iterator<BTreeEntry> it = leftSibling.reverseIterator();
//First handle the penultimate node of parentEntry and leftSibling, and pay attention to the update of left and right child pointers
BTreeEntry right = page.iterator().next();
BTreeEntry left = it.next();
leftSibling.deleteKeyAndRightChild(left);
BTreeEntry entry = new BTreeEntry(parentEntry.getKey(), left.getRightChild(), right.getLeftChild());
page.insertEntry(entry);
page.insertEntry(left);
curEntries += 2;
while (it.hasNext() && curEntries < targetEntries) {
BTreeEntry e = it.next();
//Delete before insert
leftSibling.deleteKeyAndRightChild(e);
page.insertEntry(e);
curEntries ++;
}
BTreeEntry e = it.next();
leftSibling.deleteKeyAndRightChild(e);
parentEntry.setKey(e.getKey());
parent.updateEntry(parentEntry);
updateParentPointers(tid, dirtypages, page);
}
public void stealFromRightInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage page, BTreeInternalPage rightSibling, BTreeInternalPage parent,
BTreeEntry parentEntry) throws DbException, TransactionAbortedException {
// some code goes here
// Move some of the entries from the right sibling to the page so
// that the entries are evenly distributed. Be sure to update
// the corresponding parent entry. Be sure to update the parent
// pointers of all children in the entries that were moved.
int curEntries = page.getNumEntries();
int rightSiblingNumEntries = rightSibling.getNumEntries();
int targetEntries = curEntries + rightSiblingNumEntries >> 1;
Iterator<BTreeEntry> it = rightSibling.iterator();
BTreeEntry right = it.next();
rightSibling.deleteKeyAndLeftChild(right);
BTreeEntry left = page.reverseIterator().next();
BTreeEntry entry = new BTreeEntry(parentEntry.getKey(), left.getRightChild(), right.getLeftChild());
//Note that you need to insert entry first and then right. If you insert right first, the recordId will be updated
page.insertEntry(entry);
page.insertEntry(right);
curEntries += 2;
while (it.hasNext() && curEntries < targetEntries) {
BTreeEntry e = it.next();
rightSibling.deleteKeyAndRightChild(e);
page.insertEntry(e);
curEntries ++;
}
BTreeEntry next = it.next();
rightSibling.deleteKeyAndRightChild(next);
parentEntry.setKey(next.getKey());
parent.updateEntry(parentEntry);
updateParentPointers(tid, dirtypages, page);
}
After this, there is only the code for the last part of the experiment, that is, the combination of two pages.
Exercise 4: Merging pages
Implement BTreeFile.mergeLeafPages() and BTreeFile.mergeInternalPages().
Now you should be able to pass all unit tests in BTreeFileDeleteTest.java
and the system tests in systemtest/BTreeFileDeleteTest.java.
The merge page also needs to pay attention to the pointer update. The idea is relatively clear. Go directly to the code:
public void mergeLeafPages(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeLeafPage leftPage, BTreeLeafPage rightPage, BTreeInternalPage parent, BTreeEntry parentEntry)
throws DbException, IOException, TransactionAbortedException {
Iterator<Tuple> it = rightPage.iterator();
while (it.hasNext()) {
Tuple t = it.next();
rightPage.deleteTuple(t);
leftPage.insertTuple(t);
}
BTreePageId rrId = rightPage.getRightSiblingId();
if (rrId != null) {
BTreeLeafPage rr = (BTreeLeafPage)getPage(tid, dirtypages, rrId, Permissions.READ_WRITE);
rr.setLeftSiblingId(leftPage.pid);
leftPage.setRightSiblingId(rrId);
} else {
leftPage.setRightSiblingId(null);
}
setEmptyPage(tid, dirtypages, rightPage.pid.getPageNumber());
deleteParentEntry(tid, dirtypages, leftPage, parent, parentEntry);
}
public void mergeInternalPages(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage leftPage, BTreeInternalPage rightPage, BTreeInternalPage parent, BTreeEntry parentEntry)
throws DbException, IOException, TransactionAbortedException {
//First copy the key value of parent entry, set the pointer, and insert it into the left page
BTreeEntry lastLeftEntry = leftPage.reverseIterator().next();
BTreeEntry firstRightEntry = rightPage.iterator().next();
BTreeEntry entry = new BTreeEntry(parentEntry.getKey(), lastLeftEntry.getRightChild(), firstRightEntry.getLeftChild());
leftPage.insertEntry(entry);
//Start moving the entry on the right to the left
Iterator<BTreeEntry> it = rightPage.iterator();
while (it.hasNext()) {
BTreeEntry e = it.next();
rightPage.deleteKeyAndLeftChild(e);
leftPage.insertEntry(e);
}
//Update the pointer, set an empty page, and delete the parent entry
updateParentPointers(tid, dirtypages, leftPage);
setEmptyPage(tid, dirtypages, rightPage.pid.getPageNumber());
deleteParentEntry(tid, dirtypages, leftPage, parent, parentEntry);
}
3, Experimental summary
Lab5 because there are a lot of experimental classes in school recently, and I recently began to review the operating system and learn Redis. I feel that I have done it intermittently for a long time. It would be better to ensure that there is a continuous period of time to adjust the code as much as possible. The overall difficulty of lab5 is similar to that of lab4, but it will be very difficult at the beginning, especially when it comes to insert. It is mainly to clarify the calling relationship, when the pointer needs to be updated and how to update, as if it is the title of the linked list hhh (many places are still very similar to the linked list). The last experiment will be completed in the next week. I hope it will be completed smoothly.
Test time: 2021.10.28-2021.11.06
Writing time of experiment report: 2021.11.07-2021.11.08
htPage.deleteKeyAndLeftChild(e);
leftPage.insertEntry(e);
}
//Update the pointer, set an empty page, and delete the parent entry updateParentPointers(tid, dirtypages, leftPage); setEmptyPage(tid, dirtypages, rightPage.pid.getPageNumber()); deleteParentEntry(tid, dirtypages, leftPage, parent, parentEntry); }
# 3, Experimental summary lab5 Because there are more experimental classes in school recently, I also began to review the operating system and learning recently Redis,I think it's been done intermittently for a long time. It's better to ensure that there is a continuous period of time to adjust the code as much as possible. lab5 The overall difficulty feels like lab4 Almost. It's very difficult at first, especially when you arrive insert That part of the difficulty began to improve, mainly to clarify the call relationship, when the pointer needs to be updated and how to update, as if it was a linked list hhh(Many places are still very similar to linked lists). The last experiment will be completed in the next week. I hope it will be completed smoothly. Experiment time: 2021.10.28-2021.11.06 Experimental report writing time: 2021.11.07-2021.11.08