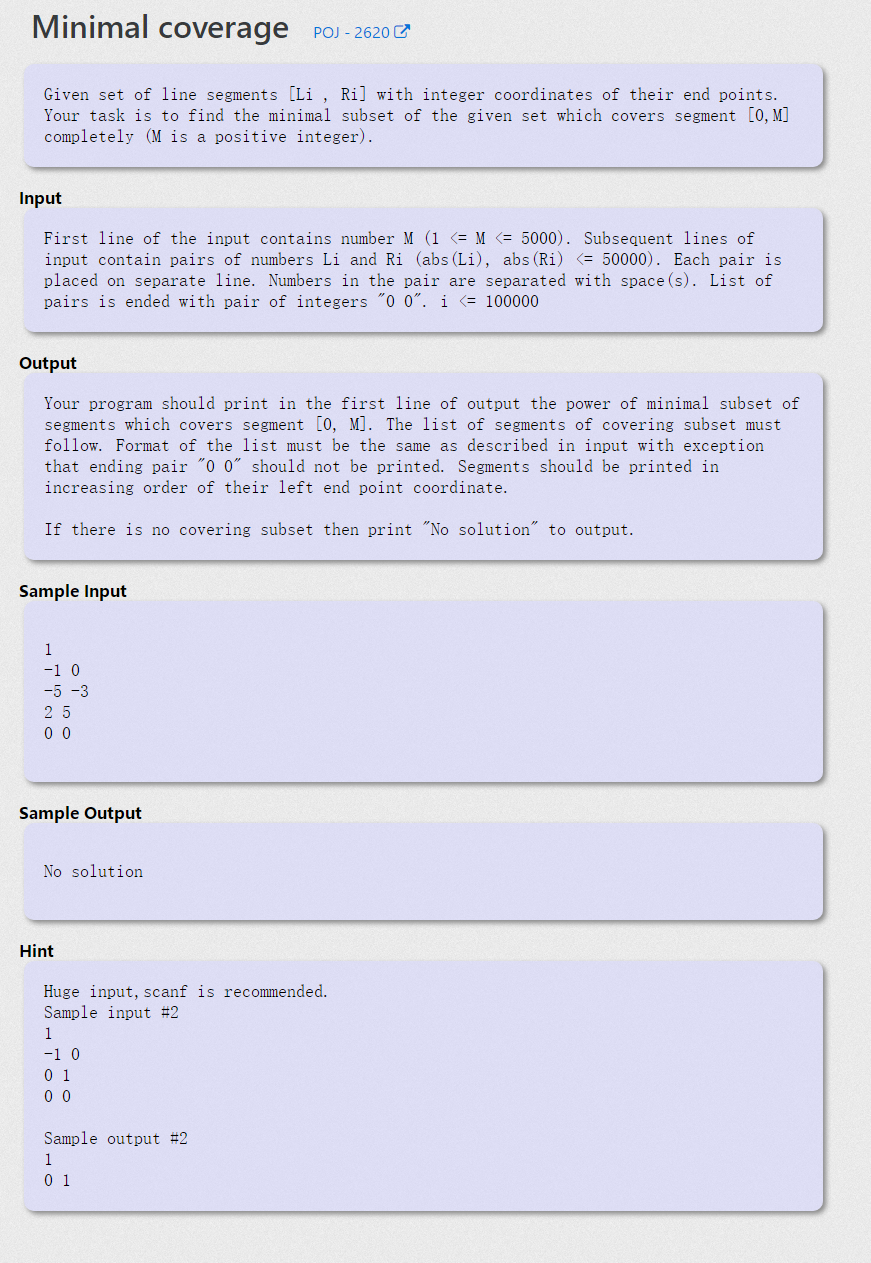
Main idea: first determine an M, then input the coordinates of the left and right ends of multiple groups of line segments, and then let you find out that in the given line segment, you can

The minimum number of lines needed to completely cover the [0, M] area, and output the left and right endpoint coordinates of these lines.

Thought analysis:

If the starting point of the interval of △ line segment is 0, then find out the most suitable interval whose starting point is less than 0.

Because you need as few intervals as possible, choose a larger interval at the right end, which contains a larger segment.

If the solution is found in all intervals and the right endpoint is less than M, then the right endpoint of the interval found is set as the starting point of the new segment interval.

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <cstring>
 4 #include <cmath>
 5 #include <algorithm>
 6 
 7 
 8 using namespace std;
 9 
10 struct node
11 {
12     int L, R;
13 }a[100010], b[100010];
14 
15 bool cmp(node a, node b)
16 {
17     return a.R > b.R;
18 }
19 
20 int main() 
21 {
22     int M;
23     while(scanf("%d", &M) != EOF)
24     {
25         int Index = 0;
26         while(1)
27         {
28             scanf("%d%d", &a[Index].L, &a[Index].R);
29             if(a[Index].L == 0 && a[Index].R == 0)
30                 break;
31             ++Index;
32         }
33         
34         sort(a, a+Index, cmp);
35         
36         int border = 0;        // Starting boundary point is 0 
37         int cnt = 0;
38         while(border < M)
39         {
40             int i = 0;
41             for(; i < Index; ++i)
42             {
43                 // a[i].R >= border Submission will Runtime error 
44                 if(a[i].L <= border && a[i].R > border)
45                 {
46                     b[cnt] = a[i];
47                     cnt++;
48                     border = a[i].R;    // Update boundary points 
49                     break;
50                 }
51             }
52             if(i == Index)
53                 break;
54         }
55         
56         
57         if(border < M)
58             cout << "No solution" << endl;
59         else
60         {
61             cout << cnt << endl;
62             for(int i = 0; i < cnt; ++i)
63                 cout << b[i].L << " " << b[i].R << endl;
64         }
65     }
66             
67     return 0;
68 }