subject

Topic Description
Input two monotonically increasing linked lists, output two combined linked lists, of course, we need to synthesize the linked list to meet the monotonic rule.
Corresponding to LeetCode21.

Thoughts on Problem Solving

Violent Solution:

1. Create a new linked list;
2. Determine the size of the two linked lists in turn, and choose a small build until the end.

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # Returns the merged list
    def Merge(self, pHead1, pHead2):
        # write code here
        if pHead1 is None and pHead2 is None:
            return None
        if pHead1 is None:
            return pHead2
        if pHead2 is None:
            return pHead1
        root = ListNode(0)
        first=root
        while pHead1 and  pHead2:
            val1=pHead1.val
            val2=pHead2.val
            if val1<=val2:
                root.next=ListNode(val1)
                pHead1=pHead1.next
            else:
                root.next=ListNode(val2)
                pHead2=pHead2.next
            root=root.next
        if pHead1:
            root.next=pHead1
        if pHead2:
            root.next=pHead2
        return first.next

Recursive approach

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # Returns the merged list
    def Merge(self, pHead1, pHead2):
        # write code here
        if pHead1 is None and pHead2 is None:
            return None
        if pHead1 is None:
            return pHead2
        if pHead2 is None:
            return pHead1
        if pHead1.val<=pHead2.val:
            pHead1.next = self.Merge(pHead1.next, pHead2)
            return pHead1
        else:
            pHead2.next = self.Merge(pHead1, pHead2.next)
            return pHead2
        

LeetCode 23 also has an upgraded version that combines K sorted linked lists.

Violent Solution:

1. Take out all values;
2. Sorting;
3. Create a new list.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        arr=[]
        for i in lists:
            while i:
                arr.append(i.val)
                i=i.next
        root=ListNode(0)
        first=root
        for i in sorted(arr):
            root.next=ListNode(i)
            root = root.next
        return first.next

Complexity analysis

Time complexity: O (N log N), where N is the total number of nodes.

1. It takes O(N) time to traverse all values.
2. A stable sorting algorithm takes O(NlogN) time.
3. It takes O(N) time to traverse and create a new ordered list at the same time.

Spatial complexity: O(N).

1. Sorting costs O(N)O(N) space (depending on the algorithm you choose).
2. Creating a new list costs O(N)O(N) space.

Merge two linked lists one by one

1. Determine if there is more than one linked list; if not, return.
2. Merge two linked lists one by one.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def Merge(self, pHead1, pHead2):
        # write code her
        root = ListNode(0)
        first=root
        while pHead1 and  pHead2:
            val1=pHead1.val
            val2=pHead2.val
            if val1<=val2:
                root.next=ListNode(val1)
                pHead1=pHead1.next
            else:
                root.next=ListNode(val2)
                pHead2=pHead2.next
            root=root.next
        if pHead1:
            root.next=pHead1
        if pHead2:
            root.next=pHead2
        return first.next
        
        
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if len(lists)==0:
            return None
        if len(lists)==1:
            return lists[0]
        res = self.Merge(lists[0],lists[1])
        for i in range(2,len(lists)):
            res = self.Merge(res,lists[i])
        return res
        
        

Complexity analysis

Time complexity: O(kN), where k is the number of linked lists.

1. We can merge two ordered lists in O(n) time, where n is the total length of the two lists.
2. Add up all the time required for the merging process and we can get: O(kN)

Spatial complexity: O(1)

1. We can merge two ordered lists in O(1) space.

But the python implementation timed out

Divided approach

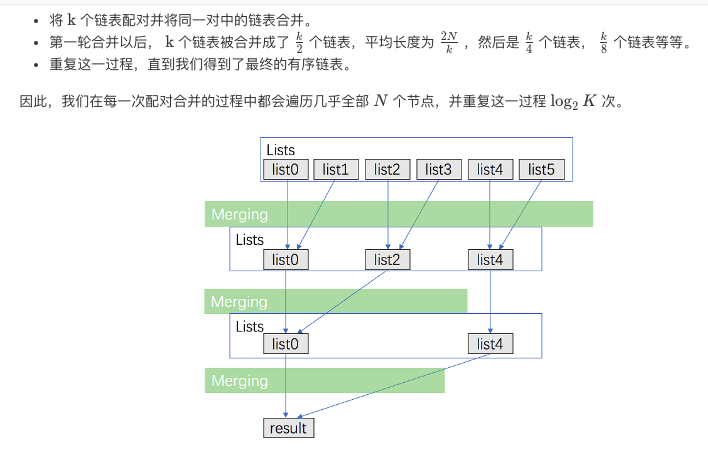
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def Merge(self, pHead1, pHead2):
        # write code here
        if pHead1 is None and pHead2 is None:
            return None
        elif pHead1 is None:
            return pHead2
        elif pHead2 is None:
            return pHead1
        elif pHead1.val<=pHead2.val:
            pHead1.next = self.Merge(pHead1.next, pHead2)
            return pHead1
        else:
            pHead2.next = self.Merge(pHead1, pHead2.next)
            return pHead2
        
        
        
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if len(lists)==0:
            return None
        if len(lists)==1:
            return lists[0]
        amount = len(lists)
        interval = 1
        while interval < amount:
            for i in range(0, amount - interval, interval * 2):
                lists[i] = self.Merge(lists[i], lists[i + interval])
            interval *= 2
        return lists[0] if amount > 0 else lists