1. Merge Sort

Recursive sorting uses recursive and divide-and-conquer techniques to divide data series into smaller and smaller semi-sub-tables, sort the semi-sub-tables, and finally merge the sorted semi-sub-tables into larger and larger ordered sequences by recursive methods.

The principle of merge sort algorithm:

For a given set of records (assuming there are n records in total), each two adjacent subsequences of 1 length are merged to get n/2 (rounding up) ordered subsequences of 2 or 1 length, then merge them into two and repeat the process until an order is obtained.Sequence.

Therefore, the key to merge and sort is two steps: the first step is to divide the semi-sub-tables; the second step is to merge the semi-sub-tables.Taking the array {49,38,65,97,76,13,27} as an example, the specific steps for merging and sorting are as follows:

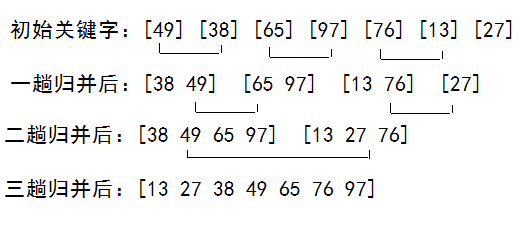
An example of the program is as follows:

public class SortMerge {

    public static void Merge(int[] array, int p, int q, int r) {
        int i,j,k,n1,n2;
        n1 = q - p + 1;
        n2 = r-q;
        int[] L = new int[n1];
        int[] R = new int[n2];
        for(i = 0, k = p; i < n1; i++, k++)
            L[i] = array[k];
        for(i = 0, k = q + 1; i < n2; i++, k++)
            R[i] = array[k];
        for(k = p, i = 0, j = 0; i < n1 && j < n2; k++) {
            if(L[i] < R[j]) {
                array[k] = L[i];
                i++;
            }
            else {
                array[k] = R[j];
                j++;
            }
        }
        if(i < n1) {
            for(j = i; j < n1; j++, k++)
                array[k] = L[j];
        }
        if(j < n2) {
            for(i = j; i < n2; i++, k++)
                array[k] = R[i];
        }
    }
    public static void MergeSort(int[] array, int p, int r) {
        if(p < r) {
            int q = (p + r)/2;
            MergeSort(array, p, q);
            MergeSort(array, q+1, r);
            Merge(array, p, q, r);
        }
    }
    public static void main(String[] args) {
        int i = 0;
        int a[] = {5,4,9,8,7,6,0,1,3,2};
        int len = a.length;
        MergeSort(a, 0, len-1);
        for(i = 0; i < len; i++)
            System.out.print(a[i] + " ");
    }
}

The process of two-way merge sort requires a logn trip.Each pass is to merge two ordered subsequences, and each pair of ordered subsequences merges, the number of records compared equals the number of records moved, and the number of records moved equals the number of records in the file n, that is, the time complexity of each merge is O(n).Therefore, the time complexity of the two-way merge sort is O(nlogn).

2. Quick Sort

Quick sorting is a very efficient sorting algorithm that uses the idea of "divide and conquer", splitting large into smaller and small into smaller.

The principle is as follows:For a given record of a word, the original sequence is divided into two parts after one-time sorting, in which all the records in the former part are smaller than all the records in the latter part, and then the records in the former and the latter parts are sorted quickly again, recursively, so that all the records in the sequence are ordered..

Specifically, the algorithm steps are as follows:
1) Decomposition.The sequence array [m...N] into two non-Confuse sequences array [m...K] and array[k+1...N], make array[m...The value of any element in k] is not greater than array[k+1...Value of any element in n].

2) Recursive solution.array[m...K] and array[k+1...n] Sort.

3) Consolidation.Since the sorting of the two decomposed subsequences is in place, it is done in array[m...K] and array[k+1...No calculation array [m...n] is already in order.

Taking the array {49,38,65,97,76,13,27,49} as an example, the entire sorting process is as follows:

An example of the program is as follows:

public class SortQuick {
    public static void sort(int[] array, int low, int high) {
        int i, j;
        int index;
        if(low >= high)
            return;
        i = low;
        j = high;
        index = array[i];
        while(i < j) {
            while(i < j && array[j] >= index)
                j--;
            if(i < j)
                array[i++] = array[j];
            while(i < j && array[i] < index)
                i++;
            if(i < j)
                array[j--] = array[i];
        }
        array[i] = index;
        sort(array, low, i-1);
        sort(array, i+1, high);
    }
    public static void quickSort(int[] array) {
        sort(array,0,array.length-1);
    }
    public static void main(String[] args) {
        int i = 0;
        int[] a= {49,38,65,97,76,13,27,49};
        quickSort(a);
        for(i = 0; i < a.length; i++) {
            System.out.print(a[i] + " ");
        }
    }
} /* Output:
13 27 38 49 49 65 76 97 
*///~

When the original sequence is ordered wholly or locally, the performance of the quick sort degrades, and then the quick sort degrades to bubble sort.