In the last section, we learned bubble sorting and Hill sorting. In this section, we continue to learn merge sorting and fast sorting.

Merge sorting: merge two or more ordered sequences into a new ordered sequence. as follows

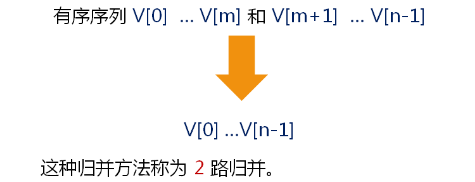
Since there are two ways to merge, there will be many ways to merge. Three ordered sequences are merged into a new ordered sequence, which is called three-way merge; N ordered sequences are merged into a new ordered sequence, which is called N-way merge; and many ordered sequences are merged into a new ordered sequence, which is called multi-way merge.

Let's take a look at the 2-way merge example, as shown in the following figure

Let's see how it works, as follows

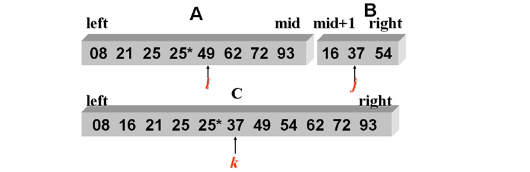
It compares two sequences one by one by comparing their sizes. Let's take a look at the implementation of merge sort. The source code is as follows.

#ifndef SORT_H
#define SORT_H

#include "Object.h"

namespace DTLib
{

class Sort : public Object
{
private:
    Sort();
    Sort(const Sort&);
    Sort& operator= (const Sort&);

    template <typename T>
    static void Swap(T& a, T& b)
    {
        T c(a);
        a = b;
        b = c;
    }

    template < typename T >
    static void Merge(T src[], T helper[], int begin, int mid, int end, bool min2max)
    {
        int i = begin;
        int j = mid + 1;
        int k = begin;

        while( (i <= mid) && (j <= end) )
        {
            if( min2max ? (src[i] < src[j]) : (src[i] > src[j]) )
            {
                helper[k++] = src[i++];
            }
            else
            {
                helper[k++] = src[j++];
            }
        }

        while( i <= mid )
        {
            helper[k++] = src[i++];
        }

        while( j <= end )
        {
            helper[k++] = src[j++];
        }

        for(i=begin; i<=end; i++)
        {
            src[i] = helper[i];
        }
    }

    template < typename T >
    static void Merge(T src[], T helper[], int begin, int end, bool min2max)
    {
        if( begin < end )
        {
            int mid = (begin + end) / 2;

            Merge(src, helper, begin, mid, min2max);
            Merge(src, helper, mid+1, end, min2max);
            Merge(src, helper, begin, mid, end, min2max);
        }
    }

public:
    template < typename T >
    static void Merge(T array[], int len, bool min2max = true)
    {
        T* helper = new T[len];

        if( helper != NULL )
        {
            Merge(array, helper, 0, len-1, min2max);
        }

        delete[] helper;
    }
};

}

#endif // SORT_H

The test code is as follows

#include <iostream>
#include "Sort.h"

using namespace std;
using namespace DTLib;

int main()
{
    int array[] = {9, 3, 2, 4, 1, 5, 7, 6, 9, 8};

    Sort::Merge(array, 10);

    for(int i=0; i<10; i++)
    {
        cout << array[i] << endl;
    }
}

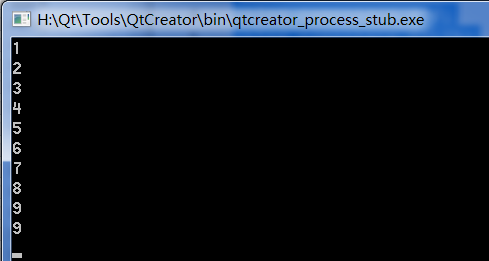
Let's take a look at the results.

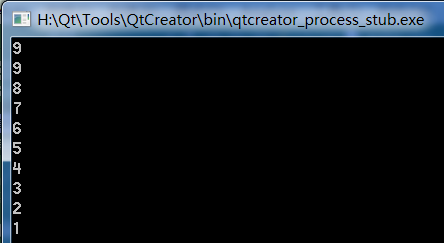
We change the above parameter to false, and let it sort from large to small. The results are shown in the following figure

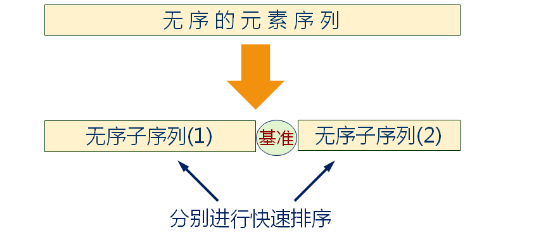
2. Quick sorting: The whole sequence is divided into left and right subsequences by selecting a data element in the sequence as a benchmark. All elements in the left subsequence are less than or equal to the reference elements, while all elements in the right subsequence are larger than the reference elements, and the reference elements are in the middle of the two subsequences. The two subsequences are divided separately, and all the data elements are in the corresponding position.

The quick sort example is as follows

Let's see how this is achieved, as follows

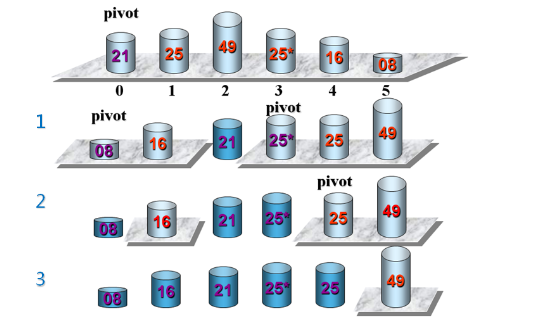
We see that a data element is selected as the base element, larger than it on the right, smaller than it on the left. Once again, select an element in the left subsequence as the reference element, and so on. Let's look at the implementation of the specific source code, as follows

#ifndef SORT_H
#define SORT_H

#include "Object.h"

namespace DTLib
{

class Sort : public Object
{
private:
    Sort();
    Sort(const Sort&);
    Sort& operator= (const Sort&);

    template <typename T>
    static void Swap(T& a, T& b)
    {
        T c(a);
        a = b;
        b = c;
    }

    template < typename T >
    static int Partition(T array[], int begin, int end, bool min2max)
    {
        T pv = array[begin];

        while( begin < end )
        {
            while( (begin < end) && (min2max ? (array[end] > pv) : (array[end] < pv)) )
            {
                end--;
            }

            Swap(array[begin], array[end]);

            while( (begin < end) && (min2max ? (array[begin] <= pv) : (array[begin] >= pv)) )
            {
                begin++;
            }

            Swap(array[begin], array[end]);
        }

        array[begin] = pv;

        return begin;
    }

    template < typename T >
    static void Quick(T array[], int begin, int end, bool min2max)
    {
        if( begin < end )
        {
            int pivot = Partition(array, begin, end, min2max);

            Quick(array, begin, pivot-1, min2max);
            Quick(array, pivot+1, end, min2max);
        }
    }

public:
    template < typename T >
    static void Quick(T array[], int len, bool min2max = true)
    {
        Quick(array, 0, len-1, min2max);
    }
};

}

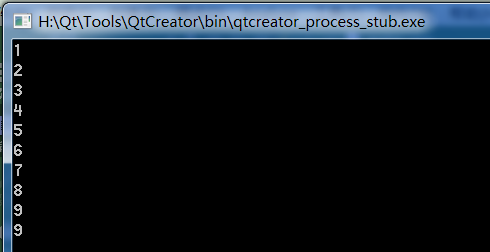
#endif // SORT_H

The test code is to replace the merge sort above with the quick sort. Let's first look at the case of sorting from small to large without parameters. By default, the results are as follows

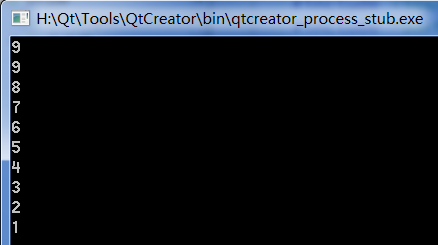
Let's look at the permutation from large to small with parameter false, and the results are as follows

Then the function has been implemented. Through today's study of merge sorting and quick sorting, we can conclude as follows: 1. Merge sorting needs additional auxiliary space to complete, and its spatial complexity is O(n); 2. Merge sorting time complexity is O(n*logn), which is a stable sorting method; 3. Quick sorting divides sorting problem by recursive way; 4. Quick sorting time complexity is O(n*logn). It is an unstable sorting method.