The main idea of merge sort algorithm is to merge two ordered arrays into an ordered array. Its key point adopts the "divide and conquer idea". The "divide" is a dichotomy, which divides the unordered array into ordered arrays, and then through the "divide and conquer"   Merge two ordered arrays into one ordered array. The time complexity is O(nlogn), and the space complexity is a constant temporary variable of O(n). It is a stable sorting algorithm.

The main implementation ideas of merging and sorting are as follows:

Using the idea of "divide and conquer", the whole unordered array is first recursive on the left and then recursive on the right. Similar to the binary tree preorder traversal method, the array is divided into ordered arrays; Then, through the "rule", the ordered arrays are combined into an ordered array through the merge method;

1. "Min" vector < int > merge (vector < int > & num, int start, int end); Dichotomy starts at the start and end positions.

vector<int> Sorts::merge(vector<int>& nums, int start, int end)
{
    if (start == end) //Recursion termination condition: if the start subscript is equal to the end subscript, recursion is terminated
        return { nums[start] }; // Returns the first element on the left
    int middle = (start + end) / 2; // Divide and conquer, using dichotomy, take the middle subscript and start left and right recursion until an element begins to return
    auto left = merge(nums, start, middle); // First recurse the left part, exit the layer, and then recurse to the right until an element
    print(left);
    auto right = merge(nums, middle + 1, end); // Recursively take the ordered array from the left to the right
    return merge(left, right); // Merge two ordered arrays, and then continue to fall back to the left or right of the previous layer until the whole recursion ends and returns
}

Always traverse the left part of the data, and then return to the upper layer to traverse the right part of the data, so that each time the left and right parts of the sub get one by one or a combined ordered data group.

That is, as shown in Figure 1 below, the value on the left after traversal is printed every time. It can be analyzed that this recursion is similar to the preorder traversal in a binary tree. Each time, the left element is traversed first, back to the upper layer, and then the innermost element on the right. The print data in Figure 2 further confirms that the left edge is traversed first, and then the right order is traversed.

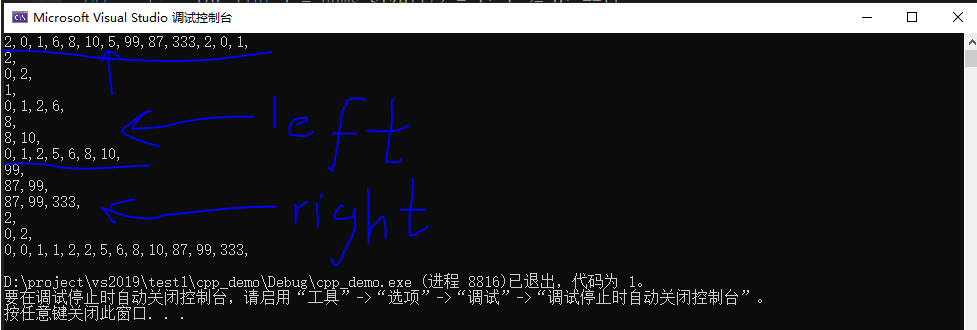Figure 1   Print the left value after merging, sorting and traversal

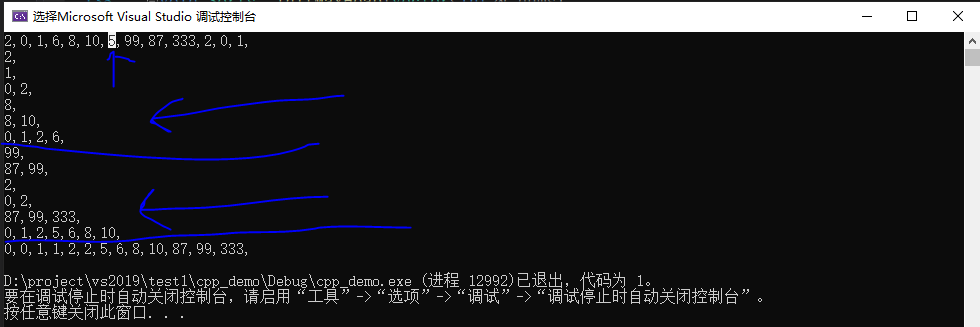Figure 2   Print the right value after merging, sorting and traversal

  2. In step 1, the unnecessary array is divided into one or one block ordered array. At this time, the two ordered arrays need to be combined into an ordered array vector < int > merge (vector < int > & nums1, vector < int > & nums2);

The key of merging is to traverse two arrays with two walking subscripts, and put one of the smaller elements into the newly created array; When one of the arrays is traversed, the remaining arrays are placed behind the new array to complete the sorting; The following code is shown:

vector<int> Sorts::merge(vector<int>& nums1, vector<int>& nums2)
{
    int i1{ 0 }, i2{ 0 };
    vector<int> mergeArr(nums1.size() + nums2.size(), 0);
    while (i1 < nums1.size() && i2 < nums2.size()) // Traverse two arrays with two subscripts respectively, and put the smaller elements into the new array until one of the arrays is traversed
    {
        //mergeArr[i1 + i2] = nums1[i1] <= nums2[i2] ?  nums1[i1++] : nums2[i2++];  This line is OK under linux, but there is an error in the msvc compiler section
        if (nums1[i1] <= nums2[i2]) // Take the smaller element and put it into the new array
        {
            mergeArr[i1 + i2] = nums1[i1]; // 
            ++i1; // msvc + + seems to be different from the implementation of gcc compiler. Putting it in the array here will cause a segment error
        }
        else
        {
            mergeArr[i1 + i2] = nums2[i2];
            ++i2;
        }
    }
    while (i1 < nums1.size()) // Put the remaining array after the new array
    {
        mergeArr[i1 + i2] = nums1[i1];
        ++i1;
    }
    while (i2 < nums2.size()) // Put the remaining array after the new array
    {
        mergeArr[i1 + i2] = nums2[i2];
        ++i2;
    }
    return mergeArr;
}

3. The following is a complete example code:

Sorts.h

#pragma once

#include <iostream>
#include <vector>

using namespace std;

struct Sorts {    
    void merge(vector<int>& nums);
    
    void print(vector<int>& nums);

private:    
    vector<int> merge(vector<int>& nums, int start, int end);
    vector<int> merge(vector<int>& nums1, vector<int>& nums2);
};

Sorts.cpp

#include "Sorts.h"

void Sorts::merge(vector<int>& nums)
{
    if (nums.size() <= 1)
    {
        return;
    }
    auto tmpNums = merge(nums, 0, nums.size() - 1);
    nums = tmpNums;
}

void Sorts::print(vector<int>& nums)
{
    for (const auto& it : nums)
        cout << it << ",";
    cout << endl;
}

vector<int> Sorts::merge(vector<int>& nums, int start, int end)
{
    if (start == end) //Recursion termination condition: if the start subscript is equal to the end subscript, recursion is terminated
        return { nums[start] }; // Returns the first element on the left
    int middle = (start + end) / 2; // Divide and conquer, using dichotomy, take the middle subscript and start left and right recursion until an element begins to return
    auto left = merge(nums, start, middle); // First recurse the left part, exit the layer, and then recurse to the right until an element
    auto right = merge(nums, middle + 1, end); // Recursively take the ordered array from the left to the right    
    return merge(left, right); // Merge two ordered arrays, and then continue to fall back to the left or right of the previous layer until the whole recursion ends and returns
}

vector<int> Sorts::merge(vector<int>& nums1, vector<int>& nums2)
{
    int i1{ 0 }, i2{ 0 };
    vector<int> mergeArr(nums1.size() + nums2.size(), 0);
    while (i1 < nums1.size() && i2 < nums2.size()) // Traverse two arrays with two subscripts respectively, and put the smaller elements into the new array until one of the arrays is traversed
    {
        //mergeArr[i1 + i2] = nums1[i1] <= nums2[i2] ?  nums1[i1++] : nums2[i2++];  This line is OK under linux, but there is an error in the msvc compiler section
        if (nums1[i1] <= nums2[i2]) // Take the smaller element and put it into the new array
        {
            mergeArr[i1 + i2] = nums1[i1]; // 
            ++i1; // msvc + + seems to be different from the implementation of gcc compiler. Putting it in the array here will cause a segment error
        }
        else
        {
            mergeArr[i1 + i2] = nums2[i2];
            ++i2;
        }
    }
    while (i1 < nums1.size()) // Put the remaining array after the new array
    {
        mergeArr[i1 + i2] = nums1[i1];
        ++i1;
    }
    while (i2 < nums2.size()) // Put the remaining array after the new array
    {
        mergeArr[i1 + i2] = nums2[i2];
        ++i2;
    }
    return mergeArr;
}

main.cpp

Output results: