Chapter 3 string
3.1 creation of string array
1. Direct input method
2. Using ASCII code
3. Using functions
[example 3-1] direct input method
>> a = 'hello' a = hello >> b = '''Hello''' b = 'Hello' >> c = [a,'',b,'.']#String array (an array, which is a string) c = hello'Hello'.
Be careful:
1. When the string text contains single quotation marks, each single quotation mark symbol needs to use two consecutive single quotation mark characters (different from double quotation marks in python)
2. String is a special ASCII numeric array, but it shows the character form.
[example 3-2] using ASCII code
>> b = 'Hello'; >> ASCIIb = double(b); >> c = char(ASCIIb); >> b b = //Hello >> ASCIIb ASCIIb = 20320 22909 >> c c = //Hello
[example 3-3] use function
Correlation function: char(), str2mat(), strvcat()
Strings are arranged vertically, and it is not necessary to notice whether the length of each string variable is equal.
>> c1 = char('China Dalian','ccit') c1 = China Dalian ccit >> c2 = str2mat('China','Dalian','','ccit') c2 = China Dalian ccit >> a1 = 'auto'; >> a2 = 'film'; >> a3 = 'forest'; >> a4 = 'city'; >> b1 = strvcat(a1,a4); >> b2 = strvcat(a2,a4); >> b3 = strvcat(a3,a4); >> b1 b1 = auto city >> b2 b2 = film city >> b3 b3 = forest city
At the same time, the function that provides the concatenation string in Matlab: strcat()
[example 3-4]
>> a1 = 'auto'; >> a2 = 'city'; >> b1 = strcat(a1,a2) b1 = autocity
Note: the strcat() function will delete all spaces at the end of each string when merging strings
3.2 conversion between value and string
1. Convert value to string: int2str(), num2str(), mat2str() (integer, value, matrix)
[example 3-5]
>> A1 = int2str(eye(4)) A1 = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 >> size(A1) ans = 4 10 #The result is a character matrix with 4 lines and 10 columns, indicating that the space between numbers is also calculated, that is, the space has become a character >> A2 = num2str(rand(3)) A2 = 0.81472 0.91338 0.2785 0.90579 0.63236 0.54688 0.12699 0.09754 0.95751 >> size(A2) ans = 3 31 #In the same way as above, the original value has been changed to a string #num2str is more applicable than int2str >> A3 = mat2str(pi/2*eye(2)) A3 = [1.5707963267949 0;0 1.5707963267949]#Notice the semicolon in the middle >> size(A3) ans = 1 37
2. String conversion to numeric value: str2num(), str2double()
[example 3-6]
>> s = num2str(log(3)*eye(3)) s = 1.0986 0 0 0 1.0986 0 0 0 1.0986 >> ischar(s) #Determine whether s is a string array ans = 1 >> n = str2num(s) n = 1.0986 0 0 0 1.0986 0 0 0 1.0986 >> isnumeric(n) #Determine whether n is a numerical array ans = 1 >> isfloat(n) #Determine whether n is a floating-point value array ans = 1
3.3 string function
1.ischar(): determine whether the value in brackets is a string array
2.findstr(): used to find the location
[example 3-7]
>> S = 'Find another string in a longer string.'; >> result = findstr(S,'longer') #Find the location of 'long' result = 26 #Returns the starting position of the searched string >> result2 = findstr(S,'a') #Find the location of 'a' result2 = 6 24 #There are two a's, return two values >> result3 = findstr(S,'b') result3 = [] #There is no 'b' in S, so the return value is empty
3.upper(): convert the lowercase letters in the string in brackets to uppercase letters
4.lower(): convert the uppercase letters in the string in brackets to lowercase letters
3.4 cell array
Definition:
Cell Array, the basic structure of which is a cell, each element is a cell, which can contain any type and size of array, and the contents of each cell in the same Cell Array can be different, its dimension is unlimited, it can be one-dimensional, two-dimensional or multi-dimensional.
3.4.1 creation of cell array:
1. Using assignment statement
3. Using function cell
[example 3-8] using assignment statements (two forms)
The first is:
>> A(1,1) = {'Matlab'}; >> A(1,2) = {'7.0'}; >> A(2,1) = {'matrix'}; >> A(2,2) = {[1 2 3;4 5 6;7 8 9]}; >> A A = 'Matlab' '7.0' 'matrix' [3x3 double]
Second species:
>> A{1,1} = 'Matlab'; >> A{1,2} = '7.0'; >> A{2,1} = 'matrix'; >> A{2,2} = [1 2 3;4 5 6;7 8 9]; >> A A = 'Matlab' '7.0' 'matrix' [3x3 double]
[example 3-9] using cell array method
>> A = {'Matlab','7.0';'matrix',[1 2 3;4 5 6;7 8 9]} A = 'Matlab' '7.0' 'matrix' [3x3 double]
[example 3-10] using function cell
>> C = cell(3) C = [] [] [] [] [] [] [] [] [] >> C(1,1) = {'The Great Wall'} C = 'The Great Wall' [] [] [] [] [] [] [] [] >> C(1,2) = {'The Summer Palace'} C = 'The Great Wall' 'The Summer Palace' [] [] [] [] [] [] [] >> C(2,1) = {[1 2;2 1]} C = 'The Great Wall' 'The Summer Palace' [] [2x2 double] [] [] [] [] [] >> C(3,2) = {'celldisp'} C = 'The Great Wall' 'The Summer Palace' [] [2x2 double] [] [] [] 'celldisp' []
Supplement:
1.cell(n): establish nn cell array, cell is empty matrix; cell(m,n) or cell([m,n]): establish mn cell array, cell is empty matrix
In fact, the cell function creates an array of cells by first generating an empty array of cells, and then adding the required data to it
3.4.2 view function of cell array
Function: celldisp(),cellplot()
[example 3-11]
>> A(1,1) = {[3 2 0;6 3 9;5 5 5]}; >> A(1,2) = {1 + i}; >> A(2,1) = {'cellarray'}; >> A(2,2) = {-3:6}; >> A A = [3x3 double] [1.0000 + 1.0000i] 'cellarray' [1x10 double] >> celldisp(A) A{1,1} = 3 2 0 6 3 9 5 5 5 A{2,1} = cellarray A{1,2} = 1.0000 + 1.0000i A{2,2} = Columns 1 through 9 -3 -2 -1 0 1 2 3 4 5 Column 10 6 >>cellplot(A)
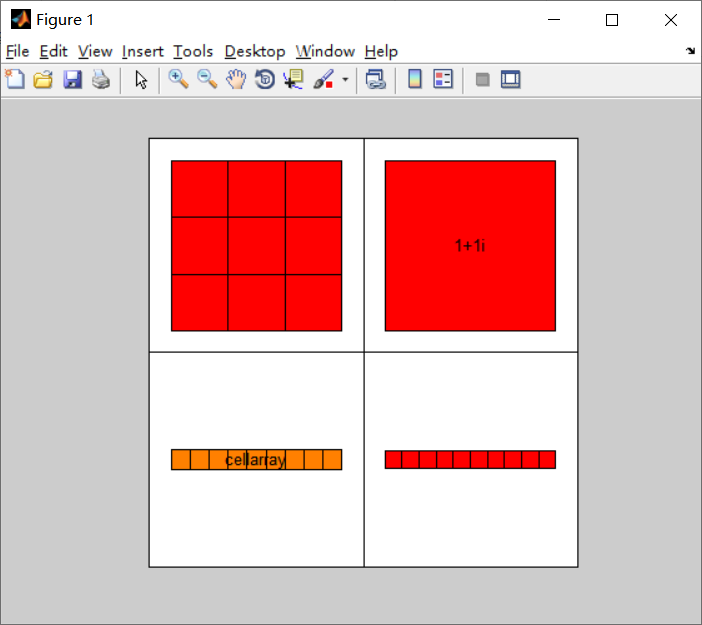
As can be seen from the above figure, the cellplot command uses a large white square to represent each cell, a small square to represent the cell content, and a color to represent the data type
Be careful:
. The difference between the two is only in parentheses or curly braces)

