Firstly, the effect map is shown.

Effect analysis

Because the ultimate goal is to achieve a painting brush under windwos, so first of all, we need to do a more detailed analysis of its effect. Considering the point of use of the brush in general, the effect details of the point and line will be analyzed.
Draw points

From left to right, click on the same coordinate twice, click on 8 times, and click on 16 times to show the effect.
When the number of points tends to be larger, there is no obvious deviation in the intensity of points, and it can be basically determined that the points should be evenly distributed in the circle.
Draw line

As shown in the figure, the line is made up of points with uniform speed and slow sliding.

Concrete realization

The general framework of the project consists of View, BasePen and two large modules. View belongs to UI level and BasePen belongs to business logic level. Next, the specific functions and details of these two modules will be introduced one by one.

View

This project bears View as PenView, does not bear business logic, is to play the role of a container. The only function in PenView is to trigger the invalidate () method.

@Override
public boolean onTouchEvent(MotionEvent event) {
    MotionEvent event1 = MotionEvent.obtain(event);
    mBasePen.onTouchEvent(event1);
    switch (event.getActionMasked()) {
        case MotionEvent.ACTION_DOWN:
        case MotionEvent.ACTION_MOVE:
            invalidate();
            break;
        case MotionEvent.ACTION_UP:
            break;
    }
    return true;
}

@Override
protected void onDraw(Canvas canvas) {
    super.onDraw(canvas);
    mBasePen.onDraw(canvas);
}

Specific business logic, such as drawing, data computing, touch point mobile Move, are all implemented by BasePen and its subclasses.
Specific business logic, such as drawing, data computing, touch point mobile Move, are all implemented by BasePen and its subclasses.
Lower coupling, representing more degrees of freedom, has less impact on existing project code (if applied to the project). In terms of performance, if View does not meet the requirements, it can be ported to SurfaceView with better performance at a lower cost.

Business logic

Business aspect, BasePen as the base class, undertakes some basic data calculation, drawing and other functions, while the specific brush effect is implemented by subclasses.
First look at what BasePen has done:
Draw

 private List<Point> mPoints;
public void onDraw(Canvas canvas) {
        if (mPoints != null && !mPoints.isEmpty()) {
            canvas.drawBitmap(mBitmap, 0, 0, null);
            drawDetail(canvas);
        }
    }   

First the brush is drawn on a Bitmap, and then the Bitmap is handed over to PenView for drawing. Point is a class that records only x and y coordinates.
DraDetail (Canvas canvas) is an abstract class that implements concrete drawing by subclasses.

The sliding trajectory is in BasePen's onTouchEvent (Motion Event 1) method. Starting with each DOWN event, all coordinate information in MOVE is recorded. Considering that the effect of spraying paint does not need to deal with the effect of pen tip, it is not considered to record UP information (if other brush effects are realized later, it will be optimized here). `

public void onTouchEvent(MotionEvent event1) {
    switch (event1.getActionMasked()) {
        case MotionEvent.ACTION_DOWN:
            clearPoints();
            handlePoints(event1);
            break;
        case MotionEvent.ACTION_MOVE:
            handlePoints(event1);
            break;
        case MotionEvent.ACTION_UP:
            break;
    }
}

  private void handlePoints(MotionEvent event1) {
        float x = event1.getX();
        float y = event1.getY();
        if (x > 0 && y > 0) {
            mPoints.add(new Point(x, y));
        }
    }  

​
private void clearPoints() {
if (mPoints == null) {
return;
}
mPoints.clear();
}

Spray painting realization

protected void drawDetail(Canvas canvas) {
        if (getPoints().isEmpty()) {
            return;
        }
        mTotalNum = Calculated from custom particle density and brush width
        drawSpray(Current up-to-date coordinate points.x, Current up-to-date coordinate points.y, mTotalNum);
    }

private void drawSpray(float x, float y, int totalNum) {
    for (int i = 0; i < totalNum; i++) {
        //The algorithm calculates random points in a circle
        float[] randomPoint = getRandomPoint(x, y, mPenW, true);
        mCanvas.drawCircle(randomPoint[0], randomPoint[1], mCricleR, mPaint);
    }
}

This is part of the pseudocode. SprayPen internally defines a paint particle density that changes the number of particles in real time according to the width of the brush. The radius of each particle is calculated by width provided by externally dependent components.
In drawDetail(... ) In this method, every MOVE and DOWN event will draw a certain number of random points in the circle at the corresponding coordinates.
When it is connected in series, the effect of spraying paint is formed. Of course, this is only preliminary completion, there are still some algorithms need to be improved. Pseudo-code is incomplete, refer to SprayPen, there are more perfect comments in the code.

Next, I will talk about some problems about spray painting algorithm.

SOME PROBLEMS OF SPRAYING ALGORITHM

There are two issues worth documenting in the implementation of the functionality.
One is the distribution of uniform random points in a circle.
Second, when the sliding speed is fast, the connection of strokes is dealt with.

How to uniformly generate random points in a circle

In order to solve this problem, three methods are tried:

x is randomly selected in the range of (-R,R), and is analytically expressed by a circle.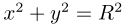
The solution is y. Then, the random value of Y in (-y,y) is taken, and the obtained point is the inner point of the circle. Similarly, x can also be calculated from y.
The java code is as follows:

float x = mRandom.nextInt(r);
float y = (float) Math.sqrt(Math.pow(r, 2) - Math.pow(x, 2));
y = mRandom.nextInt((int) y);
x = Random positive and negative pairing(x);
y = Random positive and negative pairing(y);

The final results are as follows:

When the number of samples reaches 2000, the shape can be clearly seen as shown above. In the direction of x-axis, the density of left and right ends is obviously higher than that of center random values. It can be understood that when there are a lot of data, the value of X is approximately uniformly distributed in (-r,r), and the value of y is also the same.
When the left and right ends are located, the value range of y becomes smaller and the visual effect becomes more compact. Of course, it would be more convincing to use the mathematical statistics formula of probability theory to verify, but unfortunately not.

Random angles are randomly obtained in [0,360], then the values are randomly selected in [0,r], and then sin s and cos are used to solve x and y.

The java code is as follows:

float[] ints = new float[2];
int degree = mRandom.nextInt(360);
double curR = mRandom.nextInt(r)+1;
float x = (float) (curR * Math.cos(Math.toRadians(degree)));
float y = (float) (curR * Math.sin(Math.toRadians(degree)));
x = Random positive and negative pairing(x);
y = Random positive and negative pairing(y);

The final results are as follows:

It is obvious that the density of the center is higher than that of the edge. In fact, when the angle is fixed, r is randomly selected in the range of [0, r]. When the number is larger, the coordinate points are evenly distributed.
When r is smaller, the smaller the area occupied, the more dense the particles will appear.

Random angle is obtained randomly in [0,360]. The random square root in [0,1] is multiplied by R. Then sin and cos are used to solve x and y.

The java code is as follows:

int degree = mRandom.nextInt(360);
double curR = Math.sqrt(mRandom.nextDouble()) * r;
float x = (float) (curR * Math.cos(Math.toRadians(degree)));
float y = (float) (curR * Math.sin(Math.toRadians(degree)));
x = Random positive and negative pairing(x);
y = Random positive and negative pairing(y);

The final results are as follows:

This time the visual effect is evenly achieved. This algorithm takes advantage of the characteristics of a root function, as shown in the following figure:

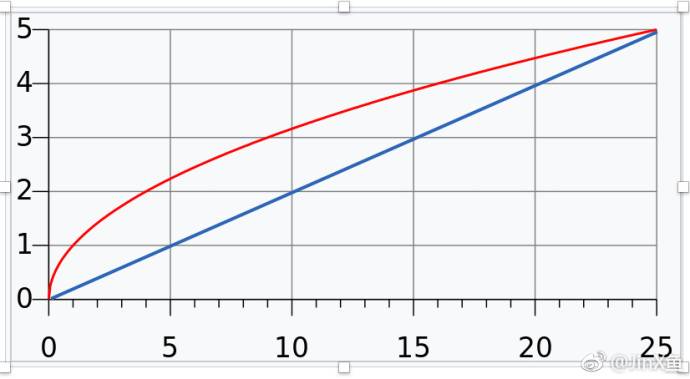
Red is the root function and blue is the linear function. Comparing the two, the value of the root function will be larger, correspondingly, more points near the edge will make the distribution of particles more balanced.

Handling the situation of "Fenbi Jishu"

When sliding at a slower speed, the strokes are still fluent and there are no obvious faults. When the speed is too fast, MOVE leaves fewer points and has large spacing. There will be brush fault phenomenon, which requires some special treatment methods.

A standard value D is set in the code, which is calculated from the values w and h held by BasePen. Generally speaking, these two values are expected to be the width of the dependent View.

Initially, the use of brush diameter calculation was also considered, but considering that the drawing straight diameter can be dynamically changed externally. Standard values are best kept independent. The more stable the data they depend on, the better. Otherwise, it will affect the balance.

Then when MOVE, when the relative distance between the current point and a point is greater than the standard value D, it will be judged that the current point is in a fast-moving state. The larger the distance, the faster the speed of movement, then the paint effect will be reduced accordingly. [Intuitively speaking, the concentration of particles is low].

In the fast-moving state, the code simulates some handwriting points between the current point and the previous point. Correspondingly, the particle density of these handwriting points is lower, and its calculation function is an anti-hump state. That is to say, the midpoint particles of continuous handwriting points are the most sparse, while the two sides are the most dense.

//When the speed is too fast
float stepDis = mPenR * 1.6f;
//Number of handwriting points
int v = (int) (getLastDis() / stepDis);
float gapX = getPoints().get(getPoints().size() - 1).x - getPoints().get(getPoints().size() - 2).x;
float gapY = getPoints().get(getPoints().size() - 1).y - getPoints().get(getPoints().size() - 2).y;
//Description of handwriting points
for (int i = 1; i <= v; i++) {
    float x = (float) (getPoints().get(getPoints().size() - 2).x + (gapX * i * stepDis / getLastDis()));
    float y = (float) (getPoints().get(getPoints().size() - 2).y + (gapY * i * stepDis / getLastDis()));
    drawSpray(x, y, (int) (mTotalNum * calculate(i, 1, v)), mRandom.nextBoolean());
            }
/**
     * (x-(min+max)/2)^2/(min-(min+max)/2)^2 is used as the density ratio function of particles.
     */
    private static float calculate(int index, int min, int max) {
        float maxProbability = 0.6f;
        float minProbability = 0.15f;
        if (max - min + 1 <= 4) {
            return maxProbability;
        }
        int mid = (max + min) / 2;
        int maxValue = (int) Math.pow(mid - min, 2);
        float ratio = (float) (Math.pow(index - mid, 2) / maxValue);
        if (ratio >= maxProbability) {
            return maxProbability;
        } else if (ratio <= minProbability) {
            return minProbability;
        } else {
            return ratio;
        }
    }

Author Zhang Yifeng
Article link https://blog.csdn.net/haizixm/article/details/80778043