Machine learning_ 1:K-nearest neighbor algorithm

Experimental background

This experiment is based on the classical k-nearest neighbor algorithm of machine learning. I will first introduce the principle of k-nearest neighbor algorithm and basic classification experiments, and then introduce how to use k-nearest neighbor algorithm for handwriting recognition.

1.k-nearest neighbor algorithm

1.1 algorithm principle

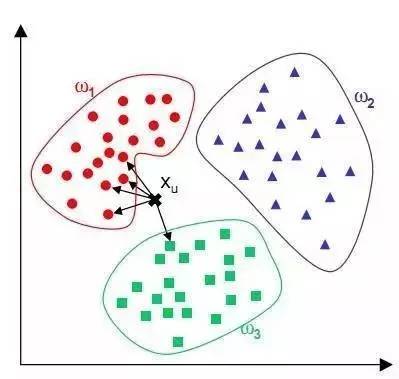
What is k-nearest neighbor algorithm is to find k nearest points according to a given point to be judged. Among the k points, which label appears the most times, the point to be judged belongs to that label. As shown in the figure, the value of K here is 5, and among the five points, there are four w1, so this judgment point belongs to w1, which is the k-nearest neighbor algorithm.
Pseudo code:
Perform the following operations for each point in the test dataset in turn:
(1) Calculate the distance between the point in the training data set and the current point;
(2) Sort by increasing distance from small to large;
(3) Select the k points with the minimum distance from the current point;
(4) Determine the occurrence frequency of the category where the k points are located (i.e. count the number of each category in the k points)
(5) The category with the highest frequency among the k points is returned as the prediction classification of the current point

1.2 algorithm analysis

The following code is k-The principle code of nearest neighbor algorithm, I will try to analyze most of the code, so that everyone reading this article can understand it

#Scientific computing package numpy
from numpy import *            
#Operator module 
import operator                 
def createDataSet():
    group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels=['A','A','B','B']
    return group,labels

#Four parameters: input vector inx (input test coordinate point), training sample set dataSet (the array group above), label vector labels (the labels above), and k is the number of nearest neighbors (k in kNN algorithm)
def classify0(inx,dataSet,labels,k):
    #Read the length of the first dimension of the matrix
    dataSetSize=dataSet.shape[0]
    #diffMat stores the difference between the input vector inx and the sample set dataSet calculated through tile
    diffMat=tile(inx,(dataSetSize,1))-dataSet
    #Square each number in the diffMat array
    sqDiffMat=diffMat**2
    #Sum these numbers
    sqDistances=sqDiffMat.sum(axis=1)
    #Root the summation result
    distances=sqDistances**0.5
    #Sort data from small to large
    sortedDistIndicies=distances.argsort()
    #Build dictionary
    classCount={}
    #Cycle k times
    for i in range(k):
        #Match labels to sort order
        voteIlabel=labels[sortedDistIndicies[i]]
        #Statistics label frequency
        classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
    #Sort again and sort in descending order according to the order of the second element
    sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
    #Returns the most frequent tag
    return sortedClassCount[0][0]

The distance calculation formula adopts the European distance formula, which is as follows:

It can be simply understood as the square sum of the difference of the corresponding coordinates and then the root sign

1.3 algorithm experiment

As shown in the figure, click the path above, enter cmd to open the command prompt, and enter it in sequence
python
import KNN (the file you named to save the k-nearest neighbor algorithm)
group,labels=KNN.createDataSet() (create group and labels)
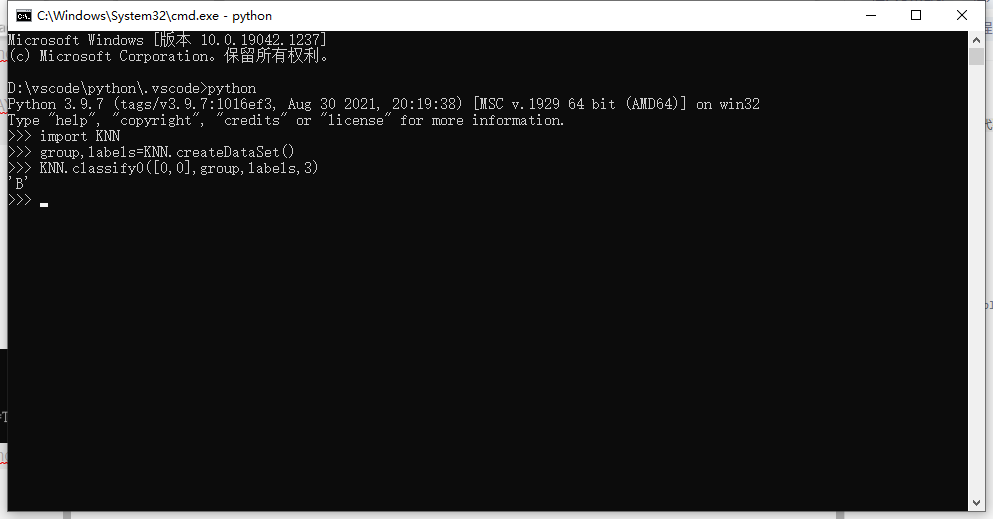
KNN.classify0([0,0],group,labels,3)
Errors may appear here

The reason is that the new version of python no longer supports iteritems. Just change it to items
The test result is shown in the figure, and the result is B (if it is not B, please pay attention to whether the code is different)

2. Handwriting recognition based on k-nearest neighbor algorithm

2.1 code analysis

#Convert the 32 * 32 image into a 1 * 1024 vector
def img2vector(filename):
    #initialization
    returnVect=zeros((1,1024))
    #Open file
    fr=open(filename)
    #Cyclic assignment
    for i in range(32):
        lineStr=fr.readline()
        for j in range(32):
            returnVect[0,32*i+j]=int(lineStr[j])
    #Return array
    return returnVect

#Handwriting recognition test set code
def handwritingClassTest():
    #Create an empty label array
    hwLabels=[]
    #Get directory content
    trainingFileList=listdir('trainingDigits')
    #Get the number of training sets
    m=len(trainingFileList)
    #initialization
    trainingMat=zeros((m,1024))
    #Cycle m times
    for i in range(m):
        #Get file name
        fileNameStr=trainingFileList[i]
        #Remove file suffix
        fileStr=fileNameStr.split('.')[0]
        #The file naming format is k_x. Like 9_ 45 (indicating that the picture is the number 9, ranking 45th in this kind of image), and obtain the category
        classNumStr=int(fileStr.split('_')[0])
        #Add category to label array
        hwLabels.append(classNumStr)
        trainingMat[i,:]=img2vector('trainingDigits/%s'%fileNameStr)
    #Import test set
    testFileList=listdir('testDigits')
    #Error statistics
    errorCount=0.0
    #Number of tests
    mTest=len(testFileList)
    #Cycle training
    for i in range(mTest):
        #Get file name
        fileNameStr=testFileList[i]
        #Remove file suffix
        fileStr=fileNameStr.split('.')[0]
        #Get test category
        classNumStr=int(fileStr.split('_')[0])
        #Convert to 1 * 1024 vector
        vectorUnderTest=img2vector('testDigits/%s'%fileNameStr)
        #Judge with classify0
        classifierResult=classify0(vectorUnderTest,trainingMat,hwLabels,3)
        #Display judgment results and real results
        print ("the classifier came back with:%d,the real answer is :%d"%(classifierResult,classNumStr))
        #Judge whether it is consistent, and the number of inconsistent errors + 1
        if(classifierResult!=classNumStr):errorCount+=1.0
    #Number of output errors
    print("\nthe total number of errors is:%d"%errorCount)
    #Output error rate
    print("\nthe total error rate is :%f"%(errorCount/float(mTest)))

2.2 code implementation

As in the previous experiment, enter cmd in the code directory to open the command prompt
Enter in sequence:
python
import KNN
KNN.handwritingClassTest()

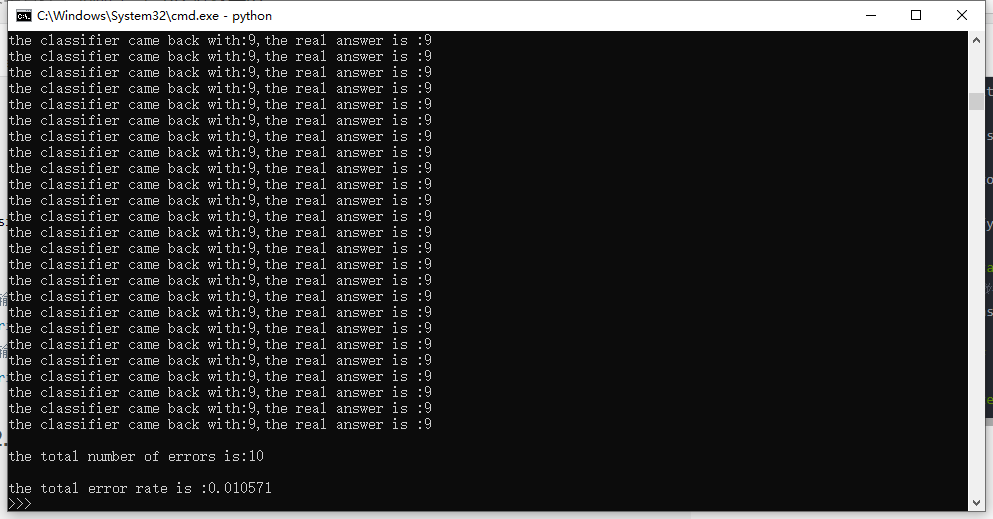
As shown in the figure, the test results generally fluctuate around 1%.

3. Experimental summary

This experiment can clearly see the advantages and disadvantages of k-nearest neighbor algorithm
advantage:
1. Simple and effective
2. Easy to understand
Disadvantages:
1. All data sets must be saved. If the training data set is large, it will consume a lot of storage space
2. Compared with other algorithms, it is very time-consuming to calculate the distance of each data
3. The basic structure information of any data cannot be given, so it is impossible to know what characteristics the average instance sample and typical sample have
Through the advantages and disadvantages, we can find that k-nearest neighbor algorithm is obviously a basic algorithm suitable for beginners' machine learning. It may be further optimized, but its design idea determines its upper limit, so it is difficult to make a huge breakthrough.