Machine Learning Practice 9.2 tree pruning

All the codes in this article can be downloaded from github. You might as well have a Star to thank you. Github code address

I. Introduction

This article will introduce tree pruning techniques based on the construction process of the regression tree in the previous section.

2. Tree pruning

If a tree has too many nodes, it indicates that the model may "over-fit" the data.

The process of avoiding over-fitting by reducing the complexity of the tree is called pruning. As we mentioned in the previous section, setting tolS and tolN is a pre-pruning operation. Another form of pruning requires the use of test sets and training sets, called post pruning. This section will analyze the effectiveness of post-pruning, but first look at the shortcomings of pre-pruning.

2.1 Prepruning

Prepruning has some limitations, such as we now use a new data set.

Data Set Download Address: Data Set Download

Draw the data set with the code in the previous section to see:

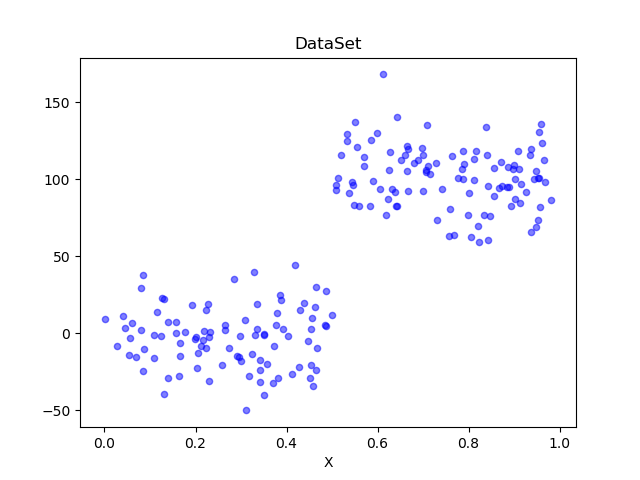
As you can see, this data set is very similar to the first data set we used, but the difference is that the order of magnitude of y is 100 times different and the data distribution is similar, so the tree should be constructed with only two leaf nodes. But if we use the default tolS and tolN parameters to create the tree, you will find that the results are as follows:

As you can see, the constructed tree has many leaf nodes. The reason for this phenomenon is that the stopping condition tolS is very sensitive to the magnitude of the error. If you spend time in the options and average the tolerance of the above errors, you may also get a tree consisting of only two leaf nodes:

As you can see, when the parameter tolS is changed to 10000, the tree is constructed with only two leaf nodes. However, it is obvious that this value needs to be tested continuously. Obviously, it is not a good way to get reasonable results by constantly modifying the stopping conditions. In fact, we are often not even sure what results we need to find. Because for a data set of many dimensions, you don't know how many leaf nodes are needed to build a tree.

It can be seen that pre-pruning has great limitations. Next, we discuss post-pruning, which uses test sets to prune trees. Since no user-specified parameters are required, post-pruning is a more ideal pruning method.

2.2 Post-pruning

The post-pruning method needs to divide the data set into test set and training set. Firstly, the parameters are specified to make the tree large enough and complex enough for pruning. Next, the leaf nodes are found from top to bottom, and the test set is used to determine whether the combination of these leaf nodes can reduce the error of the test set. If so, merge.

The pseudocode for prune() after pruning is as follows:

Based on existing tree segmentation test data:
    If any subset is a tree, then the pruning process is recursive in that subset.
    Calculate the error after merging the current two blade nodes
    Calculating the incorporation error
    If merging reduces errors, merge leaf nodes

To demonstrate post-pruning, we use the ex2.txt file as the training set and the new data set ex2test.txt file as the test set.

Test Set Download Address: Data Set Download

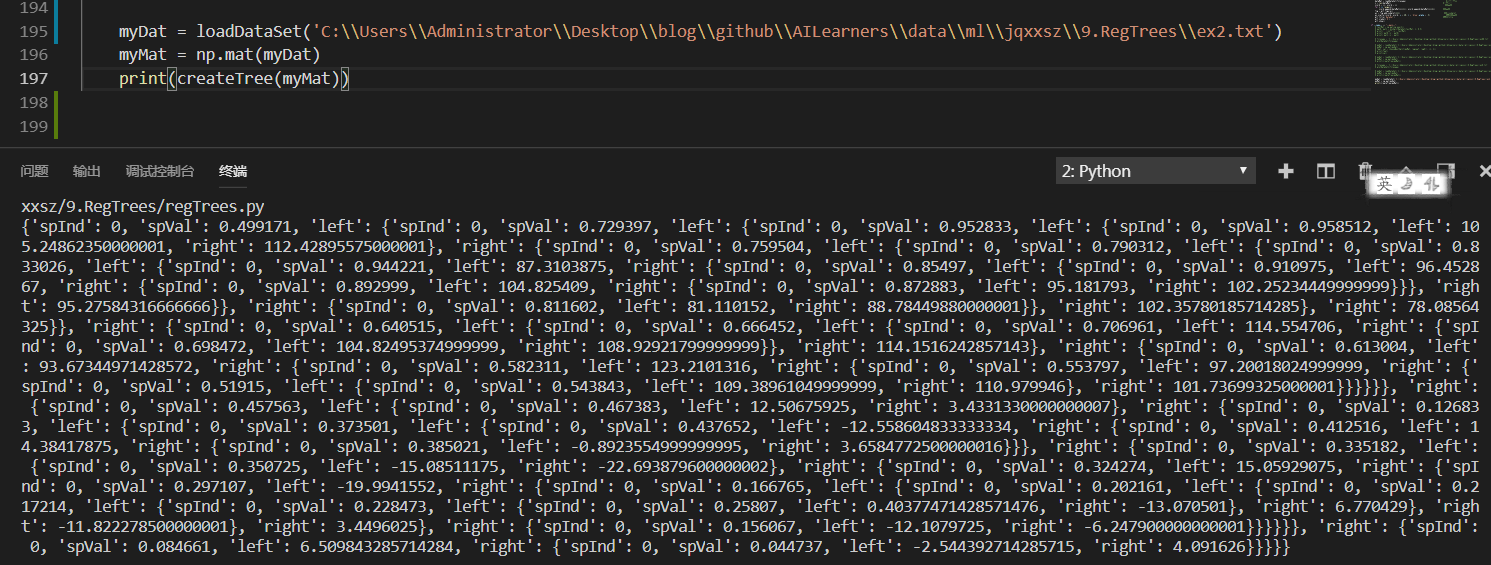
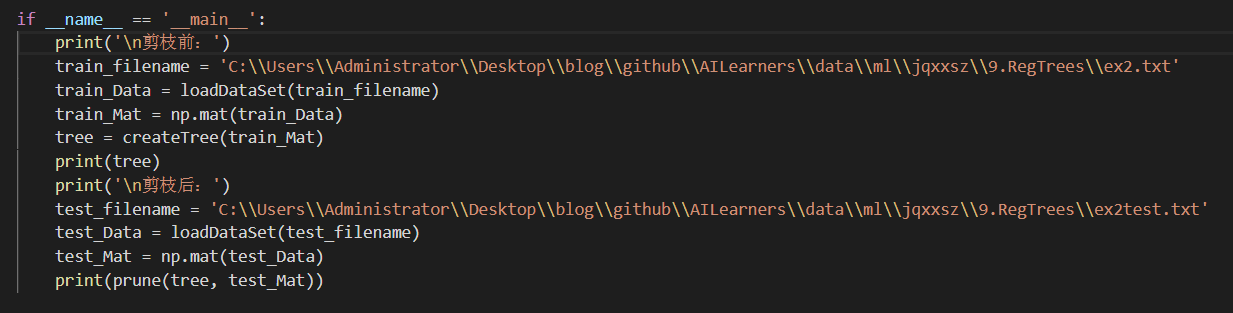
Now we use ex2.txt to train the regression tree, and then use ex2test.txt to prune the regression tree. We need to create three functions isTree(), getMean(), prune(). isTree() is used to test whether the input variable is a tree and return the result of Boolean type. In other words, the function is used to determine whether the node being processed is a leaf node. The second function, getMean(), is a recursive function that traverses the tree from top to bottom until the leaf node. If two leaf nodes are found, their average values are calculated. The function deals with the collapse of the tree (that is, returning the average value of the tree). The third function prune() is a post-pruning function. Establish treePruning.py Write the code as follows:

#!/usr/bin/env python
# -*- encoding: utf-8 -*-
'''
@File    :   treePruning.py
@Time    :   2019/08/05 21:47:48
@Author  :   xiao ming 
@Version :   1.0
@Contact :   xiaoming3526@gmail.com
@Desc    :   Tree pruning after regression
@github  :   https://github.com/aimi-cn/AILearners
'''

# here put the import lib
import matplotlib.pyplot as plt
import numpy as np

'''
@description: Loading data
@param: fileName - file name
@return: dataMat - Data Matrix
'''
def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))                    #Convert to float type
        dataMat.append(fltLine)
    return dataMat

'''
@description: Divide data sets according to features
@param: dataSet - Data aggregation
        feature - Characteristics with Segmentation
        value - The value of this feature 
@return: mat0 - Segmented data set 0
        mat1 - Segmented data set 1
'''
def binSplitDataSet(dataSet, feature, value):
    mat0 = dataSet[np.nonzero(dataSet[:,feature] > value)[0],:]
    mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value)[0],:]
    return mat0, mat1

'''
@description: Generating leaf nodes
@param: dataSet - Data aggregation 
@return: Means of target variables
'''
def regLeaf(dataSet):
    return np.mean(dataSet[:,-1])

'''
@description: Error Estimation Function
@param: dataSet - Data aggregation
@return: Total variance of target variables
'''
def regErr(dataSet):
    return np.var(dataSet[:,-1]) * np.shape(dataSet)[0]

'''
@description: Finding the Best Bivariate Segmentation Function for Data
@param: dataSet - Data aggregation
        leafType - Generating leaf nodes
        regErr - Error Estimation Function
        ops - Tuples of user-defined parameters
@return: bestIndex - Optimal Segmentation Characteristics
        bestValue - Optimum eigenvalue
'''
def chooseBestSplit(dataSet, leafType = regLeaf, errType = regErr, ops = (1,4)):
    import types
    #tolS Allowed Error Decline and the Minimum Sample Number of tolN Segmentation
    tolS = ops[0]; tolN = ops[1]
    #If all current values are equal, exit. (according to the characteristics of set)
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1:
        return None, leafType(dataSet)
    #Row m and column n of statistical data set
    m, n = np.shape(dataSet)
    #By default, the last feature is the best segmentation feature and its error estimation is calculated.
    S = errType(dataSet)
    #They are the index value of the best error, the best feature segmentation and the best feature value, respectively.
    bestS = float('inf'); bestIndex = 0; bestValue = 0
    #Traversing all feature columns
    for featIndex in range(n - 1):
        #Traversing all eigenvalues
        for splitVal in set(dataSet[:,featIndex].T.A.tolist()[0]):
            #Divide data sets according to features and eigenvalues
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            #If the data is less than tolN, exit
            if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue
            #Computational Error Estimation
            newS = errType(mat0) + errType(mat1)
            #If the error estimates are smaller, the eigenvalues and the eigenvalues are updated
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
    #Exit if the error decreases slightly
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    #According to the best segmentation features and eigenvalues, the data set is divided
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    #Exit if the segmented data set is small
    if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
        return None, leafType(dataSet)
    #Returns the best segmentation features and eigenvalues
    return bestIndex, bestValue

'''
@description: Tree Builder Function
@param: dataSet - Data aggregation
        leafType - Establishing the Function of Leaf Node
        errType - Error calculation function
        ops - Tuples that contain trees to build all other parameters
@return: retTree - Constructed regression tree
'''
def createTree(dataSet, leafType = regLeaf, errType = regErr, ops = (1, 4)):
    #Choosing the Best Segmentation Characteristic and Characteristic Value
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    #r If there is no feature, return the eigenvalue
    if feat == None: return val
    #Regression Tree
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    #Divided into left and right datasets
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    #Create left subtree and right subtree
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree  

'''
@description: Determine whether the test input variable is a tree
@param: obj - Test object
@return: Is it a tree?
'''
def isTree(obj):
    import types
    return (type(obj).__name__ == 'dict')

'''
@description: Collapse treatment of trees(That is to say, return the average value of the tree.)
@param: tree - tree
@return: Average Tree Value
'''
def getMean(tree):
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left'] + tree['right']) / 2.0

'''
@description: post-pruning
@param: tree - tree
        test - Test Set
@return: Average Tree Value
'''
def prune(tree, testData):
    #If the test set is empty, the tree is collapsed.
    if np.shape(testData)[0] == 0: return getMean(tree)
    #If there is a left subtree or a right subtree, the data set is partitioned
    if (isTree(tree['right']) or isTree(tree['left'])):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    #Processing left subtrees (pruning)
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
    #Processing right subtree (pruning)
    if isTree(tree['right']): tree['right'] =  prune(tree['right'], rSet)
    #If the left and right nodes of the current node are leaf nodes
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        #Calculating errors without merging
        errorNoMerge = np.sum(np.power(lSet[:,-1] - tree['left'],2)) + np.sum(np.power(rSet[:,-1] - tree['right'],2))
        #Calculate the merged mean
        treeMean = (tree['left'] + tree['right']) / 2.0
        #Calculating merging errors
        errorMerge = np.sum(np.power(testData[:,-1] - treeMean, 2))
        #If the merging error is less than that without merging, the merging
        if errorMerge < errorNoMerge:
            return treeMean
        else: return tree
    else: return tree
 
if __name__ == '__main__':
    print('\n Before pruning:')
    train_filename = 'C:\\Users\\Administrator\\Desktop\\blog\\github\\AILearners\\data\\ml\\jqxxsz\\9.RegTrees\\ex2.txt'
    train_Data = loadDataSet(train_filename)
    train_Mat = np.mat(train_Data)
    tree = createTree(train_Mat)
    print(tree)
    print('\n After pruning:')
    test_filename = 'C:\\Users\\Administrator\\Desktop\\blog\\github\\AILearners\\data\\ml\\jqxxsz\\9.RegTrees\\ex2test.txt'
    test_Data = loadDataSet(test_filename)
    test_Mat = np.mat(test_Data)
    print(prune(tree, test_Mat))

The results are as follows:

It can be seen that a large number of nodes of trees have been pruned off, but not in two parts as expected, which indicates that post-pruning may not be as effective as pre-pruning. Generally, two pruning techniques can be used simultaneously in order to find the best model.

In the next section, we will talk about a project case of model number and tree regression - the comparison of tree regression and standard regression.

AIMI-CN AI Learning Exchange Group [1015286623] for more AI information
Sweep code plus group:

Share technology, enjoy life: our public number computer vision this trivial matter weekly push "AI" series of information articles, welcome your attention!