I. Preface

The previous section describes the principle of machine learning decision tree and how to select the optimal feature as the classification feature. Main contents of this section:

• Decision tree construction
• Decision tree visualization (white box model, neural network is black box model)
• Using decision tree to classify and forecast
• Decision tree storage and reading
• sklearn predicts contact lens types

2, Decision tree construction

**Principle of decision tree generation: * * get the original data set, and then divide the data set based on the best attribute value. Since there may be more than two eigenvalues, there may be more than two branches of data set division. After the first partition, the dataset is passed down to the next node in the branch of the tree. On this node, we can divide the data again, so we can use the principle of recursion to process the data set.
Advantages and disadvantages of decision tree:

• The calculation complexity is not high, and the output results are easy to understand: take ID3 for example, each operation is based on a column of features. After the feature calculation, the next calculation does not consider the optimal feature, and the complexity can be simplified by appropriate pruning;
• It is not sensitive to the missing value in the middle;
• It can process uncorrelated feature data: it is calculated based on each column of features, regardless of the dependency between features.

Types of decision tree algorithms:

ID3
                   

• ID3 does not consider continuous features. For example, length and density are continuous values, which cannot be used in ID3. If it is necessary to use ID3 to get continuous attributes, it is necessary to discretize continuous features by itself
• No consideration for missing values
• For example, if there is a unique identification attribute ID (the ID attribute values of each sample are different), ID3 will choose it as the priority split attribute, which obviously makes the division fully pure, but this division is almost useless for classification

C4.5

• Taking the gain ratio based on the information gain as the splitting criterion of the tree, the problem of ID3's preference to multivalued attribute is solved;
• The discretization of continuous attributes is considered internally, so ID3's preference for multivalued attributes is overcome;
• The automatic processing strategy of missing value is considered internally.

CART

• ID3 and C4.5 can only deal with classification, while CART can deal with classification and regression.

1 ID3 algorithm

The core of    ID3 algorithm is to select the feature of information gain criterion on each node of decision tree and build the decision tree recursively. The specific method is: from the root node (root node) first, calculate the information gain of all possible features for the node, select the feature with the largest information gain as the feature of the node, and establish the sub node according to the different values of the feature; then recursively call the above methods for the sub node to build the decision tree; until the information gain of all features is small or there is no feature to choose, finally get a decision tree. ID3 is equivalent to using maximum likelihood method to select probability model.
                     . It divides the training set D into two subsets D1(A3 value is "yes") and D2(A3 value is "no"). Because D1 has only one sample point of the same type, it becomes a leaf node, and the class of node is marked as "yes".
   for D2, we need to select new features from features A1 (age) and A4 (credit situation), and calculate the information gain of each feature:

• g(D2,A1) = H(D2) - H(D2|A1) = 0.251
• g(D2,A2) = H(D2) - H(D2|A2) = 0.918
• g(D2,A4) = H(D2) - H(D2|A4) = 0.474

                    . Since A2 has two possible values, two sub nodes are derived from this node: a sub node corresponding to "yes" (with work), which contains three samples, and they belong to the same class, so this is a leaf node, and the class is marked as "yes"; another sub node corresponding to "no" (without work), which contains six samples, and they belong to the same class, so this is also a leaf node, class Mark as No. Thus a decision tree is generated. The decision tree only has two features (two internal nodes). The generated decision tree is shown in the following figure: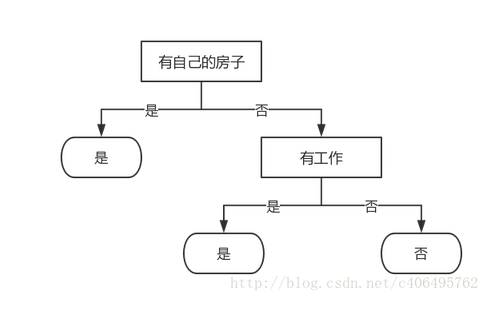

#!/user/bin/env python
# -*- coding:utf-8 -*-
#@Time  : 2020/3/3 10:54
#@Author: fangyuan
#@File: decision tree building decision tree.py

from math import log
import operator

def calcShannonEnt(dataSet):
    numEntires = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntires
        shannonEnt -= prob * log(prob,2)
    return shannonEnt

def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],  # data set
               [0, 0, 0, 1, 'no'],
               [0, 1, 0, 1, 'yes'],
               [0, 1, 1, 0, 'yes'],
               [0, 0, 0, 0, 'no'],
               [1, 0, 0, 0, 'no'],
               [1, 0, 0, 1, 'no'],
               [1, 1, 1, 1, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [2, 0, 1, 2, 'yes'],
               [2, 0, 1, 1, 'yes'],
               [2, 1, 0, 1, 'yes'],
               [2, 1, 0, 2, 'yes'],
               [2, 0, 0, 0, 'no']]
    labels = ['Age','Have a job','Have your own house','Credit situation']
    return dataSet,labels

def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels,featLabels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    featLabels.append(bestFeatLabel)
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),labels,featLabels)
    return myTree

if __name__ == '__main__':
    dataSet,labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet,labels,featLabels)
    print(myTree)

#!/user/bin/env python
# -*- coding:utf-8 -*-
#@Time  : 2020/3/3 15:06
#@Author: fangyuan
#@File: decision tree test classification.py

#!/user/bin/env python
# -*- coding:utf-8 -*-
#@Time  : 2020/3/3 10:54
#@Author: fangyuan
#@File: decision tree building decision tree.py

from math import log
import operator

def calcShannonEnt(dataSet):
    numEntires = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntires
        shannonEnt -= prob * log(prob,2)
    return shannonEnt

def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],  # data set
               [0, 0, 0, 1, 'no'],
               [0, 1, 0, 1, 'yes'],
               [0, 1, 1, 0, 'yes'],
               [0, 0, 0, 0, 'no'],
               [1, 0, 0, 0, 'no'],
               [1, 0, 0, 1, 'no'],
               [1, 1, 1, 1, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [2, 0, 1, 2, 'yes'],
               [2, 0, 1, 1, 'yes'],
               [2, 1, 0, 1, 'yes'],
               [2, 1, 0, 2, 'yes'],
               [2, 0, 0, 0, 'no']]
    labels = ['Age','Have a job','Have your own house','Credit situation']
    return dataSet,labels

"""
//Delete the row data set with value in axis column, adjust the data set and return to the new data set
axis Representation is the first feature value Indicates the value of the corresponding feature
//For example, if axis = 0 value = 1, the new data set returned is (delete the first column in rows 6 to 10)
[0,0,0,'no'],
[0,0,1,'no'],
[1,1,1,'yes'],
[0,1,2,'yes'],
[0,1,2,'yes']
"""
def splitDataSet(dataSet,axis,value):
    # Create a list of returned datasets
    retDataSet = []
    # Traverse data set by row
    for featVec in dataSet:
        # If the axis column value of a row is value
        if featVec[axis] == value:
            # Remove an element axis of the row, such as 1 in column 0 of the above comment
            reducedFeatVec = featVec[:axis]
            # Modify the qualified rows and add them to the returned dataset
            reducedFeatVec.extend(featVec[axis+1:])
            # Add data set after return partition
            retDataSet.append(reducedFeatVec)
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    # Number of characteristic columns is 4
    numFeatures = len(dataSet[0]) - 1
    # Shannon entropy of calculation data set
    baseEntropy = calcShannonEnt(dataSet)
    # information gain
    bestInfoGain = 0.0
    # Index value of optimal feature
    bestFeature = -1
    # Traversal of all features (one column, one column traversal)
    for i in range(numFeatures):
        # Get all values of the ith feature of the dataSet, i.e. the ith column, from top to bottom
        featList = [example[i] for example in dataSet]
        # To create a set set, the elements cannot be repeated. For example, in feature 1, only 0, 1 and 2 represent youth, middle age and old age
        uniqueVals = set(featList)
        # Empirical conditional entropy
        newEntropy = 0.0
        # Calculate information gain
        for value in uniqueVals:
            # Subset after the Division
            subDataSet = splitDataSet(dataSet,i,value)
            # Calculating the probability of subsets
            prob = len(subDataSet) / float(len(dataSet))
            # Calculating the entropy of empirical condition according to the formula
            newEntropy += prob * calcShannonEnt(subDataSet)
        #
        infoGain = baseEntropy - newEntropy
        # print("the gain of the% d feature is%. 3F"% (I, infogain))
        # Calculate information gain
        if(infoGain > bestInfoGain):
            # Update the information gain to find the maximum information gain
            bestInfoGain = infoGain
            # The index value of the feature with the largest gain of recorded information
            bestFeature = i
    # Returns the index value of the feature with the largest information gain
    return bestFeature

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True)
    return sortedClassCount[0][0]

"""
//Recursion using the createTree() function
//In the recursive algorithm, there are two fixed steps: the recursive head and the recursive body
//Recursion header: when not to call your own method, that is, the end condition of recursion
//Recursive body: when do I need to call my own method, that is, call myself
//Advantages: simplify the problem gradually;
//Disadvantages: it will occupy a large number of system stacks, consume a lot of memory, and be much slower than loop when there are many layers of recursive calls
"""
def createTree(dataSet,labels,featLabels):
    # Taking the classification label means that the rightmost element of all row elements is the class label ('no', 'no','yes','yes'...)
    classList = [example[-1] for example in dataSet]
    # Stop dividing if the categories are exactly the same -- the first stop condition
    # list.count() counts the number of times an element in the list appears
    # For example, just using the feature of having your own house can completely determine whether to loan, and other features do not need to continue to be implemented
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # When all features are traversed, and there are several data, the class label with the most frequent occurrence is returned -- the second stop condition
    # If all the features have been used up, and there are still two situations in the category result, i.e. loan or non loan, then the voting method is used to return the result
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # Select the best feature
    bestFeat = chooseBestFeatureToSplit(dataSet)
    # Label of optimal feature
    bestFeatLabel = labels[bestFeat]
    featLabels.append(bestFeatLabel)
    # According to the optimal features of the tag generation tree such as {'has its own house': {}}}
    myTree = {bestFeatLabel:{}}
    # Delete used feature labels
    del(labels[bestFeat])
    # The attribute values of all the optimal features in the training set are obtained. When bestFeat is' own house ', it is the third column of data [0,0,0,1,0,0,0,1,1,1,1,0,0,0]
    featValues = [example[bestFeat] for example in dataSet]
    # Remove duplicate property values, uniqueVal:{0,1}
    uniqueVals = set(featValues)
    # Traverse feature, create decision tree
    # When the optimal feature is' own house ', there are only two classifications of 0 and 1. That is, taking the feature as the root node and 0 and 1 as the branch, this dataset is divided into two sub datasets, which are recursive
    for value in uniqueVals:
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),labels,featLabels)
    return myTree

def classify(inputTree,featLabels,testVec):
    # iteration
    firstStr = next(iter(inputTree))
    secondDict = inputTree[firstStr]
    # Convert label string to index
    # The index() method finds the first element in the current list that matches the firstStr variable
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key],featLabels,testVec)
            else:classLabel = secondDict[key]
    return classLabel

if __name__ == '__main__':
    dataSet,labels = createDataSet()

    print("Optimal characteristic index value:" + str(chooseBestFeatureToSplit(dataSet)))

    featLabels = []
    myTree = createTree(dataSet,labels,featLabels)
    print(myTree)
    testVec = [0,1]
    result = classify(myTree,featLabels,testVec)
    if result == 'yes':
        print('lending')
    if result == 'no':
        print('No lending')

2 write decision tree code

# Using dictionary to represent decision tree
{'Have your own house':{0:{'Have a job':{0:'no',1:'yes'}},1:'yes'}}

Python knowledge accumulation

• Difference between extend and append

>>> li = ['a', 'b', 'c']  
>>> li.extend(['d', 'e', 'f'])   
>>> li  
['a', 'b', 'c', 'd', 'e', 'f']  
>>> len(li)                      
6  
>>> li[-1]  
'f'  
>>> li = ['a', 'b', 'c']  
>>> li.append(['d', 'e', 'f'])   
>>> li  
['a', 'b', 'c', ['d', 'e', 'f']]  
>>> len(li)                      
4  
>>> li[-1]  
['d', 'e', 'f'] 

• next() and iter() functions
  Reference link
  Reference link