Logistic Regression
Fitting some data points with a straight line awakens. The process of fitting is called regression, and this straight line is called the best fit line.
The main idea of using classification is to establish regression formulas to classify boundary lines based on existing data.
The term "regression" here derives from the best fit, which means to find the best set of fitting parameters.
The main idea of using Logistic regression to classify is to establish regression formulas to classify boundary lines based on existing data. The term "regression" here derives from the best fit and indicates that the set of best fit parameters is to be found. When training classifiers, it is necessary to find the best fitting parameters and to use the best optimization algorithm.
General Processes of Logistic Regression
(1) Collect data: collect data in any way.
(2) Preparing data: Because distance calculations are required, data types are required to be numeric. Structured data formats are also best.
(3) Analyzing data: Analyzing data using any method.
(4) Training algorithm: Most of the time will be used for training, the purpose of training is to find the best regression coefficient for classification.
(5) Test the algorithm: Once the training steps are completed, the classification will be fast.
(6) Using algorithms: First, we need to input some data and convert it into corresponding structured values; Then, based on the trained regression coefficients, simple regression calculations can be made for these values to determine which category they belong to. After that, we can do some additional analysis on the categories of output.
Logisic Regression
Advantages: Low computational cost, easy to understand and implement.
Disadvantages: It is easy to underfit and the classification accuracy may not be high.
Applicable data types: numeric and nominal.
1. Classification based on Logistic regression and Sigmoid function
The function we want is to accept all the inputs and then predict the category. For example, in the case of two classes, the above function outputs 0 or 1. This function is called the Heaviside step function, or directly the unit step function. The problem with the Heiveside step function, however, is that it is not continuous and jumps from zero to one instantaneously at the jump point, which is sometimes difficult to handle. Fortunately, another function has similar properties and is mathematically easier to handle, which is the Sigmoid function. The formula for calculating the Sigmoid function is as follows:
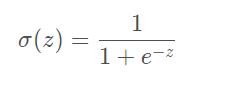
The figure above gives two curves of the Sigmoid function at different coordinate scales. When x is 0, the Sigmoid function value is 0.5. As x increases, the corresponding Sigmoid value approaches 1. As x decreases, the Sigmoid value approaches 0. If the scale of the transverse coordinate is large enough (figure below), the Sigmoid function looks like a step function.
Therefore, in order to implement a Logistic regression classifier, we can multiply a regression coefficient on each feature, then add all the result values together, substitute this sum into the Sigmoid function, and get a value ranging from 0 to 1. Any data greater than 0.5 is grouped into class 1 and less than 0.5 is grouped into class 0. Therefore, logistic regression can also be considered a probability estimate.
2. Determination of optimal regression coefficient based on optimization method
The input to the Sigmoid function is recorded as Z Z z, derived from the following formula: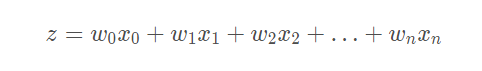
If vector is used, the above formula can be written as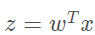
, which means that z-values are obtained by multiplying the corresponding elements of the two numeric vectors and adding them all together. The vector x is the input data to the classifier, and the vector w is the best parameter (coefficient) that we want to find to make the score classifier as accurate as possible. In order to find the optimal parameter, a gradient-up algorithm is used to solve the problem.
1. Gradient Up Algorithm
The gradient rise method is based on the idea that the best way to find the maximum value of a function is to follow the gradient direction of the function. If the gradient is denoted as \nabla, the gradient of the function f (x, y) f (x, y) f (x, y) is represented by the following:
The gradient-up algorithm reassembles the direction of movement after reaching each point. Beginning with P0, after calculating the gradient of the point, the function moves to the next point P1 according to the gradient. At point P1, the gradient is recalculated and moved to P2 along the new gradient direction. Iterate through this loop until the stop condition is met. The gradient operator always ensures that we can choose the best direction of movement during iteration
The gradient-up algorithm in the figure above moves one step in the direction of the gradient. As you can see, the gradient operator always points in the direction where the function value increases the fastest. What is said here is the direction of movement, not the amount of movement. This value is called the step and is recorded as α \ alpha α. In terms of vectors, the iteration formula of the gradient rise algorithm is as follows:
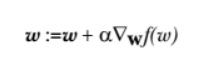
The formula will be iterated until a stop condition is reached, such as the number of iterations reaching a specified value or the algorithm reaching an allowable error range.
Using the testSet.txt dataset, the data is as follows:
The data has two-dimensional characteristics, and the last column is the classification label, which is classified according to the label.
import matplotlib.pylab as plt
import numpy as np
"""
Function description: Load data
"""
def loadDataSet():
# Create Data List
dataMat=[]
# Create tag list
labelMat=[]
# Open File
fr=open('testSet.txt')
# Read line by line
for line in fr.readlines():
# Go back and put it on the list
lineArr=line.strip().split()
# Add data
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
# Add Tags
labelMat.append(int(lineArr[2]))
# Close File
fr.close()
return dataMat,labelMat
"""
Function description: Draw datasets
"""
def plotDataSet():
#Loading datasets
dataMat,labelMat=loadDataSet()
#array converted to numpy
dataArr=np.array(dataMat)
#Number of data
n=np.shape(dataMat)[0]
#Positive Sample
xcord1=[];ycord1=[]
#Negative Samples
xcord2=[];ycord2=[]
#Classify by dataset label
for i in range(n):
#1 is a positive sample
if int(labelMat[i])==1:
xcord1.append(dataArr[i,1])
ycord1.append(dataArr[i,2])
#0 is negative sample
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig=plt.figure()
#Add subplot
ax=fig.add_subplot(111)
#Draw positive samples
ax.scatter(xcord1,ycord1,s=20,c='red',marker='s',alpha=.5)
#Draw negative samples
ax.scatter(xcord2,ycord2,s=20,c='green',alpha=.5)
plt.title('DataSet')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
if __name__=='__main__':
plotDataSet()
The distribution of the data used can be seen from the following figure:
The figure above shows the distribution of the data. Assuming the input of the Sigmoid function is z, then z=W0+W1X1+W2X2 separates the data. X0 is the full 1 vector, X1 is the first column of data, and X2 is the second column of data. If Z=0, then 0=W0+W1X1+W2X2, horizontal coordinate is X1, vertical coordinate is X2, and unknown parameters W0, W1, W2 are the required regression coefficients.
2. Training algorithm: use gradient rise to find the best parameters
There are 100 sample points in the figure above, each of which contains two descriptive features: X1 and X2. On this dataset, we will use the gradient-rise method to find the best regression coefficients, that is, the best parameters to fit the Logistic regression model.
The pseudocode for the gradient rise method is as follows:
Each regression coefficient is initialized to 1
Repeat R times:
Calculate gradients for the entire dataset
Use alpha × gradient updates the vector of regression coefficients
Return regression coefficients
'''
Parameters:
inX - data
Returns:
sigmoid function
'''
# Function description: sigmoid function
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
'''
Parameters:
dataMatIn - data set
classLabels - Data Label
Returns:
'''
# Function description: Gradient rise algorithm
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #mat converted to numpy
labelMat = np.mat(classLabels).transpose() #Convert to numpy mat and transpose
m, n = np.shape(dataMatrix) #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
alpha = 0.001 #The moving step, the learning rate, controls the magnitude of the update.
maxCycles = 500 #Maximum number of iterations
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #Gradient Up Vectorization Formula
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #Converts a matrix to an array, returning an array of weights
A set of regression coefficients for the Gradient Up algorithm can be found:
>>> [[ 4.12414349] [ 0.48007329] [-0.6168482 ]]
3. Analyzing data: drawing decision boundaries
A set of regression coefficients has been worked out above, and he has determined that only intervals are visible for different categories of data.
'''
Parameters:
weights - Weight parameter array
Returns:
nothing
'''
# Function description: Draw datasets
def plotBestFit(weights):
dataMat, labelMat = loadDataSet() #Loading datasets
dataArr = np.array(dataMat) #Array array converted to numpy
n = np.shape(dataMat)[0] #Number of data
xcord1 = []; ycord1 = [] #Positive Sample
xcord2 = []; ycord2 = [] #Negative Samples
for i in range(n): #Classify by dataset label
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1 is a positive sample
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0 is negative sample
fig = plt.figure()
ax = fig.add_subplot(111) #Add subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#Draw positive samples
ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5) #Draw negative samples
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') #Draw title
plt.xlabel('X1'); plt.ylabel('X2') #Draw label
plt.show()
As you can see from the figure above, there are only two to four points that are wrong. However, although the example is simple and the dataset is small, this method requires a lot of computation (300 multiplies).
4. Training algorithm: Random gradient rise
Gradient Up algorithm: The entire dataset needs to be traversed every time the regression coefficients are updated, which is too complex on billions of samples.
Improvement: Random Gradient Up algorithm: Update regression coefficients with only one sample point at a time.
Since the classifier can be updated incrementally when new samples arrive, the Random Gradient Up algorithm is an online learning algorithm. In contrast to online learning, processing all data at once is called batch processing.
The Random Gradient Up algorithm can be written as pseudocode as follows:
All regression coefficients are initialized to 1
For each sample in the dataset
Calculate the gradient of the sample
Use alpha × gradient updates regression coefficient values
Return the regression coefficient value
'''
Parameters:
dataMatrix - Data Array
classLabels - Data Label
Returns:
weights - Array of regression coefficients obtained(Optimal parameters)
'''
def stocGradAscent0(dataMatrix, classLabels):
m,n = np.shape(dataMatrix) #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
alpha = 0.01
weights = np.ones(n) #Parameter Initialization
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights)) #Select a randomly selected sample and calculate h
error = classLabels[i] - h #calculation error
weights = weights + alpha*error*dataMatrix[i] #Updating regression coefficients
return weights
The fit is not as good as the gradient-up algorithm. The classifier here misses one-third of the samples. The result of the gradient-up algorithm is 500 iterations over the entire dataset.
Improved Random Gradient Rising Algorithm
(1) Alpha is adjusted at each iteration, which mitigates data fluctuations or high frequency fluctuations in the above fluctuation graph. In addition, although alpha decreases with the number of iterations, it never decreases to zero because we add a constant term to our formula.
(2) Modify to randIndex update, where the regression coefficient is updated by randomly selecting a sample pull. This method will reduce periodic fluctuations. This method randomly picks a value from the list at a time and then deletes it from the list (for the next iteration).
The improved algorithm also adds an iteration number as the third parameter. If this parameter is not given, the algorithm will iterate 150 times by default. If given, the algorithm iterates over the new parameter values.
'''
Parameters:
dataMatrix - Data Array
classLabels - Data Label
numIter - Number of iterations
Returns:
weights - Array of regression coefficients obtained(Optimal parameters)
'''
# Function description: improved random gradient rise algorithm
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = np.shape(dataMatrix) #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
weights = np.ones(n) #Parameter Initialization
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 #Reduce the size of alpha by 1/(j+i) at a time.
randIndex = int(random.uniform(0,len(dataIndex))) #Random sample selection
h = sigmoid(sum(dataMatrix[randIndex]*weights)) #Select a randomly selected sample and calculate h
error = classLabels[randIndex] - h #calculation error
weights = weights + alpha * error * dataMatrix[randIndex]#Updating regression coefficients
del(dataIndex[randIndex]) #Delete used samples
return weights #Return
5. Relationship between regression coefficient and iteration number
import matplotlib.pylab as plt
import numpy as np
import random
from matplotlib.font_manager import FontProperties
"""
Function description: Load data
"""
def loadDataSet():
# Create Data List
dataMat=[]
# Create tag list
labelMat=[]
# Open File
fr=open('testSet.txt')
# Read line by line
for line in fr.readlines():
# Go back and put it on the list
lineArr=line.strip().split()
# Add data
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
# Add Tags
labelMat.append(int(lineArr[2]))
# Close File
fr.close()
return dataMat,labelMat
"""
Function description: sigmoid function
"""
def sigmoid(inX):
return 1.0/(1+np.exp(-inX))
"""
Function description: Gradient rise algorithm
"""
def gradAscent(dataMatIn,classLabels):
#mat converted to numpy
dataMatrix=np.mat(dataMatIn)
# mat converted to numpy and transposed
labelMat=np.mat(classLabels).transpose()
#Returns the size of the dataMatrix with m as rows and n as columns
m,n=np.shape(dataMatrix)
#Moving step, or learning rate, controls the speed at which parameters are updated
alpha=0.01
#Maximum number of iterations
maxCycles=500
weights=np.ones((n,1))
weights_array = np.array([])
for k in range(maxCycles):
#Gradient Up Vectorization Formula
h=sigmoid(dataMatrix*weights)
error=labelMat-h
weights=weights+alpha*dataMatrix.transpose()*error
weights_array = np.append(weights_array, weights)
weights_array = weights_array.reshape(maxCycles, n)
#Converts the matrix to an array and returns the weight parameter
return weights.getA(),weights_array
"""
Function description: Draw datasets
"""
def plotBestFit(weights):
#Loading datasets
dataMat,labelMat=loadDataSet()
dataArr=np.array(dataMat)
#Number of data
n=np.shape(dataMat)[0]
#Positive Sample
xcord1=[]
ycord1=[]
#Negative Samples
xcord2=[]
ycord2=[]
#Classify by dataset label
for i in range(n):
#1 is a positive sample
if int(labelMat[i])==1:
xcord1.append(dataArr[i,1])
ycord1.append(dataArr[i,2])
#0 is negative sample
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig = plt.figure()
# Add subplot
ax = fig.add_subplot(111)
# Draw positive samples
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
# Draw negative samples
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
x=np.arange(-3.0,3.0,0.1)
y=(-weights[0]-weights[1]*x)/weights[2]
ax.plot(x,y)
plt.title('BestFit')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
"""
Function description: improved random gradient rise algorithm
"""
def stocGradAscent1(dataMatix,classLabels,numIter=150):
m,n=np.shape(dataMatix)
weights=np.ones(n)
weights_array=np.array([])
for j in range(numIter):
dataIndex=list(range(m))
for i in range(m):
#Reduce alpha size
alpha=4/(1.0+j+i)+0.01
#Random sample selection
randIndex=int(random.uniform(0,len(dataIndex)))
#Select randomly selected samples and calculate h
h=sigmoid(sum(dataMatix[randIndex]*weights))
#calculation error
error=classLabels[randIndex]-h
#Updating regression coefficients
weights=weights+alpha*error*dataMatix[randIndex]
#Add regression coefficients to the array
weights_array=np.append(weights_array,weights,axis=0)
#Delete used samples
del(dataIndex[randIndex])
#Change Dimension
weights_array=weights_array.reshape(numIter*m,n)
#Return
return weights,weights_array
"""
Function Description:Draw the relationship between regression coefficient and iteration number
Parameters:
weights_array1 - Regression Coefficient Array 1
weights_array2 - Regression Coefficient Array 2
Returns:
nothing
"""
def plotWeights(weights_array1,weights_array2):
#Format Chinese Characters
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
#Separate fig canvas into 1 row and 1 column, do not share x and y axes, fig canvas size is (13,8)
#When nrow=3 and nclos=2, the fig canvas is divided into six regions, and axs[0][0] represents the first row and the first column
fig, axs = plt.subplots(nrows=3, ncols=2,sharex=False, sharey=False, figsize=(20,10))
x1 = np.arange(0, len(weights_array1), 1)
#Draw the relationship between w0 and number of iterations
axs[0][0].plot(x1,weights_array1[:,0])
axs0_title_text = axs[0][0].set_title(u'Gradient Up algorithm: relationship between regression coefficient and iteration number',FontProperties=font)
axs0_ylabel_text = axs[0][0].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
#Draw the relationship between w1 and the number of iterations
axs[1][0].plot(x1,weights_array1[:,1])
axs1_ylabel_text = axs[1][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
#Draw the relationship between w2 and number of iterations
axs[2][0].plot(x1,weights_array1[:,2])
axs2_xlabel_text = axs[2][0].set_xlabel(u'Number of iterations',FontProperties=font)
axs2_ylabel_text = axs[2][0].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
x2 = np.arange(0, len(weights_array2), 1)
#Draw the relationship between w0 and number of iterations
axs[0][1].plot(x2,weights_array2[:,0])
axs0_title_text = axs[0][1].set_title(u'Improved Random Gradient Rising Algorithm: Regression Coefficient and Number of Iterations',FontProperties=font)
axs0_ylabel_text = axs[0][1].set_ylabel(u'W0',FontProperties=font)
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
#Draw the relationship between w1 and the number of iterations
axs[1][1].plot(x2,weights_array2[:,1])
axs1_ylabel_text = axs[1][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
#Draw the relationship between w2 and number of iterations
axs[2][1].plot(x2,weights_array2[:,2])
axs2_xlabel_text = axs[2][1].set_xlabel(u'Number of iterations',FontProperties=font)
axs2_ylabel_text = axs[2][1].set_ylabel(u'W1',FontProperties=font)
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights1,weights_array1 = stocGradAscent1(np.array(dataMat), labelMat)
weights2,weights_array2 = gradAscent(dataMat, labelMat)
plotWeights(weights_array1, weights_array2)
The improved Random Gradient Up algorithm randomly selects sample points, so the results are different each time, but the general trend is the same.
The improved random gradient rise algorithm has better convergence:
We have a total of 100 sample points, and the number of iterations of the improved random gradient rise algorithm is 150. The reason the graph shows 15,000 iterations is that the regression coefficients are updated with one sample. Therefore, 150 iterations are equivalent to 150*100=15,000 updates of the regression coefficient. In short, iterate 150 times and update 15,000 regression parameters. As you can see from the regression results of the improved Random Gradient Rising algorithm on the left side of the figure above, the regression coefficients have actually converged by updating 2000 times. The regression coefficients have converged when traversing the entire dataset 20 times. Training has been completed.
Let's look at the regression performance of the gradient-up algorithm on the right side of the image above, which traverses the entire dataset each time the regression coefficients are updated. As you can see from the graph, the regression coefficients converge when the number of iterations is more than 300. Compact, it will converge when it traverses the entire dataset 300 times.
The improved random gradient rise algorithm converges on the 20th traversal of the dataset. The gradient-up algorithm does not converge until it traverses the dataset 300 times.
Summary: For logistic regression, it is actually a function with a regression model, for input and output, so only the parameters in it need to be estimated. For parameter estimation, it involves cost function, which can be estimated with maximum likelihood. Since, from a probability point of view, for known samples, it is generally assumed that the probability of getting these samples under a certain parameter must be relatively large, the estimation probability can be maximized by selecting the largest parameter in the parameter set. Finally, the gradient descent method can be used, and random gradient descent can also be used to improve efficiency, since this is the maximum value, and only the gradient direction symbol needs to be changed to +.