Classification algorithm - logistic regression

[also an iterative method, self updating w]

Linear input to classification problem:

Input: the formula of linear regression is used as the input of logical regression

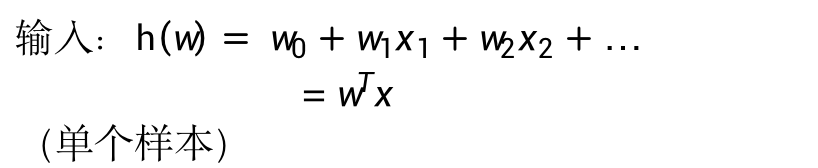
sigmoid function:

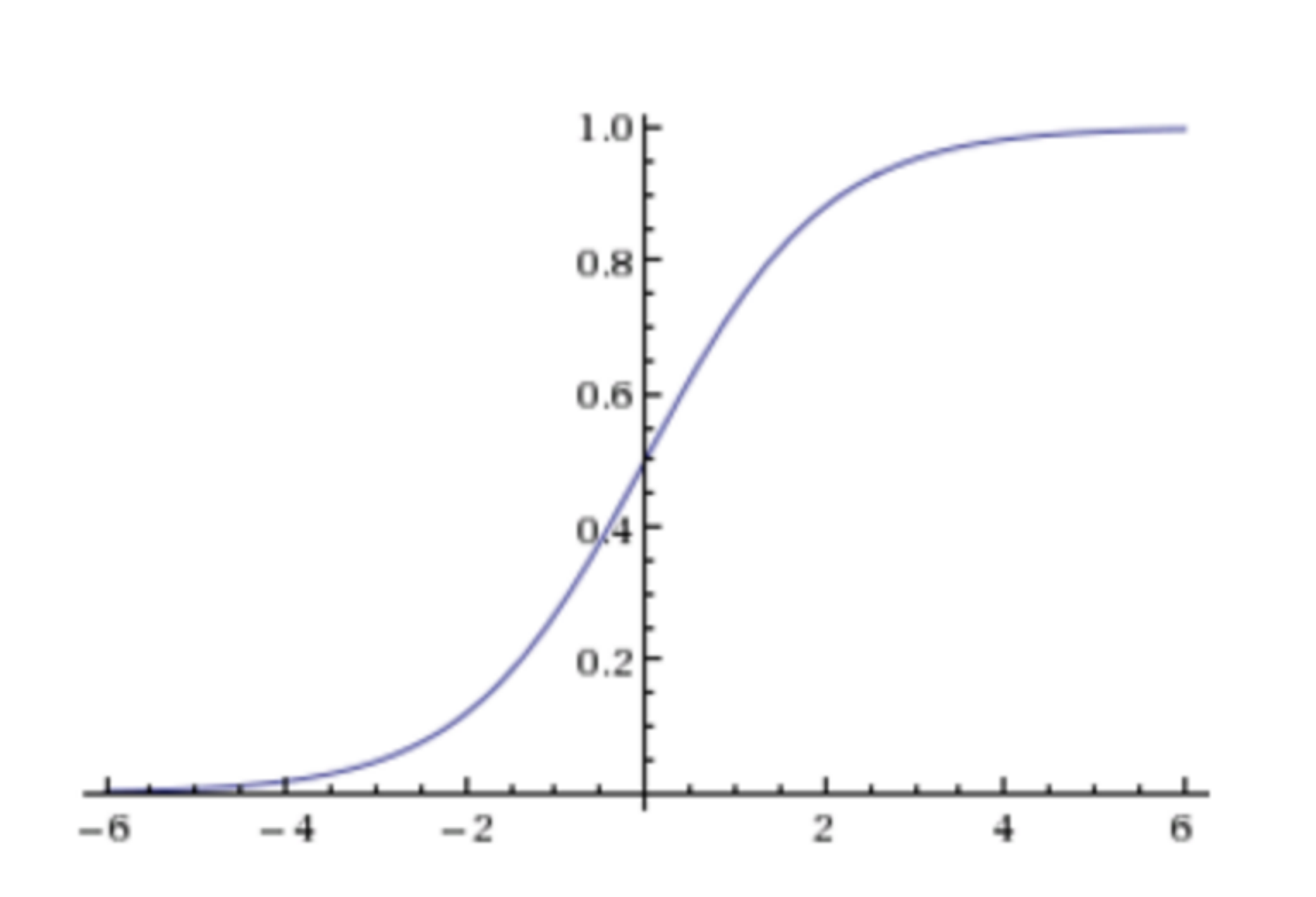
Logistic regression formula: [that is, how sigmoid converts input into probability value]

e: 2.71

Z = result of regression

Output: probability value can also be obtained

Loss function and optimization of logistic regression

It is the same as the principle of linear regression, but because it is a classification problem, the loss function is different and can only be solved by gradient descent

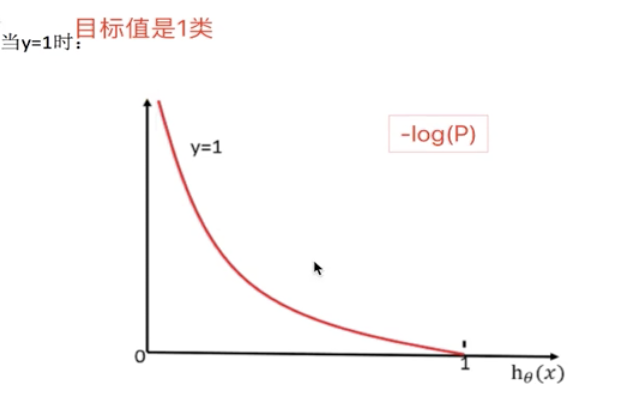
[when the target value is a class, the closer the probability is to 1, the smaller the loss function]  

[which category has few samples in the second category, and the judgment probability refers to this category]

 

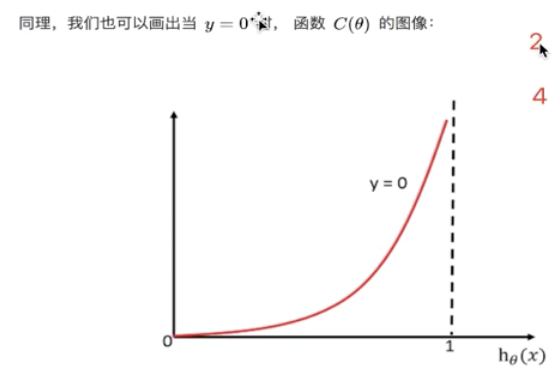
[the target value is zero, and the closer the probability is to 1, the greater the loss function]

  [logistic regression only judges whether a category is or not, and judges the probability of belonging to a category. h (x) all refers to judging a category, so the image is opposite, so the above situation can occur]

[similar to information entropy, the smaller the better]

[it is also to update the weight]  

Comparative analysis of loss function:

Syntax:

sklearn.linear_model.LogisticRegression

sklearn.linear_model.LogisticRegression(penalty = 'l2', C = 1.0) [with regularization]

Logistic regression classifier

coef_: regression coefficient

C: Regularization gradient

penalty: regularization term

Application: [only applicable to category II]

• Advertising click through rate
• Judge the user's gender
• Predict whether users will buy a given product category
• Judge whether a comment is positive or negative

[logistic regression is a powerful tool to solve binary classification problems]

Case:

Tumor prediction in benign and malignant breast cancer

Download address of original data: https://archive.ics.uci.edu/ml/machine-learning-databases/

Data Description:

(1) 699 samples, a total of 11 columns of data. The first column uses the retrieved id, the last 9 columns are the medical characteristics related to tumor, and the last column represents the value of tumor type.

(2) Contains 16 missing values, use "?" Mark.

Target value:

Malignant tumor was selected as the target value as a positive example

technological process:

1. Online data acquisition tool (pandas)
2. Data missing value processing and standardization
3. LogisticRegression estimator process

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np


def logistic():
    """
    Logistic regression was used to make binary classification for cancer prediction (according to the attribute characteristics of cells)
    :return: NOne
    """
    # Construct column label name
    column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']

    # Read data
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column)

    print(data)

    # Processing missing values
    data = data.replace(to_replace='?', value=np.nan)

    data = data.dropna()

    # Data segmentation
    x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)

    # Standardized treatment
    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # Logistic regression prediction
    lg = LogisticRegression(C=1.0)

    lg.fit(x_train, y_train)

    print(lg.coef_)

    y_predict = lg.predict(x_test)

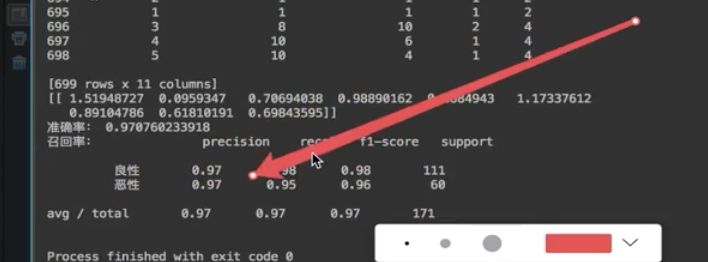
    print("Accuracy:", lg.score(x_test, y_test))

    print("Recall rate:", classification_report(y_test, y_predict, labels=[2, 4], target_names=["Benign", "malignant"]))#Remember label

    return None


if __name__ == "__main__":
    logistic()

The results show that:

  Result analysis:

When it comes to cancer, we're thinking about recall rates