Title Description

For example, there are N small root heaps at the beginning. Each heap contains only one number. Next, two operations need to be supported:

Operation 1:1 x y merges the small root heap where the number x and y are located (ignoring this operation if the number x or Y has been deleted or the number x and y are in one heap)

Operation 2:2x outputs the minimum number of heaps where the number x is located and deletes it (output-1 ignores deletion if the number x has been deleted)

Input and output format

The first line contains two positive integers, N and M, representing the number of small root heaps at the beginning and the number of subsequent operations, respectively.

The second line contains N positive integers, where the first positive integer represents the number contained and contained only at the beginning of the second root heap.

Next, M lines have two or three positive integers per line, representing an operation in the following format:

Operation 1:1 x y

Operation 2:2x

The output contains several line integers corresponding to the results of each operation 2 in turn.

Input and Output Samples

5 5
1 5 4 2 3
1 1 5
1 2 5
2 2
1 4 2
2 2

1
2

Explain

When there are multiple minimum values in the heap, delete the front of the original sequence first, otherwise it will affect subsequent operation 1 leading to WA.

Space-time constraints: 1000ms,128M

Data size:

For 30% of the data: N<=10, M<=10

For 70% of the data: N<=1000, M<=1000

For 100% data: N <= 100000, M <= 100000

Sample description:

Initially, the five small root heaps are {1}, {5}, {4}, {2}, {3}.

In the first operation, the small root heap of the first number is merged with the small root heap of the fifth number, so it becomes four small root heaps: {1,3}, {5}, {4}, {2}.

In the second operation, the small root heap where the second number is located is merged with the small root heap where the fifth number is located, so it becomes three small root heaps: {1,3,5}, {4}, {2}.

In the third operation, the minimum value of the small root heap where the second number is located is output and deleted, so output 1, the first number is deleted, and the three small root heaps are {3,5}, {4}, {2}.

In the fourth operation, the root heap of the fourth number is merged with the root heap of the second number, so it becomes two small root heaps: {2,3,5}, {4}.

In the fifth operation, the minimum value of the small root heap where the second number is located is output and deleted, so output 2, the fourth number is deleted, and the two small root heaps are {3,5}, {4}.

So the output is 1 and 2 in turn.

First of all, the title of the title tells us clearly that this is a template question.

It's a template question, so we should start from theory, popularize common sense, and finally get a long string of code (crazy recitation).

But here, I will not talk about the basic posture of the left-leaning tree. (Actually, I will not.) If necessary, Baidu itself.~~~~~~~~~~

What I'm introducing here is the solution of "pbds"?

If you don't know pbds, please Poke here，Here，And here.

Obviously, this problem is not difficult at all. Maybe some children's shoes have been made according to the posture of pbds.

Now that everyone knows, go straight to the code:

 1 //
 2 #include <bits/stdc++.h>
 3 #include <ext/pb_ds/priority_queue.hpp>
 4 using namespace std;
 5 using namespace __gnu_pbds;
 6 typedef unsigned long long ll;
 7 #define ri register ll
 8 
 9 struct A
10 {
11     ll x;
12     ll rank;
13     bool operator< (const A& p)const
14     {
15         if(x==p.x)
16         {
17             return rank>p.rank;
18         }
19         return x>p.x;
20 //        */
21     }
22 };
23 
24 __gnu_pbds::priority_queue<A,less<A>,pairing_heap_tag> q[100005];
25 ll n,m;
26 ll father[100005];
27 bool vis[100005];
28 
29 ll findf(ll a)
30 {
31     ri k=a;
32     while(father[k]!=k)
33     {
34         k=father[k];
35     }
36     father[a]=k;
37     return k;
38 }
39 
40 void joinf(ll x,ll y)
41 {
42     ri xx=findf(x);
43     ri yy=findf(y);
44     father[yy]=xx;
45 }
46 
47 signed main()
48 {
49     ios::sync_with_stdio(0),cin.tie(0);
50     cin>>n>>m;
51     for(ri i=1;i<=n;i++)
52     {
53         ri p;cin>>p;
54         q[i].push((A){p,i});
55         father[i]=i;
56     }
57     
58     for(ri i=1;i<=m;i++)
59     {
60         ri rerinput;cin>>rerinput;
61         if(rerinput==1)
62         {
63             ri x,y;cin>>x>>y;
64             ri xx=findf(x);
65             ri yy=findf(y);
66             if(q[xx].size()>q[yy].size())swap(xx,yy);
67             q[xx].join(q[yy]);
68             joinf(xx,yy);
69         }
70         else if(rerinput==2)
71         {
72             ri k;cin>>k;
73             if(vis[k])
74             {
75                 cout<<-1<<'\n';
76                 continue;
77             }
78             ri wh=findf(k);
79             cout<<q[wh].top().x<<'\n';
80             vis[q[wh].top().rank]=1;
81             q[wh].pop();
82         }
83     }
84     
85 //    */
86     return 0;
87 }
88 //

Then Kesen gets the following results:

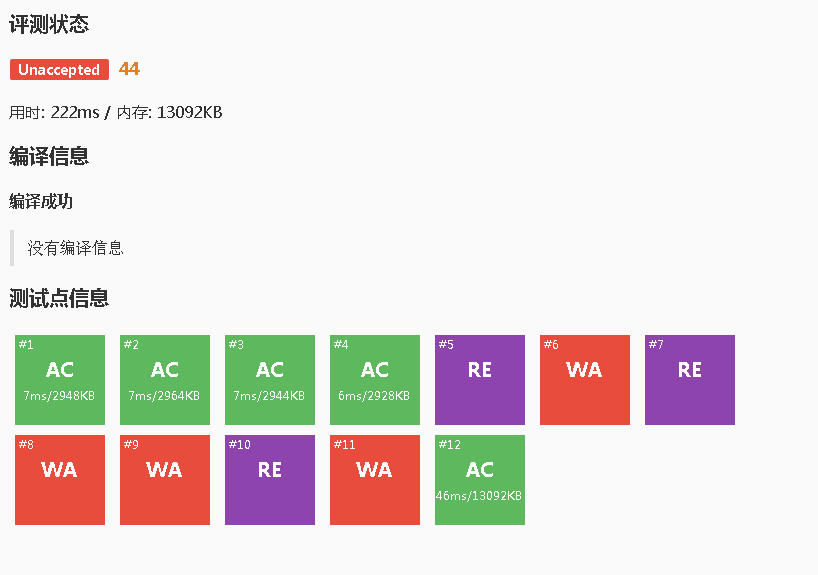
Good and good.

My fault, my fault.

There must be something I missed out on.

Re-examine the title: I found that I had missed the parentheses behind Operation 1.

So I changed it again, adding 66,67 lines.

 1 //
 2 #include <bits/stdc++.h>
 3 #include <ext/pb_ds/priority_queue.hpp>
 4 using namespace std;
 5 using namespace __gnu_pbds;
 6 typedef unsigned long long ll;
 7 #define ri register ll
 8 
 9 struct A
10 {
11     ll x;
12     ll rank;
13     bool operator< (const A& p)const
14     {
15         if(x==p.x)
16         {
17             return rank>p.rank;
18         }
19         return x>p.x;
20 //        */
21     }
22 };
23 
24 __gnu_pbds::priority_queue<A,less<A>,pairing_heap_tag> q[100005];
25 ll n,m;
26 ll father[100005];
27 bool vis[100005];
28 
29 ll findf(ll a)
30 {
31     ri k=a;
32     while(father[k]!=k)
33     {
34         k=father[k];
35     }
36     father[a]=k;
37     return k;
38 }
39 
40 void joinf(ll x,ll y)
41 {
42     ri xx=findf(x);
43     ri yy=findf(y);
44     father[yy]=xx;
45 }
46 
47 signed main()
48 {
49     ios::sync_with_stdio(0),cin.tie(0);
50     cin>>n>>m;
51     for(ri i=1;i<=n;i++)
52     {
53         ri p;cin>>p;
54         q[i].push((A){p,i});
55         father[i]=i;
56     }
57     
58     for(ri i=1;i<=m;i++)
59     {
60         ri rerinput;cin>>rerinput;
61         if(rerinput==1)
62         {
63             ri x,y;cin>>x>>y;
64             ri xx=findf(x);
65             ri yy=findf(y);
66             if(vis[x]||vis[y])continue;
67             if(xx==yy)continue;
68             if(q[xx].size()>q[yy].size())swap(xx,yy);
69             q[xx].join(q[yy]);
70             joinf(xx,yy);
71         }
72         else if(rerinput==2)
73         {
74             ri k;cin>>k;
75             if(vis[k])
76             {
77                 cout<<-1<<'\n';
78                 continue;
79             }
80             ri wh=findf(k);
81             cout<<q[wh].top().x<<'\n';
82             vis[q[wh].top().rank]=1;
83             q[wh].pop();
84         }
85     }
86     
87 //    */
88     return 0;
89 }
90 //

Then we had a good time. __AC code__

But!!!

--Take a look Title Solution.

The dalao s have talked in great detail (they don't understand at all).

From the vast code, I found an important sentence——————

—————— dalao made another concluding remark.

I was so outgoing that I removed the path compression in the above code.

Result:

Well, I don't know why.

But my code seems to need path compression droplets.

Summary:

This essay tells us that we should look at the topic carefully and consider the limitations given by the topic.

In addition, line 68 of the AC code reads "if (q [xx]. size ()> Q [yy]. size ()" swap (xx, yy); "this seems to have to be q [xx]. size ()< Q [yy]. size ().

But to be honest, I'm not sure.

If dalao knows about it, he'll ask for advice.~~