Title Description

C has n large cities and m roads, each of which connects two cities. There is at most one road directly connected between any two cities. Some of the m roads are one-way roads, some are two-way roads, and the number of two-way roads is also counted as one.

Country C is a vast country with different resource distribution, which leads to different prices of the same commodity in different cities. However, the buying and selling prices of the same commodity in the same city are always the same.

A long, a businessman, came to visit country C. When he learned that the price of the same commodity may be different in different cities, he decided to use the price difference of the commodity in different cities to earn back a little travel expenses while traveling. Set the number of n cities in country C from 1~ 1n, Aaron decided to start from city 1, and finally finish his trip in city n. In the process of tourism, any city can go through multiple times, but it is not required to go through all n cities. Aaron earns his traveling expenses through such a way of trade: he will choose a passing city to buy his favorite commodity, crystal ball, and sell the crystal ball in another passing city, using the difference earned as his traveling expenses. As a long mainly came to visit country C, he decided that this trade would only be carried out once at most. Of course, he did not need to carry out trade without earning the difference.

Suppose C has five big cities, and the city number and road connection are shown in the figure below. The one-way arrow indicates that this road is one-way traffic, and the two-way arrow indicates that this road is two-way traffic.

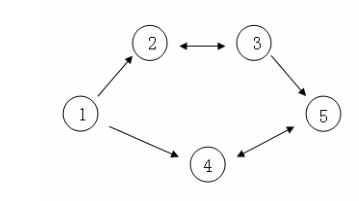
Suppose that the price of crystal balls in 1-1n cities is 4,3,5,6,1 respectively.
A long can choose one of the following routes: 1 - > 2 - > 3 - > 5, and buy crystal balls at the price of 3 in No. 2 City, and sell crystal balls at the price of 5 in No. 3 city. The amount of travel expenses earned is 2.

A long can also choose one of the following routes 1 - > 4 - > 5 - > 4 - > 5, and buy the crystal ball at the price of 1 when he arrives at No. 5 city for the first time, and sell the crystal ball at the price of 6 when he arrives at No. 4 city for the second time. The amount of travel expenses earned is 5.

Now, the price of crystal ball in n cities, the information of m roads (the number of two cities connected by each road and the traffic condition of this road) are given. Please tell Aaron how much travel he can earn at most.

Input format

The first line contains two positive integers, n and m, separated by a space, representing the number of cities and roads respectively.

In the second line, there are n positive integers, each of which is separated by a space, indicating the commodity prices of these n cities in the order of label.

Next m lines, each line has three positive integers x,y,z separated by a space between each two integers. If z=1, it means that this road is a one-way road between city x and city y; if z=2, it means that this road is a two-way road between city x and city y.

Output format

An integer representing the maximum amount of travel that can be earned. If there is no trade, output 0.

Example of input and output

Input #1

5 5 
4 3 5 6 1 
1 2 1 
1 4 1 
2 3 2 
3 5 1 
4 5 2 

Output #1

5

Analysis & Description:

This question is only suitable if SPFA is used, and it is explained by a big guy in the school,

Only then did I know:

This problem uses two pictures: one is the original picture and the other is the reverse picture. In addition, we need to run SPFA twice to calculate the minimum and maximum value of trade, and at last to find the maximum (the difference between the maximum and the minimum value), which is the optimal trade.

CODE:

This is probably the longest code I've typed.

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,k,a[100100],maxn[1000100]/*Maximum array*/,minn[1000100]/*Minimum value array*/,v[1010001],f[1000100],ans;
struct node{
	int x,y,next,w;
}c[1000010],b[1000010];
int tot,tot2,head1[1001000],head2[1001000];//These variables have two, two graphs, twice spfa
void add(int x,int y,int w)
{
	tot++;
	b[tot].x=x;
	b[tot].y=y;
	b[tot].w=w;
	b[tot].next=head1[x];
	head1[x]=tot;
	//First adjacency table
}
void add2(int x,int y,int w)
{
	tot2++;
	c[tot2].x=x;
	c[tot2].y=y;
	c[tot2].w=w;
	c[tot2].next=head2[x];
	head2[x]=tot2;
	//Second adjacency table
}
void spfa(int x)
{
    //spfa minimum
	memset(minn,0x7f,sizeof(minn));  //initial value
	minn[x]=a[x];
	v[x]=1;
	f[1]=x;
	int head=0,tail=1;
	while(head<tail)  //Similar to the implementation of broad search
	{
		head=head%100010+1;
		int x2=f[head];
		for(int i=head1[x2];i;i=b[i].next)  //Adjacency list
		{
			if(minn[b[i].y]>min(a[b[i].y],minn[x2]))
			{
				minn[b[i].y]=min(a[b[i].y],minn[x2]);  //Seeking minimum
				if(!v[b[i].y])
				{
					tail++;  //Join the team
					v[b[i].y]=1;
					f[tail]=b[i].y;
				}
			}
		}
		v[x2]=0; 
	}
}
void spfa2(int x)
{
	//Maximum spfa
	int head=0,tail=1;
	memset(v,0,sizeof(v));  //initial value
	maxn[x]=a[x];
	v[x]=1;
	f[1]=x;
	while(head<tail)
	{
		head=head%100010+1;
		int x2=f[head];
		for(int i=head2[x2];i;i=c[i].next)
		{    //Adjacency list
			if(maxn[c[i].y]<max(a[c[i].y],maxn[x2]))
			{
				maxn[c[i].y]=max(a[c[i].y],maxn[x2]);  //Seeking maximum
				if(v[c[i].y]==0)
				{
					tail++;  //Continue to join the team
					v[c[i].y]=1;
					f[tail]=c[i].y;
				}
			}
		}
		v[x2]=0;
	}
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	for(int i=1;i<=m;i++)
	{
		int x,y,k;
		cin>>x>>y>>k;
		if(k==1)
		{
			add(x,y,a[y]);
			add2(y,x,a[x]);
		}
		else
		{
			add(x,y,a[y]);
			add(y,x,a[x]);  //Original graph
			add2(x,y,a[y]);
			add2(y,x,a[x]);  //Inverse graph
		}
	}
	spfa(1);spfa2(n);ans=0;  //spfa: running maximum and minimum
	for(int i=2;i<n;i++)
	ans=max(ans,maxn[i]-minn[i]); //Maximum difference
	cout<<ans;
	
	return 0;
}