Now I understand how rubbish the shortest problem I've ever done is.

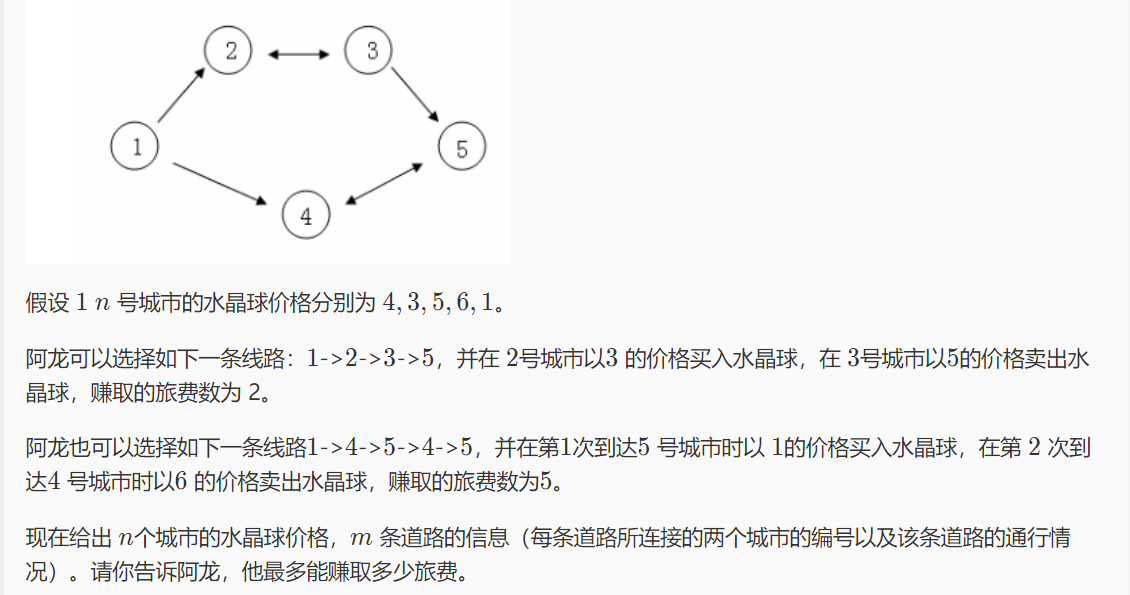
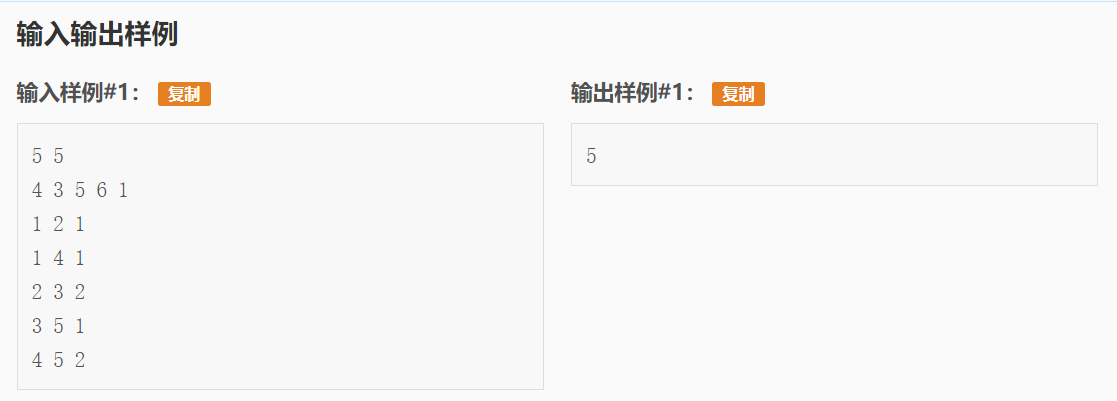
It's a long topic, but in fact, it's a story about a middleman making a difference. Generally speaking, the problem of graph theory is the core of graph construction, and the subtlety of this problem lies in that it needs to build two graphs: positive graph and reverse graph. Positive graph is the path of 1-n, while reverse graph is from n to 1.

The topic requires us to buy in a certain city, and then sell in a certain city. We can maintain two values. The maximum price for selling is mx and the minimum price mi. For cities that can reach each other, the minimum value and the maximum value are the same.

So first run spfa from 1-n to find the minimum value of the purchased goods, and then run spfa from n-1 on the inverse graph to find the maximum value of the sold goods when they come back. Last for all points, find the maximum difference.

In fact, it's very simple to think about it. The code is as follows (refer to Jiang Shen's code and online explanation):

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+7;
const int INF=0x3f3f3f3f;
struct node{
    int nxt;
    int to;
}edge[maxn*2];
struct node1{
    int nxt;
    int to;
}edge1[maxn*2];
int x,y,z;
int n,m; 
int head[maxn],cnt;
int val[maxn];
int mi[maxn],mx[maxn];
bool vis[maxn];
void add(int x,int y){
    edge[++cnt].nxt=head[x];
    edge[cnt].to=y;
    head[x]=cnt;
}
int head2[maxn],cnt2;
void add2(int x,int y){
    edge1[++cnt2].nxt=head2[x];
    edge1[cnt2].to=y;
    head2[x]=cnt2;
}
queue<int> q;
void spfa1(){
    for(int i=1;i<=n;i++){
        mi[i]=INF;
        vis[i]=false;
    }
    mi[1]=val[1];
    q.push(1);
    vis[1]=true;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=edge[i].nxt){
            int v=edge[i].to;
            if(mi[v]>min(mi[u],val[v])){
                mi[v]=min(mi[u],val[v]);
                if(!vis[v]){
                    q.push(v);
                    vis[v]=true;
                }
            }
        }
    }
}
void spfa2(){
    for(int i=1;i<=n;i++){
        mx[i]=-INF;
        vis[i]=false;
    }
    mx[n]=val[n];
    q.push(n);
    vis[n]=true;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head2[u];i;i=edge1[i].nxt){
            int v=edge1[i].to;
            if(mx[v]<max(mx[u],val[v])){
                mx[v]=max(mx[u],val[v]);
                if(!vis[v]){
                    q.push(v);
                    vis[v]=true;
                }
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&val[i]);
    }
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&x,&y,&z);
        if(z==1){
            add(x,y);
            add2(y,x);
        } 
        else{
            add(x,y);
            add(y,x);
            add2(x,y);
            add2(y,x); 
        }
    }
    spfa1();
    spfa2();
    int ans=0;
    for(int i=1;i<=n;i++){
        ans=max(ans,mx[i]-mi[i]);
    } 
    printf("%d\n",ans);
    return 0;
}