Problem solving ideas:

First, let's analyze the operation of quary. We query an interval less than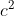For non whole blocks, the number of elements is just a violent query, but for the whole block, how can we know how many elements are less than  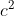And? Let's analyze here: if the whole block is disordered, we can only judge whether it meets the conditions one by one. Obviously, in such a large data, violence is impossible for you to pass; OK, let's think again. If this block is ordered, can we get the answer faster? Yes, we can use dichotomy after ordering. The efficiency of dichotomy is also very high. The positive solution is indeed dichotomy. In this case, quary will finish the analysis. Next, let's analyze the add operation. It's similar to the first question, except that there are more small channels for the quary function and a good vector container. What's the function? Of course, it's necessary to arrange a block in order.. (also, the lower_bound function in STL is much shorter than handwritten bisection.).. After we change the elements in the sequence, adding the same elements to the whole block at the same time will keep the relative size unchanged, that is, the sequence order has not changed; But for non whole blocks, it is equivalent to adding some elements in the whole block and keeping the other elements unchanged. At this time, the block becomes disordered. In order to facilitate quary, we need to reorder the block. So far, the add function has almost finished analyzing. After knowing the operations we want above, we need to preprocess, except for the same L[x],R[x],lazy[x],blong[i] as the first question, we need to put each element in the fast into the container and sort the elements already put into the container at the beginning.

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N=50010;
int n,m,L[N],R[N],block,num,blong[N];
ll a[N],lazy[N];
vector<ll> v[N];

void build()
{
    block=sqrt(n);//The size of each block has the lowest complexity when sqrt(n)
    if(n%block==0) num = n/block;
    else num = n/block + 1;  //The last block may not be enough
    for(int i=1;i<=n;i++)
    {
        blong[i]=(i-1)/block + 1;//The number of blocks starts from 1, So should not be written as i/block
        v[blong[i]].push_back(a[i]);
    }
    for(int i=1;i<=num;i++)
    {
        L[i]=(i-1)*block+1,R[i]=i*block;//Left and right boundaries of each block
    }
    R[num] = n; //The last piece of special treatment
    for(int i=1;i<=num;i++)
    {
        sort(v[i].begin(),v[i].end());
    }
}

void resort(int x)//Sort x blocks
{
    v[x].clear();
    for(int i=L[x];i<=R[x];i++)
    {
        v[x].push_back(a[i]);
    }
    sort(v[x].begin(),v[x].end());
}

void update(int l,int r,ll c)
{
    if(blong[l]==blong[r])
    {
        for(int i=l;i<=r;i++)
        {
            a[i]+=c;
        }
        resort(blong[l]);
        return;
    }
    for(int i=l;i<=R[blong[l]];i++)
    {
        a[i]+=c;
    }
    for(int i=blong[l]+1;i<=blong[r]-1;i++)
    {
        lazy[i]+=c;
    }
    for(int i=L[blong[r]];i<=r;i++)
    {
        a[i]+=c;
    }
    resort(blong[l]);
    resort(blong[r]);
}

int quary(int l,int r,ll c)
{
    int ans=0;
    if(blong[l]==blong[r])
    {
        for(int i=l;i<=r;i++)
        {
            if(a[i]+lazy[blong[i]]<c)
            ans++;
        }
        return ans;
    }
    for(int i=l;i<=R[blong[l]];i++)
    {
        if(a[i]+lazy[blong[i]]<c)
        ans++;
    }
    for(int i=blong[l]+1;i<=blong[r]-1;i++)
    {
        //We want to query the first position of a [i] + lazy [blong [i]] > = C (the vector subscript starts from zero)
        //After the item is moved, a[i] > = c-lazy [blong [i]]. Note that this a[i] (referring to the elements in the vector container) is not the same a[i] (referring to the original array)
        ans += lower_bound(v[i].begin(),v[i].end(),c-lazy[i])-v[i].begin();
    }
    for(int i=L[blong[r]];i<=r;i++)
    {
        if(a[i]+lazy[blong[i]]<c)
        ans++;
    }
    return ans;
}

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

inline ll Read(){
    ll  x=0;
    bool f=0;
    char ch=getchar();
    while (ch<'0'||'9'<ch)    f|=ch=='-', ch=getchar();
    while ('0'<=ch && ch<='9')
        x=x*10+ch-'0',ch=getchar();
    return f?-x:x;
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++) a[i]=Read();
    build();
    m=n;
    while(m--)
    {
        int op,l,r;
        ll c;
        op=read(),l=read(),r=read();c=Read();
        if(op==0) update(l,r,c);
        else printf("%d\n",quary(l,r,c*c));
    }
    return 0;
}