preface

We often use cache to improve data query speed. Due to the limited cache capacity, when the cache capacity reaches the upper limit, we need to delete some data to make room so that new data can be added. Cache data cannot be deleted randomly. Generally, we need to delete cache data according to some algorithm. Common elimination algorithms include LRU, LFU and FIFO. In this article, we talk about LRU algorithm.

Introduction to LRU

LRU is the abbreviation of Least Recently Used. This algorithm believes that the recently used data is hot data and will be used again next time. The data rarely used recently is unlikely to be used next time. When the cache capacity is full, the data rarely used recently will be eliminated first.
Suppose you cache internal data now, as shown in the figure:

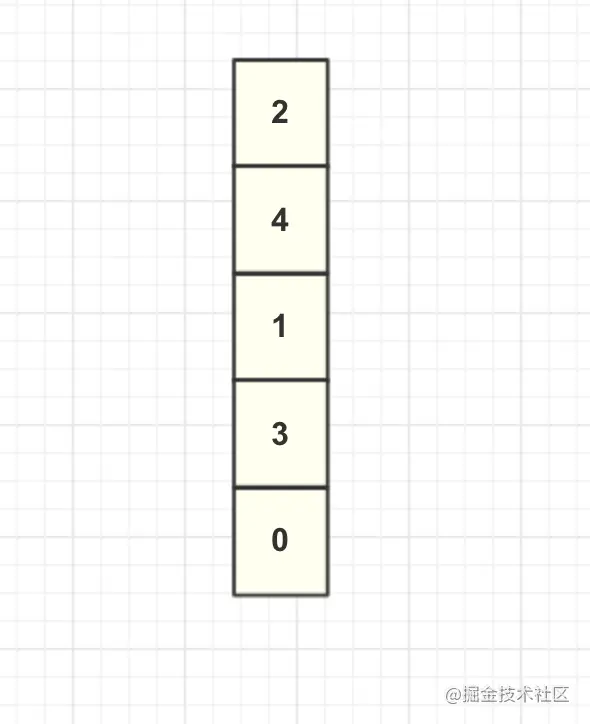
Here, we call the first node of the list as the head node and the last node as the tail node.

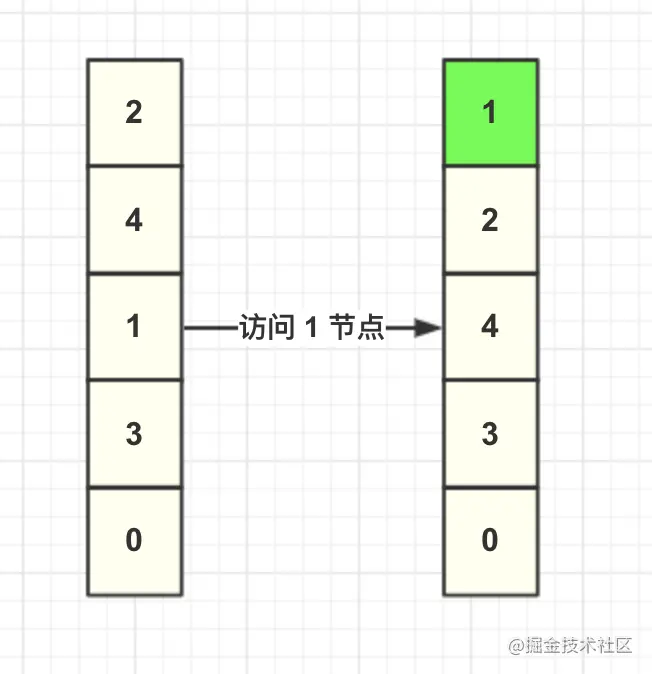
When calling the cache to obtain the data with key=1, the LRU algorithm needs to move the node 1 to the head node, and the other nodes remain unchanged, as shown in the figure.

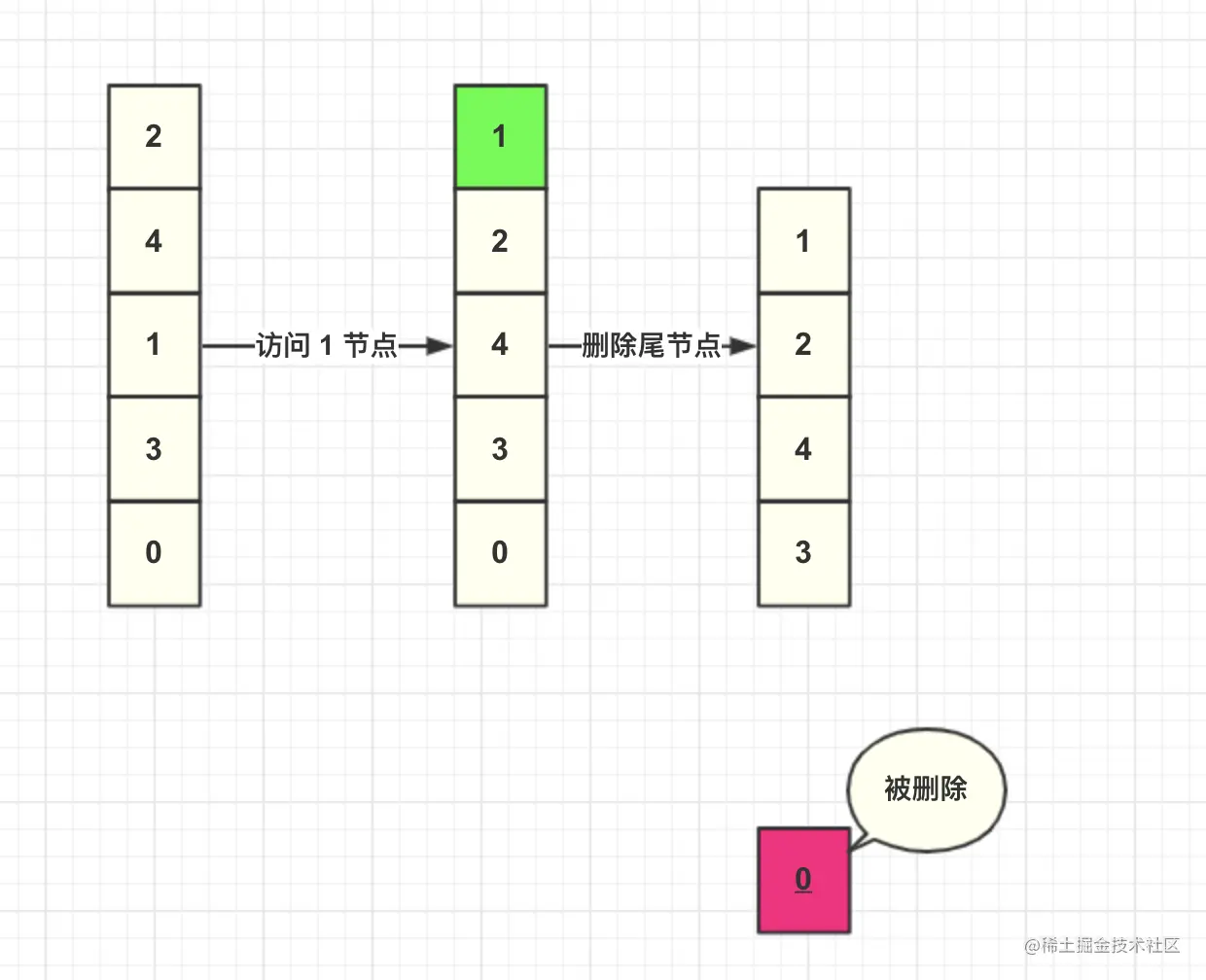
Then we insert a node with key=8. At this time, the cache capacity reaches the upper limit, so we need to delete the data before adding. Because each query will move the data to the head node, the non queried data will sink to the tail node, and the tail data can be considered as the least accessed data, so the data of the tail node is deleted.

Then we add the data directly to the head node.

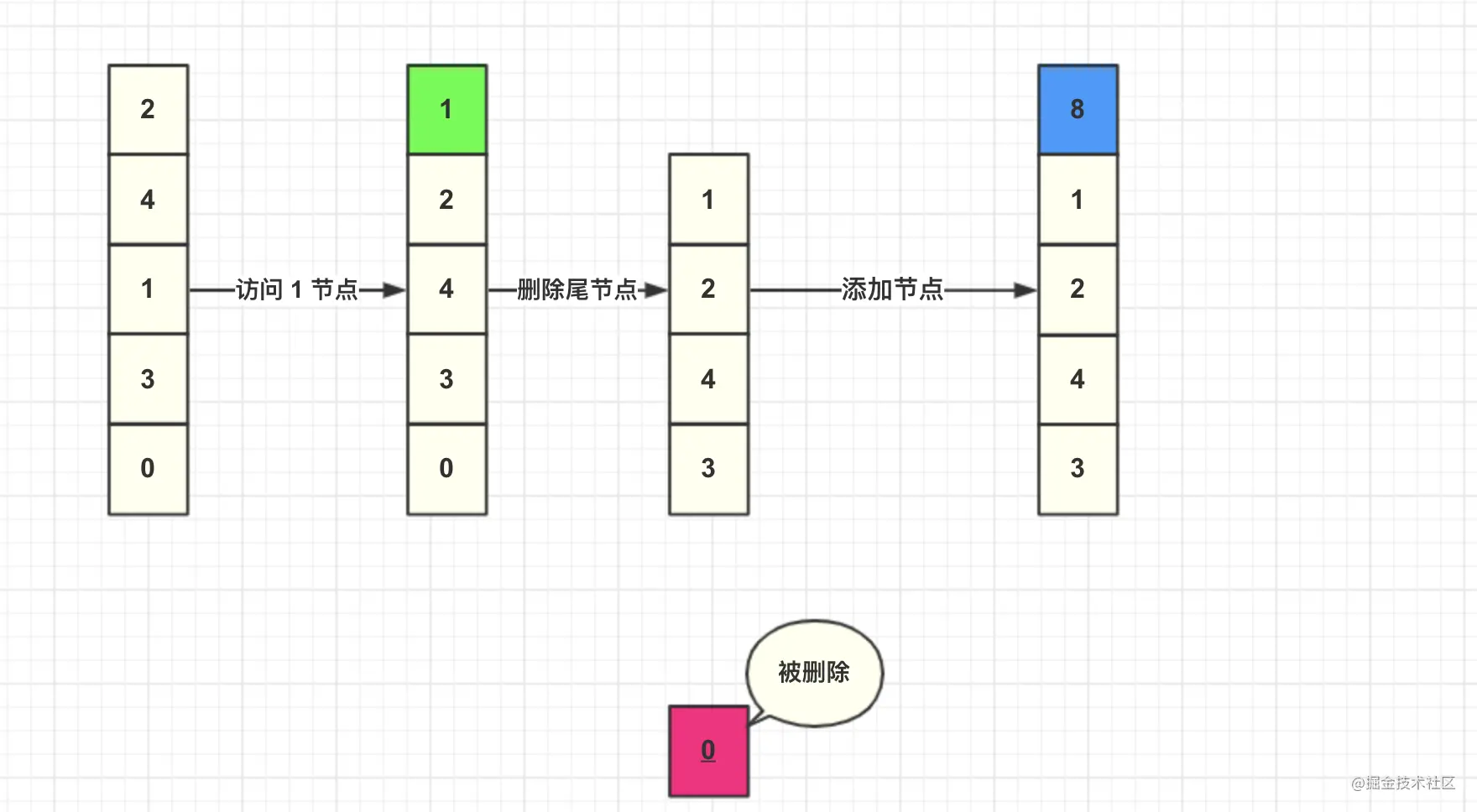
Here is a summary of the specific steps of LRU algorithm:

• New data is inserted directly into the list header
• Cache data hit, move data to the list header
• When the cache is full, remove the data at the end of the list.

Implementation of LRU algorithm

As can be seen from the above example, the LRU algorithm needs to add head nodes and delete tail nodes. The time complexity of adding / deleting nodes in the linked list is O(1), which is very suitable as a container for storing cached data. However, ordinary one-way linked lists cannot be used. One way linked lists have several disadvantages:

1. Every time any node data is obtained, it needs to traverse from the first node, which leads to the complexity of obtaining nodes as O(N).
2. To move the intermediate node to the head node, we need to know the information of the previous node of the intermediate node, and the one-way linked list has to traverse again to obtain the information.

The above problems can be solved in combination with other data structures.

Using hash table storage nodes, the complexity of obtaining nodes will be reduced to O(1). In the node mobility problem, the precursor pointer can be added to the node to record the information of the previous node, so that the linked list changes from a one-way linked list to a two-way linked list.

To sum up, the combination of two-way linked list and hash table is used, and the data structure is shown in the figure:

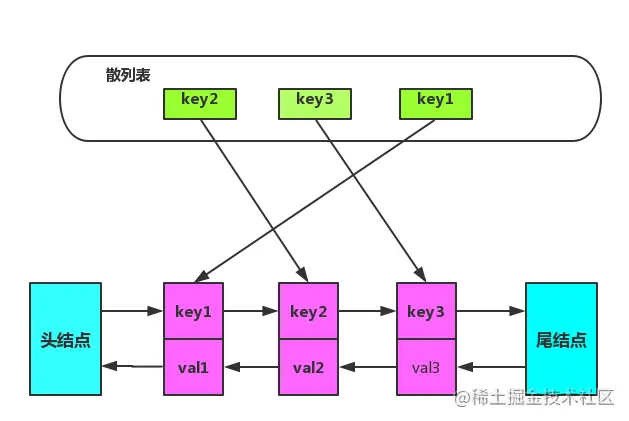
Two sentinel nodes are specially added to the two-way linked list to store any data. When using sentinel nodes, the absence of boundary nodes can be ignored when adding / deleting nodes, which simplifies the programming difficulty and reduces the code complexity.

The implementation code of LRU algorithm is as follows. In order to simplify key, val considers int type.

public class LRUCache {

    Entry head, tail;
    int capacity;
    int size;
    Map<Integer, Entry> cache;


    public LRUCache(int capacity) {
        this.capacity = capacity;
        // Initialize linked list
        initLinkedList();
        size = 0;
        cache = new HashMap<>(capacity + 2);
    }

    /**
     * If the node does not exist, return - 1. If it exists, move the node to the head node and return the data of the node.
     *
     * @param key
     * @return
     */
    public int get(int key) {
        Entry node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // There are mobile nodes
        moveToHead(node);
        return node.value;
    }

    /**
     * Add the node to the head node. If the capacity is full, the tail node will be deleted
     *
     * @param key
     * @param value
     */
    public void put(int key, int value) {
        Entry node = cache.get(key);
        if (node != null) {
            node.value = value;
            moveToHead(node);
            return;
        }
        // non-existent. Add it first and then remove the tail node
        // At this time, the capacity is full. Delete the tail node
        if (size == capacity) {
            Entry lastNode = tail.pre;
            deleteNode(lastNode);
            cache.remove(lastNode.key);
            size--;
        }
        // Add header node

        Entry newNode = new Entry();
        newNode.key = key;
        newNode.value = value;
        addNode(newNode);
        cache.put(key, newNode);
        size++;

    }

    private void moveToHead(Entry node) {
        // First delete the relationship of the original node
        deleteNode(node);
        addNode(node);
    }

    private void addNode(Entry node) {
        head.next.pre = node;
        node.next = head.next;

        node.pre = head;
        head.next = node;
    }

    private void deleteNode(Entry node) {
        node.pre.next = node.next;
        node.next.pre = node.pre;
    }


    public static class Entry {
        public Entry pre;
        public Entry next;
        public int key;
        public int value;

        public Entry(int key, int value) {
            this.key = key;
            this.value = value;
        }

        public Entry() {
        }
    }

    private void initLinkedList() {
        head = new Entry();
        tail = new Entry();

        head.next = tail;
        tail.pre = head;

    }

    public static void main(String[] args) {

        LRUCache cache = new LRUCache(2);

        cache.put(1, 1);
        cache.put(2, 2);
        System.out.println(cache.get(1));
        cache.put(3, 3);
        System.out.println(cache.get(2));

    }
}

LRU algorithm analysis

The cache hit rate is a very important index of the cache system. If the cache hit rate of the cache system is too low, it will lead to the backflow of queries to the database and increase the pressure of the database.
Combined with the above analysis, the advantages and disadvantages of LRU algorithm are analyzed.
The advantage of LRU algorithm is that it is not difficult to implement the algorithm. For hot data, LRU efficiency will be very good.
The disadvantage of LRU algorithm is that for occasional batch operations, such as batch query of historical data, it is possible to replace the popular data in the cache with these historical data, resulting in cache pollution, reducing the cache hit rate and slowing down the normal data query.

LRU algorithm improvement scheme

The following solutions are derived from MySQL InnoDB LRU improved algorithm

Split the linked list into two parts: hot data area and cold data area, as shown in the figure.

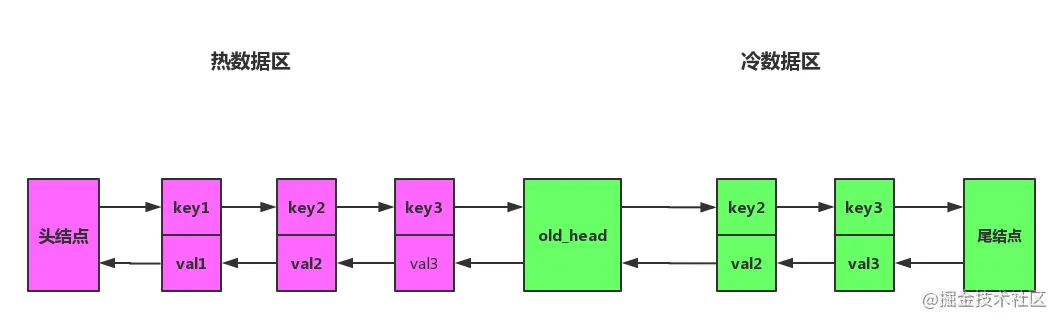
After improvement, the algorithm flow will become the following:

1. If the access data is located in the hot data area, it will be moved to the head node of the hot data area as in the previous LRU algorithm.
2. When inserting data, if the cache is full, eliminate the data of the tail node. Then insert the data into the head node of the cold data area.
3. Each time the data in the cold data area is accessed, the following judgment shall be made:
   • If the data has been in the cache for more than a specified time, such as 1 s, it will be moved to the head node of the hot data area.
   • If the data exists at a time less than the specified time, the location remains unchanged.

For occasional batch queries, the data will only fall into the cold data area and will soon be eliminated. The data in the hot data area will not be affected, which solves the problem of decreasing the cache hit rate of LRU algorithm.

Other improved methods include LRU-K, 2q and LIRs algorithms, which can be consulted by interested students.