Today we share with you the well-known LRU algorithm. The first lecture consists of four sections.

• Overview of LRU
• LRU usage
• LRU implementation
• Overview of Redis Near LRU

Part I: Overview of LRU

LRU is an abbreviation for Least Recently Used, translated as least recently used.Its rationale is that "recently used data will remain in use for some time to come, and the probable rate of data that has not been used for a long time will not be used for a long time to come", because this idea fits well with business scenariosAnd can solve many practical development problems, so we often use the idea of LRU to cache, commonly referred to as LRU cache mechanism.Because it happens to be on leetcode, I'll just post it here.But for LRU, I hope you are not confined to this topic (you don't have to worry about not learning, I hope to make the simplest version of the whole network, I hope you can keep it up!)Next, let's learn together.

Title: Design and implement an LRU (least recently used) cache mechanism using data structures that you have mastered.It should support getting the data get and writing the data put.

Example:

LRUCache cache = new LRUCache( 2 / Cache capacity / );

cache.put(1, 1);

cache.put(2, 2);

cache.get(1); // Return 1

cache.put(3, 3); // This operation will invalidate key 2

cache.get(2); // Return to -1 (not found)

cache.put(4, 4); // This operation will invalidate key 1

cache.get(1); // Return to -1 (not found)

cache.get(3); // Return 3

cache.get(4); // Return 4

Part 2: LRU usage

Let's start by explaining an example of LRUCache.

• Step 1: We declare an LRUCache of length 2
  
• Step 2: We put(1,1) and put(2,2) inside the cache, respectively, where 2 is first and 1 is last because 2 is recently used (put is also counted as use).

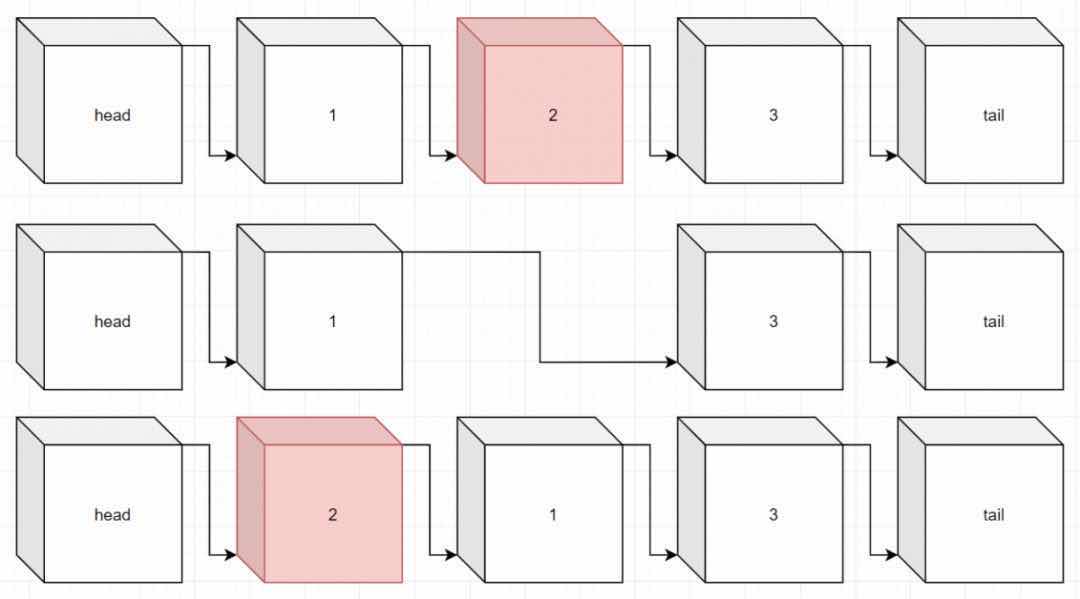
• Step 3: We get(1), which means we use 1, so we need to move 1 ahead.

• Step 4: At this point we put(3,3), because 2 is the least recently used, we need to scrape 2.If we get(2) again, we will return to -1.

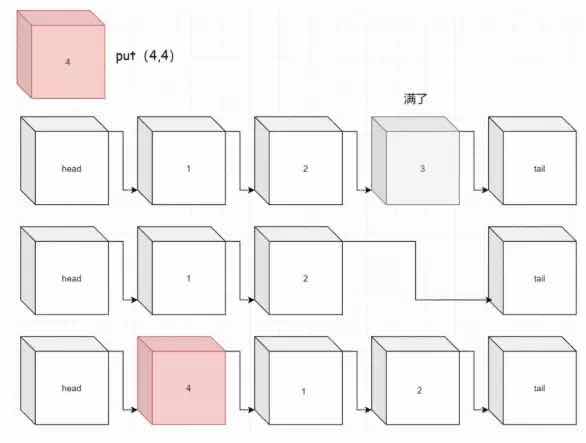
• Step 5: We will continue putting (4,4), similarly we will scrap 1.At this point, if get(1), it also returns -1.

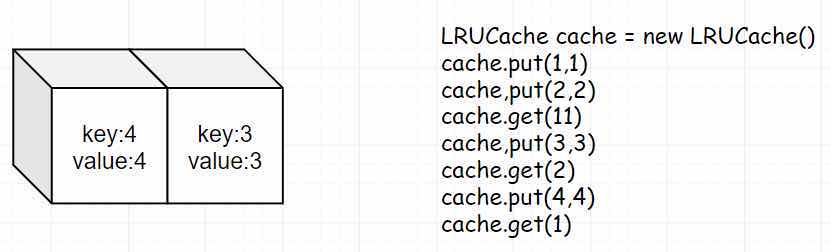
• Step 6: At this point we get(3), which actually adjusts the position of 3.

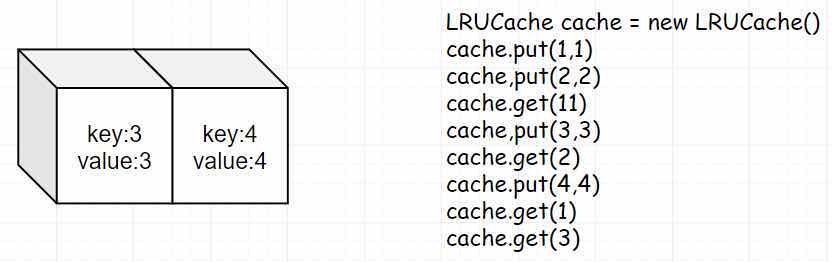
• Step 7: Same as get(4), continue to adjust position of 4.

Part Three: LRU Implementation (Layer by Layer)

First, we define a LinkNode to store elements.Because it's a two-way Chain table, naturally we want to define pre and next.At the same time, we need to store the key and value of the element below.val, you should all understand, the key is why you need to store the key?For example, when the entire cache is full, we need to delete the data in the map, query through the key in LinkNode, or we cannot get the key.

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

Now with LinkNode, you naturally need a Cache to store all Nodes.We define cap as the length of the cache, and m is used to store elements.head and tail are the beginning and end of the Cache.

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

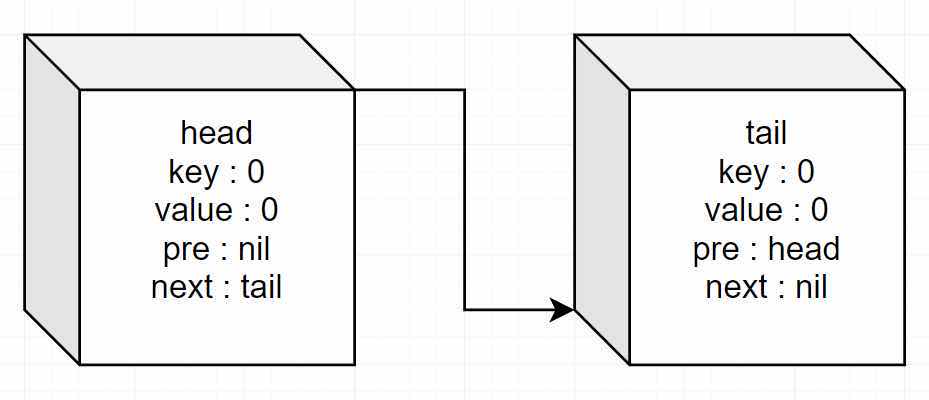
Next we initialize the entire Cache.Connect the head ers and tail s together when they are initialized.

func Constructor(capacity int) LRUCache {
    head := &LinkNode{0, 0, nil, nil}
    tail := &LinkNode{0, 0, nil, nil}
    head.next = tail
    tail.pre = head
    return LRUCache{make(map[int]*LinkNode), capacity, head, tail}
}

Probably this is:

Now that we have constructed the Cache, the rest is to add its API.Because Get is easy, let's finish the Get method first.There are two things to consider here. If no element is found, we return to -1.If an element exists, we need to move it to the top.

 func (this *LRUCache) Get(key int) int {
     head := this.head
     cache := this.m
     if v, exist := cache[key]; exist {
         v.pre.next = v.next
         v.next.pre = v.pre
         v.next = head.next
         head.next.pre = v
         v.pre = head
        head.next = v
        return v.val
    } else {
        return -1
    }
}

Probably like this (assuming 2 is the element of our get)

It's easy to think that this method will be used later, so pull it out.

func (this *LRUCache) moveToHead(node *LinkNode){
        head := this.head
        //Remove from current location
        node.pre.next = node.next
        node.next.pre = node.pre
        //Move to first position
        node.next = head.next
        head.next.pre = node
        node.pre = head
        head.next = node
}

func (this *LRUCache) Get(key int) int {
    cache := this.m
    if v, exist := cache[key]; exist {
        this.moveToHead(v)
        return v.val
    } else {
        return -1
    }
}

Now we're starting to finish Put.There are two scenarios to consider when implementing Put.If an element exists, it is actually equivalent to doing a Get operation and moving to the front (but note that there is an additional step to update the value).

func (this *LRUCache) Put(key int, value int) {
    head := this.head
    tail := this.tail
    cache := this.m
    //If the element exists
    if v, exist := cache[key]; exist {
        //1. Update Value
        v.val = value
        //2. Move to the front
        this.moveToHead(v)
    } else {
        //TODO
    }
}

If the element does not exist, we insert it at the beginning of the element and place the element value in the map.

func (this *LRUCache) Put(key int, value int) {
    head := this.head
    tail := this.tail
    cache := this.m
    //existence
    if v, exist := cache[key]; exist {
        //1. Update Value
        v.val = value
        //2. Move to the front
        this.moveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        v.next = head.next
        v.pre = head
        head.next.pre = v
        head.next = v
        cache[key] = v
    }
}

But we've missed a situation where the last element needs to be deleted if it happens to be full.Processing is complete, complete code for Put function is attached.

func (this *LRUCache) Put(key int, value int) {
    head := this.head
    tail := this.tail
    cache := this.m
    //existence
    if v, exist := cache[key]; exist {
        //1. Update Value
        v.val = value
        //2. Move to the front
        this.moveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        if len(cache) == this.cap {
            //Delete last element
            delete(cache, tail.pre.key)
            tail.pre.pre.next = tail
            tail.pre = tail.pre.pre
        }
        v.next = head.next
        v.pre = head
        head.next.pre = v
        head.next = v
        cache[key] = v
    }
}

Finally, let's finish all the code:

type LinkNode struct {
    key, val  int
    pre, next *LinkNode
}

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

func Constructor(capacity int) LRUCache {
    head := &LinkNode{0, 0, nil, nil}
    tail := &LinkNode{0, 0, nil, nil}
    head.next = tail
    tail.pre = head
    return LRUCache{make(map[int]*LinkNode), capacity, head, tail}
}

func (this *LRUCache) Get(key int) int {
    cache := this.m
    if v, exist := cache[key]; exist {
        this.moveToHead(v)
        return v.val
    } else {
        return -1
    }
}

func (this *LRUCache) moveToHead(node *LinkNode) {
    head := this.head
    //Remove from current location
    node.pre.next = node.next
    node.next.pre = node.pre
    //Move to first position
    node.next = head.next
    head.next.pre = node
    node.pre = head
    head.next = node
}

func (this *LRUCache) Put(key int, value int) {
    head := this.head
    tail := this.tail
    cache := this.m
    //existence
    if v, exist := cache[key]; exist {
        //1. Update Value
        v.val = value
        //2. Move to the front
        this.moveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        if len(cache) == this.cap {
            //Delete end element
            delete(cache, tail.pre.key)
            tail.pre.pre.next = tail
            tail.pre = tail.pre.pre
        }
        v.next = head.next
        v.pre = head
        head.next.pre = v
        head.next = v
        cache[key] = v
    }
}

After optimization:

type LinkNode struct {
    key, val  int
    pre, next *LinkNode
}

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

func Constructor(capacity int) LRUCache {
    head := &LinkNode{0, 0, nil, nil}
    tail := &LinkNode{0, 0, nil, nil}
    head.next = tail
    tail.pre = head
    return LRUCache{make(map[int]*LinkNode), capacity, head, tail}
}

func (this *LRUCache) Get(key int) int {
    cache := this.m
    if v, exist := cache[key]; exist {
        this.MoveToHead(v)
        return v.val
    } else {
        return -1
    }
}

func (this *LRUCache) RemoveNode(node *LinkNode) {
    node.pre.next = node.next
    node.next.pre = node.pre
}

func (this *LRUCache) AddNode(node *LinkNode) {
    head := this.head
    node.next = head.next
    head.next.pre = node
    node.pre = head
    head.next = node
}

func (this *LRUCache) MoveToHead(node *LinkNode) {
    this.RemoveNode(node)
    this.AddNode(node)
}

func (this *LRUCache) Put(key int, value int) {
    tail := this.tail
    cache := this.m
    if v, exist := cache[key]; exist {
        v.val = value
        this.MoveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        if len(cache) == this.cap {
            delete(cache, tail.pre.key)
            this.RemoveNode(tail.pre)
        }
        this.AddNode(v)
        cache[key] = v
    }
}

Because the algorithm is too important, give a Java version of the:

//java version
public class LRUCache {
  class LinkedNode {
    int key;
    int value;
    LinkedNode prev;
    LinkedNode next;
  }

  private void addNode(LinkedNode node) {
    node.prev = head;
    node.next = head.next;
    head.next.prev = node;
    head.next = node;
  }

  private void removeNode(LinkedNode node){
    LinkedNode prev = node.prev;
    LinkedNode next = node.next;
    prev.next = next;
    next.prev = prev;
  }

  private void moveToHead(LinkedNode node){
    removeNode(node);
    addNode(node);
  }

  private LinkedNode popTail() {
    LinkedNode res = tail.prev;
    removeNode(res);
    return res;
  }

  private Hashtable<Integer, LinkedNode> cache = new Hashtable<Integer, LinkedNode>();
  private int size;
  private int capacity;
  private LinkedNode head, tail;

  public LRUCache(int capacity) {
    this.size = 0;
    this.capacity = capacity;
    head = new LinkedNode();
    tail = new LinkedNode();
    head.next = tail;
    tail.prev = head;
  }

  public int get(int key) {
    LinkedNode node = cache.get(key);
    if (node == null) return -1;
    moveToHead(node);
    return node.value;
  }

  public void put(int key, int value) {
    LinkedNode node = cache.get(key);

    if(node == null) {
      LinkedNode newNode = new LinkedNode();
      newNode.key = key;
      newNode.value = value;
      cache.put(key, newNode);
      addNode(newNode);
      ++size;
      if(size > capacity) {
        LinkedNode tail = popTail();
        cache.remove(tail.key);
        --size;
      }
    } else {
      node.value = value;
      moveToHead(node);
    }
  }
}

Part 4: Introduction to Redis Near LRU

There is a parameter in Redis called "maxmemory-samples". Why?

# LRU and minimal TTL algorithms are not precise algorithms but approximated 
# algorithms (in order to save memory), so you can tune it for speed or 
# accuracy. For default Redis will check five keys and pick the one that was 
# used less recently, you can change the sample size using the following 
# configuration directive. 
# 
# The default of 5 produces good enough results. 10 Approximates very closely 
# true LRU but costs a bit more CPU. 3 is very fast but not very accurate. 
# 
maxmemory-samples 5

As we have said above, approximate LRU is a random sampling method to achieve an approximate LRU effect.This parameter is actually a way for the author to artificially interfere with the size of the sample, and the larger it is, the closer to the effect of the real LRU and, of course, the more memory it consumes.(The initial value of 5 is the author's default best)

This diagram illustrates that green points are new elements, dark gray points are elements that have not been deleted, and light gray points are deleted elements.The bottom one is a true LRU effect, and the second one is a default LRU effect of 5, so you can see if the light gray part fits the real one or not.The first figure shows the effect of setting this parameter to 10, which is close to that of a real LRU.

Because of the time relationship, this article is basically about this.How does the approximate LRU in Redis work?Please pay attention to the next issue~