brief introduction
dequeue refers to a two-way queue, which can insert and obtain data from the head of the queue or from the tail of the queue.
This article will introduce how to create dequeue and some basic operations of dequeue.
Implementation of bidirectional queue
Like ordinary queue items, bidirectional queues can be inserted and deleted at the head and tail respectively, so a dequeue needs to implement these four methods:
- insertFront(): inserts data from the dequeue header
- insertLast(): insert data from the end of dequeue
- deleteFront(): deletes data from the dequeue header
- deleteLast(): deletes data from the end of dequeue
Similarly, we also need a head and a rear to point to the head and tail nodes of the queue.
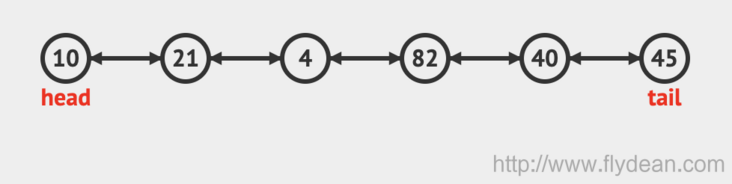
In other words, the queue that implements these four methods is a two-way queue. We don't care how it is implemented internally.
Next, let's intuitively experience the insertion and deletion of dequeue:
- Insert in head
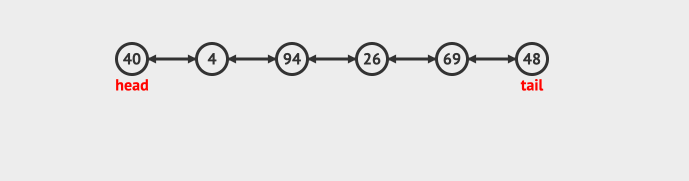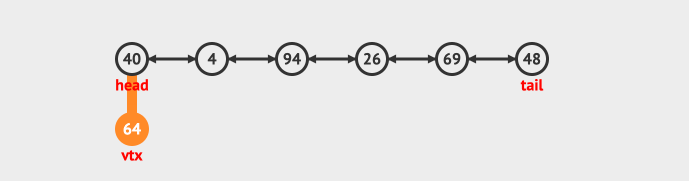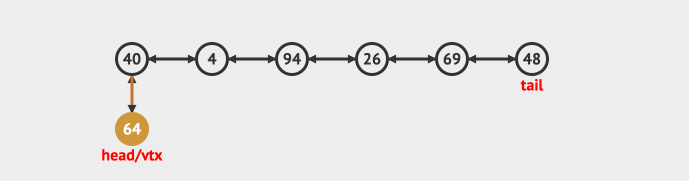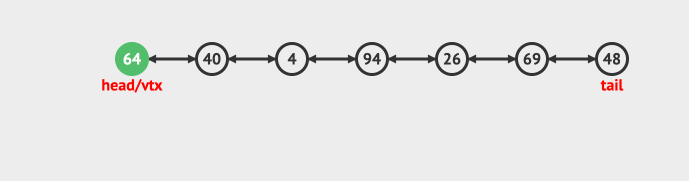
- Insert at tail
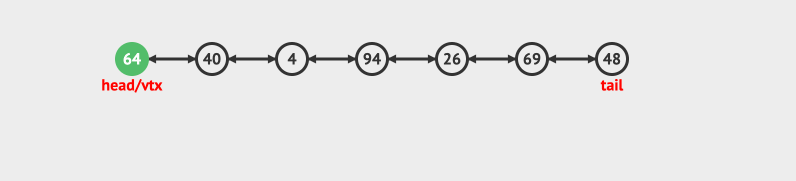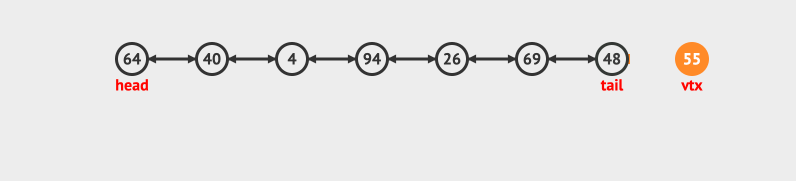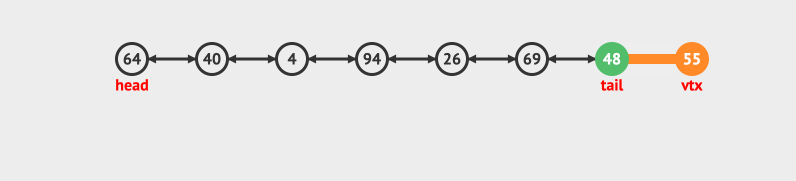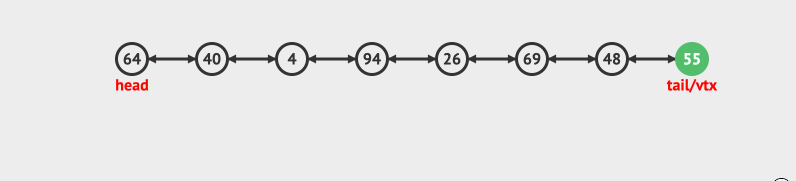
- Delete in header
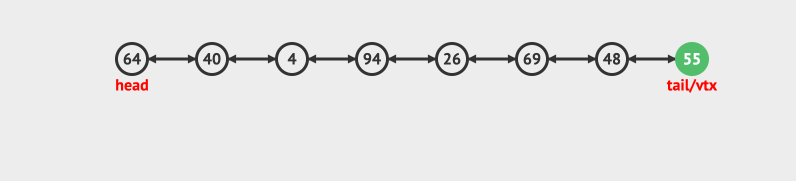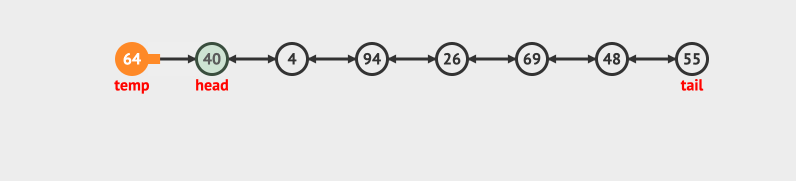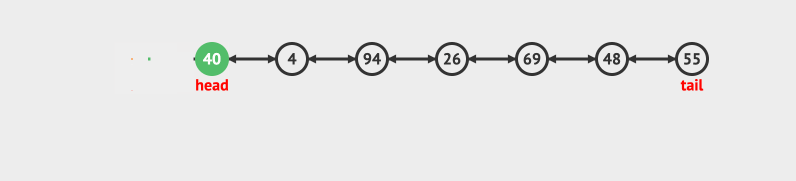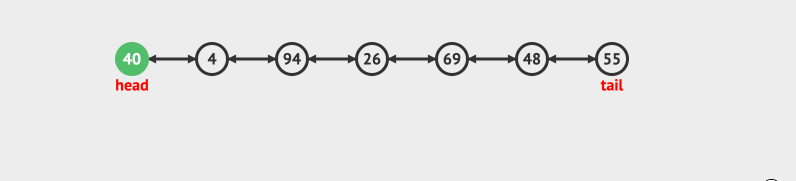
- Delete at tail

Bidirectional queues can also be implemented in many ways, such as circular arrays and linked lists.
Array implementation of bidirectional queue
Because the array itself has a context, that is, knowing that head can get the data behind it and knowing that rear can also get the data in front of it.
Therefore, in the implementation of array, it is enough to store the index values of head and rear.
We only need to add methods to insert data into the header and delete data from the tail:
//Head in queue
public void insertFront(int data){
if(isFull()){
System.out.println("Queue is full");
}else{
//Insert ArrayDeque from the head
head = (head + capacity - 1) % capacity;
array[head]= data;
//If the queue is empty before insertion, point real to head
if(rear == -1 ){
rear = head;
}
}
}
//Fetch data from tail
public int deleteLast(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data= array[rear];
//If there is only one element, reset head and real
if(head == rear){
head= -1;
rear = -1;
}else{
rear = (rear + capacity - 1)%capacity;
}
return data;
}
}Dynamic array implementation of bidirectional queue
Dynamic array can dynamically change the size of the array. Here we use multiplication to expand the array.
Let's see how to implement the extension method:
//Because it is a circular array, you can't make a simple array copy here
private void extendQueue(){
int newCapacity= capacity*2;
int[] newArray= new int[newCapacity];
//Copy all first
System.arraycopy(array,0,newArray,0,array.length);
//If rear < head, it means that the cycle has been carried out. You need to empty the data between 0-head and copy the data to the corresponding position of the new array
if(rear < head){
for(int i=0; i< head; i++){
//Reset data of 0-head
newArray[i]= -1;
//Copy to new location
newArray[i+capacity]=array[i];
}
//Reset the position of the rear
rear = rear +capacity;
//Reset capacity and array
capacity=newCapacity;
array=newArray;
}
}Because it is a circular array, we can't make a simple array copy here. We need to judge the position of rear and head to judge whether it enters the circular structure.
If the loop structure is entered, we need to reset the corresponding field data and copy it to the new array.
The methods of inserting data to the head and deleting data to the tail are consistent with the implementation of the basic queue, which is not listed here.
Linked list implementation of bidirectional queue
What is the problem if you use linked lists to implement two-way queues?
Insert at the head and insert at the tail can quickly locate the target node. But let's consider the tail deletion.
For tail deletion, we need to find the previous node of the tail node and set this node to the rear node. This requires that we can find its previous node through the rear node.
So the basic linked list can't meet our needs. Here we need to use a two-way linked list.
public class LinkedListDeQueue {
//head node
private Node headNode;
//Real node
private Node rearNode;
class Node {
int data;
Node next;
Node prev;
//Constructor for Node
Node(int d) {
data = d;
}
}
public boolean isEmpty(){
return headNode==null;
}
//Insert from the end of the team
public void insertLast(int data){
Node newNode= new Node(data);
//Point the next of the realnode to the newly inserted node
if(rearNode !=null){
rearNode.next=newNode;
newNode.prev=rearNode;
}
rearNode=newNode;
if(headNode == null){
headNode=newNode;
}
}
//Insert from the head of the team
public void insertFront(int data){
if(headNode == null){
headNode= new Node(data);
}else{
Node newNode= new Node(data);
newNode.next= headNode;
headNode.prev= newNode;
headNode= newNode;
}
}
//Delete from team leader
public int deleteFront(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data=headNode.data;
headNode=headNode.next;
headNode.prev=null;
}
return data;
}
//Delete from end of queue
public int deleteLast(){
int data;
if(isEmpty()){
System.out.println("Queue is empty");
return -1;
}else{
data=rearNode.data;
rearNode=rearNode.prev;
rearNode.next=null;
}
return data;
}
}Each node in the bidirectional linked list has two pointers: next and prev. Through these two pointers, we can quickly locate their next node and the previous node.
Time complexity of bidirectional linked list
Basically, the enQueue and deQueue methods implemented in the above three methods can immediately locate the location to enter or leave the queue, so their time complexity is O(1).
Code address of this article:
This article has been included in http://www.flydean.com/13-algorithm-dequeue/
The most popular interpretation, the most profound dry goods, the most concise tutorial, and many tips you don't know are waiting for you to find!
Welcome to my official account: "those things in procedure", understand technology, know you better!