Title Description
Ding Ding has recently become addicted to a digital game.The game seems simple, but after many days of research, Tintin finds that it is not easy to win under simple rules.The game is like this, there is a circle of integers (n in total) in front of you, you want to divide them into m parts in order, the numbers in each part are added together, the m results of the addition are modeled after 10, then multiplied, and finally you get a number k.The game requires that you get the maximum or minimum k.
For example, for the following circle of numbers (n=4, m=2):
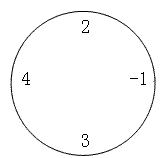
When minimum value is required, ((2-1) mod 10) ((4+3) mod 10)=1*7=7, when maximum value is required, ((2+4+3) mod 10) (-1 mod 10)=9*9=81.It is particularly noteworthy that the result of modelling 10 is non-negative whether negative or positive.
Tintin asked you to write a program to help him win the game.
Input and Output Formats
Input format:
The first line of the input file has two integers, n (1 < n < 50) and m (1 < m < 9).Each of the following n rows has an integer with an absolute value of no more than 104. The numbers in the circle are given in sequence, beginning and ending.
Output format:
The output file has two lines, each containing a non-negative integer.The first line is the minimum value your program gets, and the second line is the maximum value.
Input and Output Samples
4 2 4 3 -1 2
7 81
$DpMin[i][j][k]$represents the minimum of $k$times cut from $i$to $j$
$DpMax$for maximum
Enumerate breakpoints when transferring
Multiplication of left and right sides
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int MAXN=2001; const int INF=0x7fffff; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();} return x*f; } int DpMin[101][101][11]; int DpMax[101][101][11]; int a[MAXN]; int Query(int a) { return ((a%10)+10)%10; } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int n=read(),m=read(); for(int i=1;i<=n;i++) a[i]=read(),a[i+n]=a[i]; for(int i=1;i<=2*n;i++) a[i]+=a[i-1]; for(int l=1;l<=2*n;l++) for(int r=l;r<=2*n;r++) DpMin[l][r][1]=DpMax[l][r][1]=Query(a[r]-a[l-1]); for(int i=2;i<=m;i++) for(int l=1;l<=2*n;l++) for(int r=l+i-1;r<=2*n;r++) DpMin[l][r][i]=INF; for(int i=2;i<=m;i++)//Already cut k second for(int l=1;l<=2*n;l++) for(int r=l+i-1;r<=2*n;r++) for(int k=l+i-2;k<r;k++) { DpMin[l][r][i]=min(DpMin[l][r][i],DpMin[l][k][i-1]*Query(a[r]-a[k])); DpMax[l][r][i]=max(DpMax[l][r][i],DpMax[l][k][i-1]*Query(a[r]-a[k])); } int AnsMax=0,AnsMin=INF; for(int i=1;i<=n;i++) AnsMax=max(AnsMax,DpMax[i][i+n-1][m]), AnsMin=min(AnsMin,DpMin[i][i+n-1][m]); printf("%d\n%d",AnsMin,AnsMax); return 0; }