Background of problem
As we all know, for the search of elements in an ordered set, if the set is stored through an array, then the binary search algorithm can quickly find elements by using the efficiency of array random access. So suppose that if the collection is stored through a linked list, can it also realize the function of fast search?
Knowledge points
Linked list is also a kind of data structure. Unlike array, it does not need a piece of continuous memory space. Each element in the linked list maintains a pointer to the next element. Because each element only knows the next element, the search element must start from the header of the chain, traverse one by one until it finds the element or has reached the end of the linked list.
Features of linked list: slow query, fast insertion and deletion
Solutions
Imitating binary search idea, can linked list be used flexibly to realize fast search? Jump table data structure is to solve this problem.
For example, if you want to search the element 11 in a linked list, you have to search it 6 times before you can find it
The idea of binary search is to constantly narrow the search scope to find the specified elements. Then we can establish one or more levels of "index" at the upper level of the linked list, first determine the scope through the index, and then search the elements within the specified scope
Find element 11 by index here, as shown by the arrow, and the number of searches will be reduced. This is the realization of the skip table.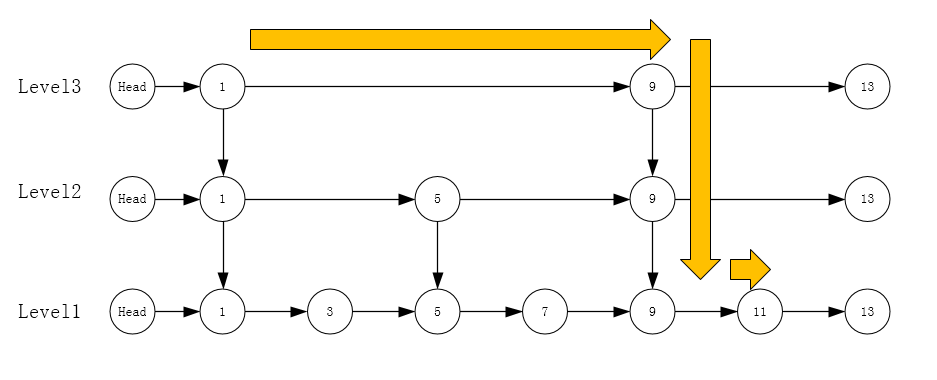
Special description
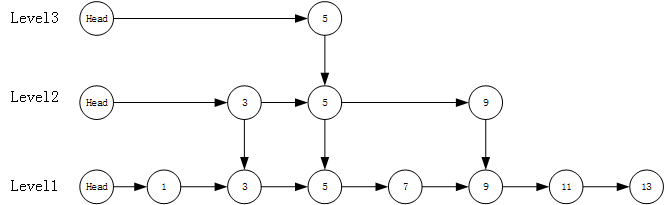
Which nodes will be indexed is not a regular process, but a random process. When inserting a node, several indexes can be created by calculating the random number of nodes.
For example, if the node calculates level=2, it will be indexed at level 1-2, and level=4, it will be indexed at level 1-4
So the skip table as shown in the figure above may be such an index, as shown in the following figure
Jump table implementation
Node definition
static final int MAX_LEVEL = 16; public class Node { // Node stored value private int data = -1; // If a node has indexes in multiple layers, the next level node pointer pointed by the node in each layer is maintained private Node forwards[] = new Node[MAX_LEVEL]; // Nodes are indexed at several levels private int maxLevel = 0; }
As shown in the above code, the node is abstracted into a high-level linked list node. Unlike the linked list node, the linked list node only maintains the pointer of the next node, while the current node maintains multiple pointers of the node at the corresponding level, as shown in the figure
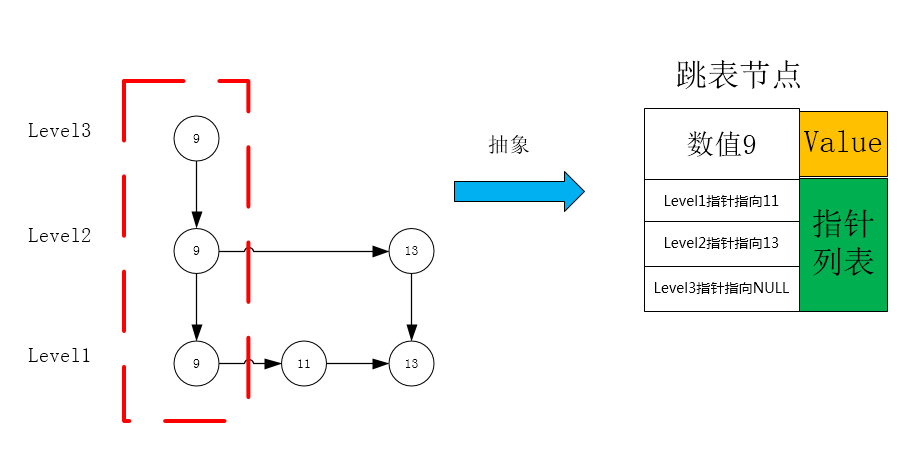
Node query
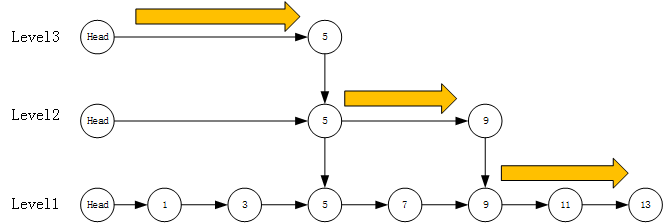
Start from the highest level (top level) to search for nodes, and find the largest node smaller than the search node. For example, in the following figure, find 13 nodes
- First, traverse from level 3, search to node 5, the value of node 5 is less than 13, and the subsequent nodes at Level 3 are empty
- Continue to sink to level 2, search node 9, the value of node 9 is less than 13, and subsequent nodes are empty at level 2
- Continue to sink to the lowest level 1, search to node 11, the subsequent nodes of node 11 are not empty but not less than node 13, temporarily take this node
- Judge whether the next level node value of the node in step 3 is equal to the search node. If yes, the next level node will be returned. Otherwise, null will be returned
Code implementation:
public Node find(int value) { Node p = head; // Start from the top layer and traverse the search to find the largest node smaller than the find node for (int i = levelCount - 1; i >= 0; --i) { while (p.forwards[i] != null && p.forwards[i].data < value) { p = p.forwards[i]; } } // If the next node of the largest node above is not the node to be searched, null will be returned; otherwise, this value will be returned if (p.forwards[0] != null && p.forwards[0].data == value) { return p.forwards[0]; } else { return null; } }
Node insertion
The idea of inserting elements is the same as that of single chain table. According to the above node query method, find the precursor and successor nodes of the elements to be inserted, and transform the nodes to be inserted to complete the insertion
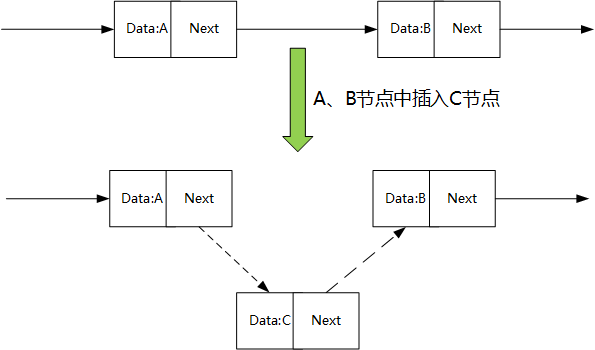
The difference is that the skip list maintains multi-level linked lists, so the above operations are also performed at multi-level
Code implementation:
// Limit the maximum number of levels private static final int MAX_LEVEL = 16; // Define number of levels private int levelCount = 1; // Define head node private Node head = new Node(); // Random number calculation private Random r = new Random() public void insert(int value) { // Using random number calculation method to randomly calculate the inserted value and establish several levels of index int level = randomLevel(); // New node Node newNode = new Node(); newNode.data = value; newNode.maxLevel = level; Node update[] = new Node[level]; for (int i = 0; i < level; ++i) { update[i] = head; } // Record the node with the maximum value less than the insertion value at each level. When inserting, the node pointer will point to the insertion value Node p = head; for (int i = level - 1; i >= 0; --i) { while (p.forwards[i] != null && p.forwards[i].data < value) { p = p.forwards[i]; } update[i] = p; } // The insertion node performs the pointer change operation similar to the insertion of linked list at each level for (int i = 0; i < level; ++i) { newNode.forwards[i] = update[i].forwards[i]; update[i].forwards[i] = newNode; } if (levelCount < level) levelCount = level; } private int randomLevel() { int level = 1; for (int i = 1; i < MAX_LEVEL; ++i) { if (r.nextInt() % 2 == 1) { level++; } } return level; }
The complete code of the whole hop table implementation
package skiplist; import java.util.Random; /** * An implementation method of skip table. * The skip table stores positive integers, and the stored ones are not repeated. * * */ public class SkipList { private static final int MAX_LEVEL = 16; private int levelCount = 1; private Node head = new Node(); // Lead list private Random r = new Random(); public Node find(int value) { Node p = head; for (int i = levelCount - 1; i >= 0; --i) { while (p.forwards[i] != null && p.forwards[i].data < value) { p = p.forwards[i]; } } if (p.forwards[0] != null && p.forwards[0].data == value) { return p.forwards[0]; } else { return null; } } public void insert(int value) { int level = randomLevel(); Node newNode = new Node(); newNode.data = value; newNode.maxLevel = level; Node update[] = new Node[level]; for (int i = 0; i < level; ++i) { update[i] = head; } // record every level largest value which smaller than insert value in update[] Node p = head; for (int i = level - 1; i >= 0; --i) { while (p.forwards[i] != null && p.forwards[i].data < value) { p = p.forwards[i]; } update[i] = p;// use update save node in search path } // in search path node next node become new node forwords(next) for (int i = 0; i < level; ++i) { newNode.forwards[i] = update[i].forwards[i]; update[i].forwards[i] = newNode; } // update node hight if (levelCount < level) levelCount = level; } public void delete(int value) { Node[] update = new Node[levelCount]; Node p = head; for (int i = levelCount - 1; i >= 0; --i) { while (p.forwards[i] != null && p.forwards[i].data < value) { p = p.forwards[i]; } update[i] = p; } if (p.forwards[0] != null && p.forwards[0].data == value) { for (int i = levelCount - 1; i >= 0; --i) { if (update[i].forwards[i] != null && update[i].forwards[i].data == value) { update[i].forwards[i] = update[i].forwards[i].forwards[i]; } } } } // Random level times, if it is odd number of layers + 1, prevent pseudo-random private int randomLevel() { int level = 1; for (int i = 1; i < MAX_LEVEL; ++i) { if (r.nextInt() % 2 == 1) { level++; } } return level; } public void printAll() { Node p = head; while (p.forwards[0] != null) { System.out.print(p.forwards[0] + " "); p = p.forwards[0]; } System.out.println(); } public class Node { // Node stored value private int data = -1; /** * If a node has indexes in multiple layers, the next level node pointer pointed by the node in each layer is maintained */ private Node forwards[] = new Node[MAX_LEVEL]; // Nodes are indexed at several levels private int maxLevel = 0; @Override public String toString() { StringBuilder builder = new StringBuilder(); builder.append("{ data: "); builder.append(data); builder.append("; levels: "); builder.append(maxLevel); builder.append(" }"); return builder.toString(); } } }
Application of skip table in Redis
Hop table is mainly used in the sort set data type in redis. We can see the source code implementation of hop table in redis
Preparatory knowledge points
redis source code is written in C language, with some special syntax briefly described
1. If the variable is preceded by *, it means that the variable is a pointer variable
2. If * is used before the function name, it means that the return value of the function is a pointer type data
3. struct structure, similar to class definition
4. Similar to zsl - > level = 1; zsl - > length = 0; represents the level and length attributes of the data pointed by the zsl pointer
The source code is based on Redis 3.2.11. After downloading and decompressing, check the source code in the src directory.
Definition of hop table node and hop table (server.h file)
// Define skip table node typedef struct zskiplistNode { //Node data robj *obj; // sort field double score; // Precursor pointer struct zskiplistNode *backward; struct zskiplistLevel { // Subsequent pointers are defined to maintain multiple pointers for each node of the array, and point to the corresponding next level at each level struct zskiplistNode *forward; unsigned int span; } level[]; } zskiplistNode; // Defining jump tables typedef struct zskiplist { struct zskiplistNode *header, *tail; // Number of nodes unsigned long length; // Layer progression int level; } zskiplist;
zskiplistNode defines the nodes in the hop table, including the following attributes:
- Data of robj *obj node
- The score of the score node can be understood as the sorting field (different nodes allow the same score, compare the data content under the same score, and compare the score preferentially under different scores. You can see the corresponding logic in the insertion source code below)
- The precursor pointer of a backward node. Generally, a linked list node maintains a successor pointer to the next node. Here, this pointer is the opposite concept, pointing to the previous node. From the definition point of view, the precursor pointer is not defined as an array, indicating that only the first level linked list is a two-way linked list
- zskiplistLevel is a structure, in which forward represents the subsequent pointer of the node, and the structure is defined as an array, indicating that each node will maintain multiple pointers, and each pointer points to the corresponding next level at each level. span represents how many nodes the current pointer spans. This count does not include the start node of the pointer, but the end node of the pointer. Used to calculate element rank
zskiplist defines the jump table data structure, which includes the following attributes:
- *header, *tail head pointer node and tail pointer node
- length represents the number of nodes in the linked list
- Level represents the level series of the jump table
Skip table related operations (t_zset.c file)
1. Jump table creation
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */ zskiplistNode *zslCreateNode(int level, double score, robj *obj) { zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel)); zn->score = score; zn->obj = obj; return zn; } zskiplist *zslCreate(void) { int j; zskiplist *zsl; zsl = zmalloc(sizeof(*zsl)); zsl->level = 1; zsl->length = 0; zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL); for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) { zsl->header->level[j].forward = NULL; zsl->header->level[j].span = 0; } zsl->header->backward = NULL; zsl->tail = NULL; return zsl; }
2. Skip table insertion
// Random calculation level int zslRandomLevel(void) { int level = 1; while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)) level += 1; return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL; } // Node insertion zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) { // update maintains the precursor node of the node to be inserted zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; unsigned int rank[ZSKIPLIST_MAXLEVEL]; int i, level; serverAssert(!isnan(score)); x = zsl->header; /** * Traverse from the top layer to find the largest node of all nodes smaller than the inserted node as the precursor node of the inserted node * The comparison node first compares the node contents with the same score */ for (i = zsl->level-1; i >= 0; i--) { rank[i] = i == (zsl->level-1) ? 0 : rank[i+1]; while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score && compareStringObjects(x->level[i].forward->obj,obj) < 0))) { rank[i] += x->level[i].span; x = x->level[i].forward; } update[i] = x; } // Determine the number of levels of nodes to be inserted for random calculation level = zslRandomLevel(); // Handle the assignment of the update of the predecessor node if the level of the inserted node is greater than the level of the existing skip table if (level > zsl->level) { for (i = zsl->level; i < level; i++) { rank[i] = 0; // There are no nodes in the new level, so the precursor node to be inserted is the head node update[i] = zsl->header; update[i]->level[i].span = zsl->length; } zsl->level = level; } // Create node x = zslCreateNode(level,score,obj); // Node inserts new elements similar to single chain table for (i = 0; i < level; i++) { x->level[i].forward = update[i]->level[i].forward; update[i]->level[i].forward = x; x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]); update[i]->level[i].span = (rank[0] - rank[i]) + 1; } for (i = level; i < zsl->level; i++) { update[i]->level[i].span++; } x->backward = (update[0] == zsl->header) ? NULL : update[0]; if (x->level[0].forward) x->level[0].forward->backward = x; else zsl->tail = x; zsl->length++; return x; }
Why is the data structure of the jump table used in redis instead of the red black tree?
-
Red black tree is more complex than skiplist in range lookup. On the red black tree, after we find the small value of the specified range, we need to continue to find other nodes that do not exceed the large value in the order of middle traversal. It is very simple to search the range on skiplist. Only after finding the small value, we need to traverse the first level list in several steps
-
The insertion and deletion of the red black tree may lead to the adjustment of the subtree, and the logic is complex. The insertion and deletion of the skiplist only need to modify the pointers of the adjacent nodes, so the operation is simple and fast
-
In terms of memory usage, skiplist is more flexible than balanced tree

