5. Linear table
Linear table is the most basic, simplest and most commonly used data structure. A linear table is a finite sequence of n data elements with the same characteristics

Precursor element: if element A is in front of element B, A is called the precursor element of B
Successor element: if element B is after element a, it is called the successor element of A
Characteristics of linear table: there is a "one-to-one" logical relationship between data elements.
-
The first data element has no precursor. This data element is called a header node
-
The last data element has no successor. This data element is called the tail node
-
In addition to the first and last data elements, other data elements have and have only one precursor and one successor
If the linear table is defined in mathematical language, it can be expressed as (a1,... ai-1,ai,ai+1,... an), ai-1 is ahead of ai, ai is ahead of ai+1,
ai-1 is the precursor element of ai, and ai+1 is the successor element of ai

Classification of linear table: the data in linear table can be stored in sequence or chain. According to different data storage methods, linear table can be divided into sequential table and chain table
5.1 sequence table
The sequential table is a linear table saved in the form of an array in the computer memory. The sequential storage of the linear table refers to the sequential storage of each element in the linear table with a group of storage units with continuous addresses, so that in the logical structure of the linear table, the adjacent data elements are stored in the adjacent physical storage units, That is, the logical adjacency relationship between data elements is reflected through the adjacency relationship physically stored by data elements
Physical storage and logical adjacency are the same

1) Implementation of sequence table
- API design
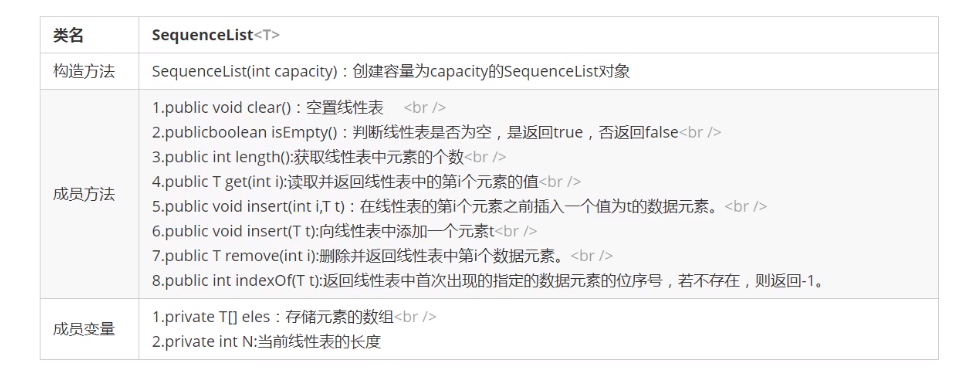
- code implementation
package chapter03;
/**
* @author Soil flavor
* Date 2021/9/3
* @version 1.0
* Sequence table
*/
public class SequenceList<T> {
/**
* An array of storage elements
*/
private T[] eles;
/**
* Record the number of elements in the current sequence table
*/
private int n;
/**
* Capacity of the current sequential table
*/
private int capacity;
/**
* Construct an array with capacity
*
* @param capacity
*/
public SequenceList(int capacity) {
this.eles = (T[]) new Object[capacity];
this.n = 0;
this.capacity = capacity;
}
/**
* Empty table
*/
public void clear() {
n = 0;
}
/**
* Judge whether the table is empty
*
* @return
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Get the length of the table: the number of elements in the table
*
* @return
*/
public int length() {
return n;
}
/**
* Returns the element at i position in the table
*
* @param i
* @return
*/
public T get(int i) {
if (i < 0 || i >= n) {
throw new RuntimeException("No index is" + i + "Element of");
}
return eles[i];
}
/**
* Insert the element t into the table at index i
*
* @param i
* @param t
*/
public void insert(int i, T t) {
// Judge whether the table is full
if (n == capacity) {
throw new RuntimeException("Table full!");
}
// Judge whether i is legal
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal insertion position!");
}
// Move the elements after i back: move back from back to front in turn
for (int index = n; index > i; index--) {
eles[index] = eles[index - 1];
}
// Put t at i
eles[i] = t;
// Number of elements n plus 1
n++;
}
/**
* Inserts the element t to the end of the table
*
* @param t
*/
public void insert(T t) {
if (n == capacity) {
throw new RuntimeException("Table full!");
}
eles[n++] = t;
}
/**
* Delete the element with index i in the table
*
* @param i
* @return
*/
public T remove(int i) {
// Judge whether i is legal
if (i < 0 || i >= n) {
throw new RuntimeException("No index is" + i + "Element of");
}
// Record the element of the i position
T res = eles[i];
// Move the elements after i position forward in turn
for (int index = i; index < n - 1; index++) {
eles[index - 1] = eles[index];
}
// Number of elements minus 1
n--;
// Returns the deleted element
return res;
}
/**
* Index of the first occurrence of the query element t in the table
*
* @param t
* @return
*/
public int indexOf(T t) {
// Judge whether t is legal
if (t == null) {
throw new RuntimeException("Illegal element!");
}
// Traverse the array, such as matching, and return the index
for (int i = 0; i < n; i++) {
if (eles[i].equals(t)) {
return i;
}
}
// Not found after traversal, return - 1
return -1;
}
}
public class TestSequenceList {
@Test
public void test(){
SequenceList<String> sl = new SequenceList<>(5);
//Assert.assertEquals(3,sl.length());
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert(1,"James");
sl.insert("O'Neill");
//sl.insert("Yi Jianlian");
System.out.println(sl.get(2));
System.out.println(sl.remove(3));
sl.clear();
System.out.println(sl.length());
}
}
Kobe McGrady 0
2) Traversal of sequence table
Generally, when storing data as a container, you need to provide traversal mode to the outside, so you need to provide traversal mode to the sequence table.
In java, foreach loops are generally used to traverse collections. If you want your SequenceList to support foreach loops, you need to do the following:
-
Let SequenceList implement Iterable interface and rewrite iterator method;
-
Provide an internal class SIterator inside the SequenceList, implement the Iterator interface, and override hasNext method and next method;
code:
public class SequenceList<T> implements Iterable<T>{
// Omit other methods
/**
* Get iterator
* @return
*/
@Override
public Iterator<T> iterator() {
return new Siterator();
}
/**
* Inner class: iterator
*/
private class Siterator implements Iterator{
/**
* cursor
*/
private int cursor;
/**
* constructor
*/
public Siterator() {
this.cursor = 0;
}
/**
* Determine whether there is a next
* @return
*/
@Override
public boolean hasNext() {
return cursor<n;
}
/**
* Get the next element
* @return
*/
@Override
public T next() {
return eles[cursor++];
}
}
}
public void test(){
SequenceList<String> sl = new SequenceList<>(5);
//Assert.assertEquals(3,sl.length());
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert(1,"James");
sl.insert("O'Neill");
//sl.insert("Yi Jianlian");
// The underlying implementation of the enhanced for loop is the iterator, which is a simplified version of the iterator
for (String s : sl) {
System.out.println(s);
}
}
Yao Ming James Kobe McGrady O'Neill
3) The capacity of the sequence table is variable
When designing the sequence table, we should consider its capacity scalability
Considering the capacity scalability of the container is actually changing the size of the array storing data elements
-
When adding elements
You should check whether the size of the current array can accommodate new elements. If not, you need to create a new array with larger capacity. Here, create a new array storage element with twice the capacity of the original array
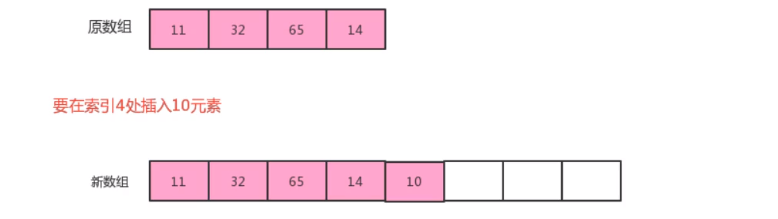
-
When removing elements
You should check whether the size of the current array is too large. For example, you are using an array with 100 capacity to store 10 elements, which will waste memory space. You should create an array with smaller capacity to store elements. If the number of data elements is found to be less than 1 / 4 of the capacity of the array, a new array storage element is created that is 1 / 2 of the capacity of the original array
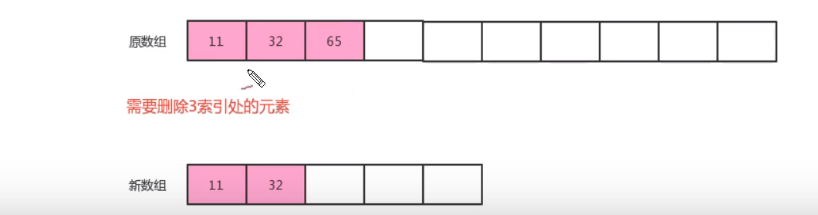
-
code implementation
public void insert(int i, T t) {
// Judge whether the table is full. If it is full, expand the capacity
if (n == capacity) {
//throw new RuntimeException("table full!");
resize(2 * capacity);
}
//....
}
public void insert(T t) {
// Judge whether the table is full. If it is full, expand the capacity
if (n == capacity) {
//throw new RuntimeException("table full!");
resize(2 * capacity);
}
eles[n++] = t;
}
public T remove(int i) {
// ....
// If the number of elements is less than 1 / 4 of the capacity, change the capacity to 1 / 2
if (n < capacity / 4) {
resize(capacity / 2);
}
// ....
}
/**
* Change sequence table capacity
*
* @param newCapacity
*/
private void resize(int newCapacity) {
// Record old array
T[] temp = eles;
// Create a new array
eles = (T[]) new Object[newCapacity];
// Copy old array elements to new array
for (int i = 0; i < n; i++) {
eles[i] = temp[i];
}
// Update array capacity value
capacity = newCapacity;
}
public class TestSequenceList {
@Test
public void test(){
SequenceList<String> sl = new SequenceList<>(3);
//Assert.assertEquals(3,sl.length());
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert(1,"James");
sl.insert("O'Neill");
sl.insert("Yi Jianlian");
for (String s : sl) {
System.out.println(s);
}
}
}
Yao Ming James Kobe McGrady O'Neill Yi Jianlian
4) Time complexity of sequence table
- get(i): no matter how large the number of data elements N is, the corresponding elements can be obtained only once eles[i], so the time complexity is O(1)
- Insert (int i, t, t): every time you insert, you need to move the elements behind I. as the number of elements N increases, the more elements you move, and the time complexity is O(n)
- remove(int i): every time you delete, you need to move the elements behind I. as the amount of data N increases, more elements will be moved, and the time complexity is O(n)
- Because the bottom layer of the sequence table is implemented by an array, and the length of the array is fixed, the container expansion operation is involved in the process of operation. In this way, the time complexity of the sequence table in the use process is not linear. At some nodes that need to be expanded, the time will increase sharply, especially the more elements, the more obvious the problem is
5) Implementation of ArrayList in java
The bottom layer of ArrayList set in java is also a sequence table, which is implemented by array. It also provides functions such as addition, deletion, modification, query and capacity expansion
5.2 linked list
1) Introduction
-
Disadvantages of sequence table
The sequential storage structure realizes the linear table. Although the query of the sequential table is very fast and the time complexity is O(1), the efficiency of addition and deletion is relatively low, because each addition and deletion operation is accompanied by the movement of a large number of data elements
Is there a solution to this problem? Yes, you can use another storage structure to realize linear list and chain storage structure
-
Linked list
It is a discontinuous and non sequential storage structure on the physical storage unit. Its physical structure can not intuitively represent the logical order of data elements,
The logical order of data elements is realized through the pointer link order in the linked list.The linked list consists of a series of nodes (each element in the linked list is called a node), which can be generated dynamically at run time
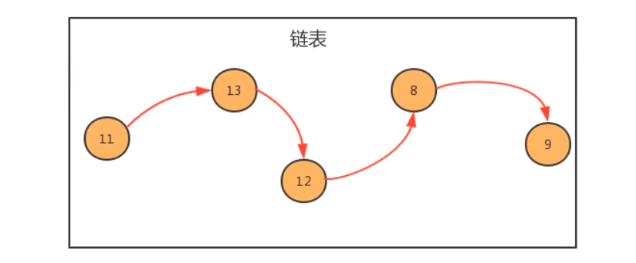
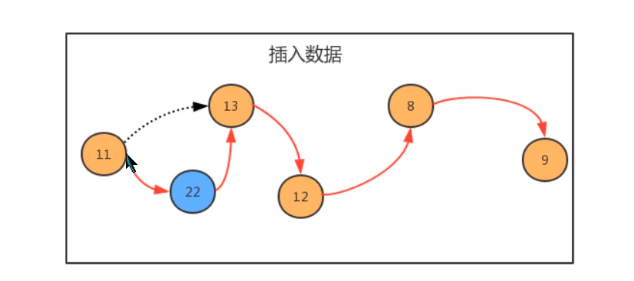
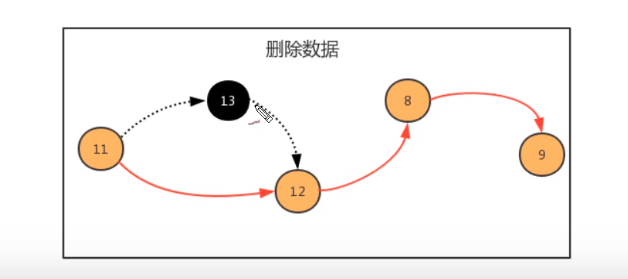
How do we use the linked list? According to the object-oriented idea, we can design a class to describe the node, use one attribute to describe the element stored in the node, and use another attribute to describe the next node of the node
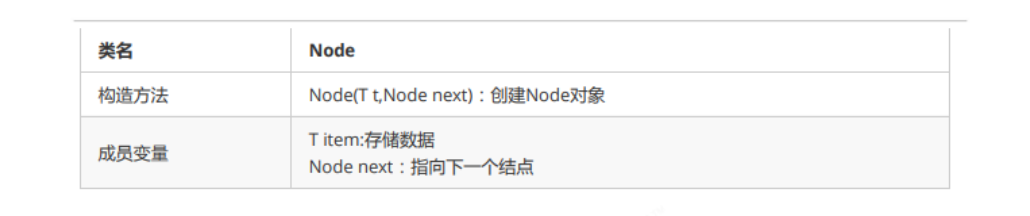
- Node class implementation
public class Node<T> {
/**
* Storage element
*/
public T item;
/**
* Point to the next node
*/
public Node next;
/**
* constructor
*
* @param item
* @param next
*/
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
- Generate linked list
public static void main(String[] args) {
Node<Integer> n1 = new Node<>(11, null);
Node<Integer> n2 = new Node<>(13, null);
Node<Integer> n3 = new Node<>(15, null);
Node<Integer> n4 = new Node<>(18, null);
Node<Integer> n5 = new Node<>(9, null);
Node<Integer> n6 = new Node<>(5, null);
n1.next = n2;
n2.next = n3;
n3.next = n4;
n4.next = n5;
n5.next = n6;
}
2) Unidirectional linked list
Unidirectional linked list is a kind of linked list. It is composed of multiple nodes. Each node is composed of a data field and a pointer field. The data field is used to store data and the pointer field is used to point to its subsequent nodes. The data field of the head node of the linked list does not store data, and the pointer field points to the first node that actually stores data

1. One way linked list API design
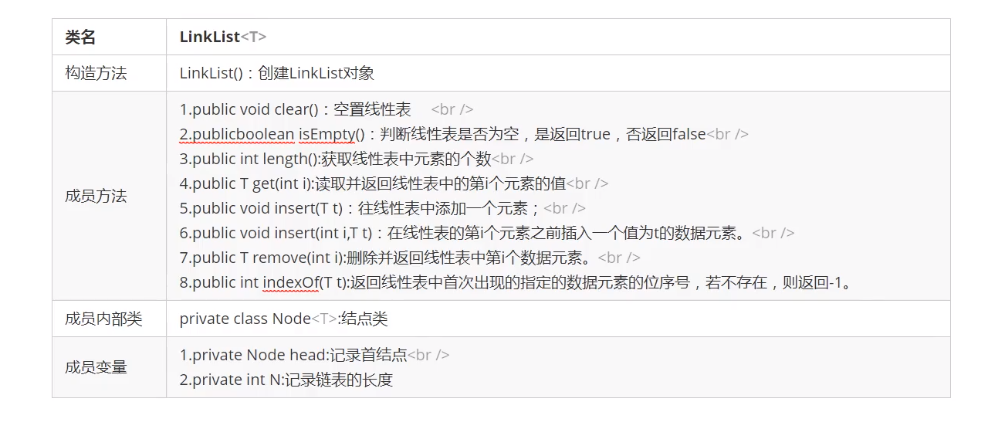
2. Code implementation
package chapter03;
import java.util.Iterator;
/**
* @author Soil flavor
* Date 2021/9/3
* @version 1.0
* Unidirectional linked list
*/
public class LinkList<T> implements Iterable<T> {
/**
* Head node
*/
private Node head;
/**
* Linked list length
*/
private int n;
/**
* constructor
*/
public LinkList() {
// Initialize header node
this.head = new Node(null, null);
this.n = 0;
}
/**
* Empty linked list
*/
public void clear() {
head.next = null;
n = 0;
}
/**
* Get linked list length
*
* @return
*/
public int length() {
return n;
}
/**
* Determine whether the linked list is empty
*
* @return
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Gets the element at i
*
* @param i
* @return
*/
public T get(int i) {
// Validity of test i
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal location!");
}
// Traverse the linked list and find i
Node node = head.next;
for (int index = 0; index < i; index++) {
node = node.next;
}
return node.item;
}
/**
* Add an element to the end of the linked list
*
* @param t
*/
public void insert(T t) {
// Find the last node
Node lastNode = head;
while (lastNode.next != null) {
lastNode = lastNode.next;
}
// Create a new node
Node newNode = new Node(t, null);
// Point the last node to the new node
lastNode.next = newNode;
// Number of links plus 1
n++;
}
/**
* Add an element to the linked list at i
*
* @param i
* @param t
*/
public void insert(int i, T t) {
// Test parameter validity
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal location!");
}
// Find the previous node at i
Node preNode = head;
for (int index = 0; index < i; index++) {
preNode = preNode.next;
}
// Get the node at i
Node node = preNode.next;
// Create a new node and point to the node at i
Node newNode = new Node(t, node);
// Point the previous node at i to the new node
preNode.next = newNode;
// Number of linked lists plus 1
n++;
}
/**
* Delete the element at i in the linked list
*
* @param i
* @return
*/
public T remove(int i) {
// Test parameter validity
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal location!");
}
// Find the previous node at i
Node preNode = head;
for (int index = 0; index < i; index++) {
preNode = preNode.next;
}
// Get the node at i
Node node = preNode.next;
// Point the node before i to the next node at i
preNode.next = node.next;
// List length minus 1
n--;
return node.item;
}
/**
* Gets the position where the element first appears in the linked list
*
* @param t
* @return
*/
public int indexOf(T t) {
// Traversal linked list
Node node = head;
// The cycle condition can be: n.next= null
for (int i = 0; i < n; i++) {
if (node.next.item.equals(t)) {
return i;
}
}
return -1;
}
/**
* Get iterator
*
* @return
*/
@Override
public Iterator<T> iterator() {
return new LIterator();
}
/**
* Inner class: iterator
*/
private class LIterator implements Iterator {
/**
* current node
*/
private Node node;
/**
* constructor
*/
public LIterator() {
this.node = head;
}
/**
* Judge whether the current node has a next node
* @return
*/
@Override
public boolean hasNext() {
return node.next != null;
}
/**
* Get the data of the next node
* @return
*/
@Override
public T next() {
// Set the next node as the current node
node = node.next;
return node.item;
}
}
/**
* Internal node class
*/
private class Node {
// Store data
T item;
// Next node
Node next;
/**
* constructor
*
* @param item
* @param next
*/
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
@Test
public void test(){
LinkList<String> sl = new LinkList<>();
//Assert.assertEquals(3,sl.length());
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert(1,"James");
sl.insert("O'Neill");
sl.insert("Yi Jianlian");
for (String s : sl) {
System.out.println(s);
}
System.out.println();
System.out.println(sl.get(2));
System.out.println(sl.remove(3));
sl.clear();
System.out.println(sl.length());
}
Yao Ming
James
Kobe
McGrady
O'Neill
Yi Jianlian
Kobe
McGrady
0
3) Bidirectional linked list
Bidirectional linked list, also known as bidirectional list, is a kind of linked list. It is composed of multiple nodes. Each node is composed of a data field and two pointer fields
The data field is used to store data. One pointer field is used to point to its successor node, and the other pointer field is used to point to the predecessor node
The data field of the head node of the linked list does not store data, the pointer field value pointing to the predecessor node is null, and the pointer field pointing to the successor node points to the first node that actually stores data

1. Node API design

2. Bi directional linked list API design
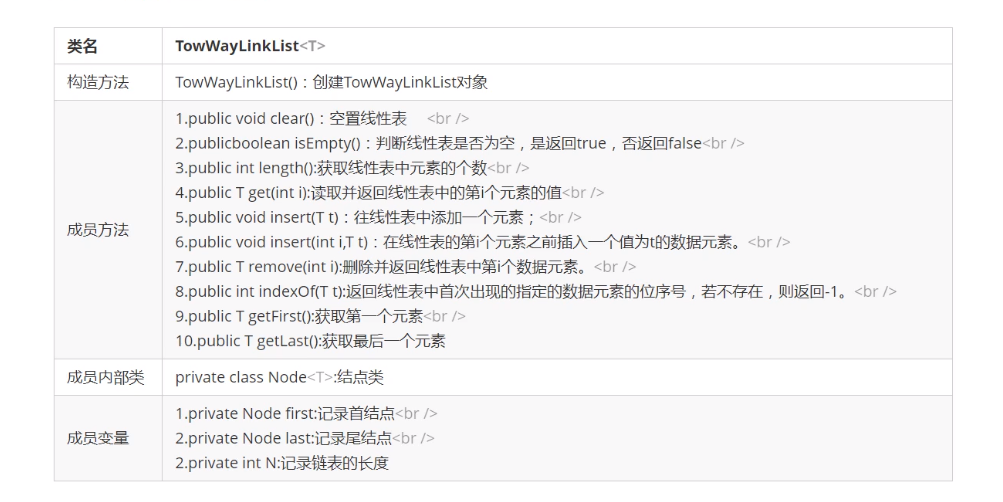
3. Code implementation
package chapter03;
import java.util.Iterator;
/**
* @author Soil flavor
* Date 2021/9/3
* @version 1.0
* Bidirectional linked list
*/
public class TwoWayLinkList<T> implements Iterable<T> {
/**
* Head node
*/
private Node head;
/**
* Tail node
*/
private Node last;
/**
* Linked list length
*/
private int n;
/**
* constructor
*/
public TwoWayLinkList() {
this.head = new Node(null, null, null);
this.last = null;
this.n = 0;
}
/**
* Empty table
*/
public void clear() {
head.pre = null;
head.item = null;
head.next = null;
last = null;
n = 0;
}
/**
* Determine whether the linked list is empty
*
* @return
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Get the length of the linked list
*
* @return
*/
public int length() {
return n;
}
/**
* Get i elements
*
* @param i
* @return
*/
public T get(int i) {
// Validity of test parameters
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal location!");
}
// ergodic
Node node = head.next;
for (int index = 0; index < i; index++) {
node = node.next;
}
return node.item;
}
/**
* Insert an element at the end of the linked list
*
* @param t
*/
public void insert(T t) {
if (isEmpty()) {
// The linked list is empty
// Create a new node
Node newNode = new Node(t, head, null);
// Make the new node the tail node
last = newNode;
// Let the head node point to the tail node
head.next = last;
} else {
// Linked list is not empty
Node oldLast = last;
// Create a new node
Node newNode = new Node(t, oldLast, null);
// Make the current tail node point to the new node
oldLast.next = newNode;
// Make the new node the tail node
last = newNode;
}
// Number of linked lists plus 1
n++;
}
/**
* Insert element t at i
*
* @param i
* @param t
*/
public void insert(int i, T t) {
// Test parameter validity
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal insertion position!");
}
// Find the previous node at position i
Node preNode = head;
for (int index = 0; index < i; index++) {
preNode = preNode.next;
}
// Get the node at i position
Node currentNode = preNode.next;
// Create a new node
Node newNode = new Node(t, preNode, currentNode);
// Modify the next pointer of the previous node at i position to a new node
preNode.next = newNode;
// Modify the pre pointer of the i position node to a new node
currentNode.pre = newNode;
// Number of links plus 1
n++;
}
/**
* Delete element at i
*
* @param i
* @return
*/
public T remove(int i) {
// Test parameter validity
if (i < 0 || i >= n) {
throw new RuntimeException("Illegal deletion location!");
}
// Find the previous node at position i
Node preNode = head;
for (int index = 0; index < i; index++) {
preNode = preNode.next;
}
// Find i location node
Node currentNode = preNode.next;
// Find the next node at i position; If currentNode is the last node, nextNode=null
Node nextNode = currentNode.next;
// Modify the next pointer of the previous node at i position to the next node at i position
preNode.next = nextNode;
// Modify the pre pointer of the next node at i position to the previous node at i position
if (i < n - 1) {
// Non tail node
nextNode.pre = preNode;
} else {
// Tail node
// nextNode is null and nextNode.pre is a null pointer
last = preNode;
}
// The number of linked lists minus 1
n--;
return currentNode.item;
}
/**
* Get the position where element t first appears
*
* @param t
* @return
*/
public int indexOf(T t) {
Node node = head;
for (int i = 0; i < n; i++) {
if (node.next.item.equals(t)) {
return i;
}
}
return -1;
}
/**
* Get the first element (non head node)
*
* @return
*/
public T getFirst() {
if (isEmpty()) {
return null;
}
return head.next.item;
}
/**
* Get end element
*
* @return
*/
public T getLast() {
if (isEmpty()) {
return null;
}
return last.item;
}
@Override
public Iterator<T> iterator() {
return new TIterator();
}
/**
* Internal node class
*/
private class Node {
/**
* Store data
*/
private T item;
/**
* Previous node
*/
private Node pre;
/**
* Next node
*/
private Node next;
/**
* constructor
*
* @param item
* @param pre
* @param next
*/
public Node(T item, Node pre, Node next) {
this.item = item;
this.pre = pre;
this.next = next;
}
}
/**
* Inner class: iterator
*/
private class TIterator implements Iterator {
/**
* current node
*/
private Node node;
/**
* constructor
*/
public TIterator() {
this.node = head;
}
/**
* Is there a next element
*
* @return
*/
@Override
public boolean hasNext() {
return node.next != null;
}
/**
* Get the next element
*
* @return
*/
@Override
public T next() {
node = node.next;
return node.item;
}
}
}
@Test
public void test2(){
TwoWayLinkList<String> sl = new TwoWayLinkList<>();
//Assert.assertEquals(3,sl.length());
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert(1,"James");
sl.insert("O'Neill");
sl.insert("Yi Jianlian");
for (String s : sl) {
System.out.println(s);
}
System.out.println();
System.out.println(sl.get(0));
System.out.println(sl.remove(0));
System.out.println();
System.out.println(sl.getFirst());
System.out.println(sl.getLast());
sl.clear();
System.out.println(sl.length());
}
Yao Ming James Kobe McGrady O'Neill Yi Jianlian Yao Ming Yao Ming James Yi Jianlian 0
4. Implementation of LinkedList in java
The LinkedList set in java is also implemented using a two-way linked list, and provides related methods such as addition, deletion, modification and query
3) Linked list complexity analysis
-
get(int i): each query needs to start from the head of the linked list and look back in turn. As the number of data elements N increases, more elements are compared. The time complexity is O(n)
-
Insert (int i, t, t): for each insertion, you need to find the previous element at position I first, and then complete the insertion operation. With the increase of data element N, the more elements to find, and the time complexity is O(n)
-
remove(int i): for each removal, you need to find the previous element at position I first, and then complete the insertion operation. As the number of data elements N increases, the more elements are found, and the time complexity is O(n)
Compared with the sequential list, the insertion and deletion time complexity of the linked list is the same, but it still has great advantages, because the physical address of the linked list is discontinuous, the storage space size does not need to be specified in advance, does not involve operations such as capacity expansion, and does not involve the exchange of elements
Compared with the sequential list, the query performance of the linked list will be lower. Therefore, if there are many query operations in the program, it is recommended to use sequential list, and there are many addition and deletion operations, it is recommended to use linked list
4) Linked list inversion
The reversal of single linked list is a high-frequency topic in the interview
- Requirement: the data in the original linked list is: 1 - > 2 - > 3 > 4. After inversion, the data in the linked list is: 4 - > 3 - > 2 - > 1
- Reverse API:

-
principle
Using recursion can complete the inversion. In fact, recursive inversion starts from the first node of the original linked list to store data, and recursively calls to reverse each node in turn until the last node is reversed, and the whole linked list is reversed
Inversion is to modify the point of the node pointer
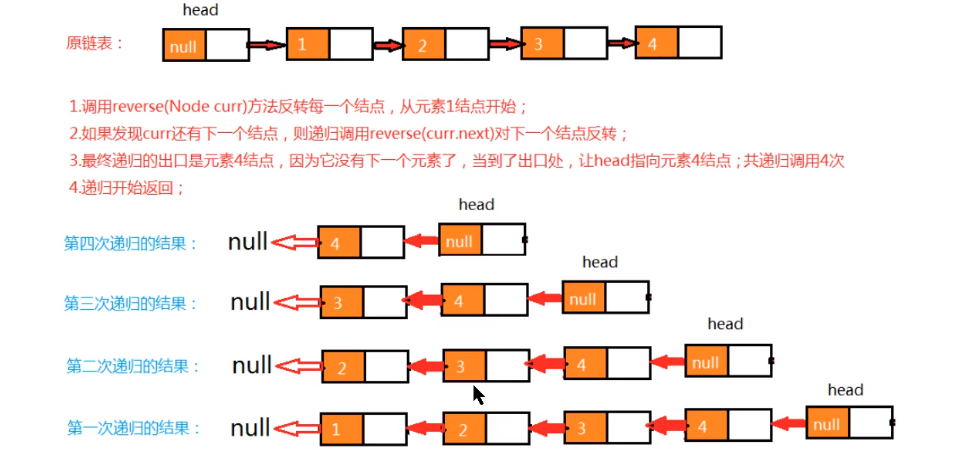
- code implementation
/**
* Linked list inversion
*/
public void reverse() {
// If the element is empty or there is only one element, there is no need to reverse
if (n < 2) {
return;
}
// Call overloaded method inversion
reverse(head.next);
}
/**
* Invert the current node
*
* @param curr
* @return Reverse curr and return
*/
private Node reverse(Node curr) {
// If it is a tail node, point the head node to the tail node and return
if (curr.next == null) {
// The head node points to the tail node
head.next = curr;
return curr;
}
//The previous node of the current node
Node pre = reverse(curr.next);
pre.next = curr;
//The next node of the current node is set to null
curr.next = null;
//Returns the current node
return curr;
}
@Test
public void test3(){
LinkList<String> sl = new LinkList<>();
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
//sl.insert("James");
//sl.insert("O'Neill");
//sl.insert("Yi Jianlian");
for (String s : sl) {
System.out.println(s);
}
System.out.println("----------------");
sl.reverse();
for (String s : sl) {
System.out.println(s);
}
}
Yao Ming Kobe McGrady ---------------- McGrady Kobe Yao Ming
Use the debug debugging mode in Idea, cooperate with F7 and F8, carefully analyze the operation process, and run it several times
5) Speed pointer
Speed pointer refers to defining two pointers. The movement speed of the two pointers is fast and slow, so as to create the desired difference. This difference can let us find the corresponding node on the linked list. In general, the moving step of the fast pointer is twice that of the slow pointer
1. Intermediate value problem
-
principle
Using the speed pointer, a linked list is regarded as a runway. Assuming that the speed of a is twice that of b, then when a runs the full range, b just runs half, so as to find the intermediate node
As shown in the following figure, at first, the slow and fast pointers point to the first node of the linked list, then slow moves one pointer at a time, and fast moves two pointers at a time
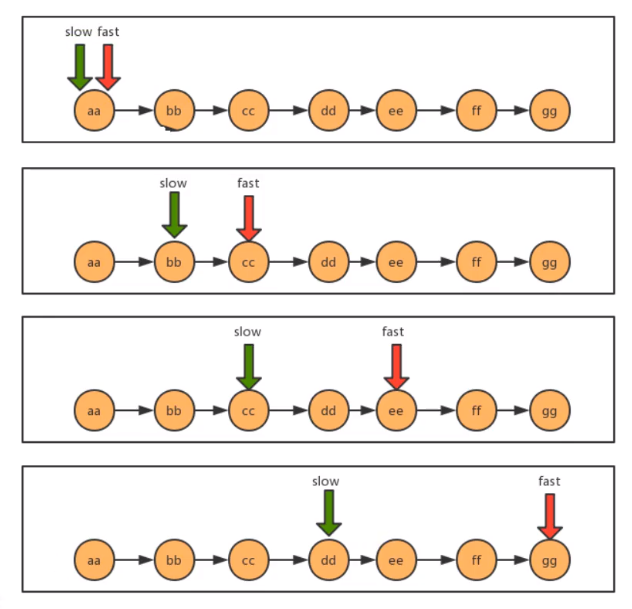
- code implementation
/**
* Find intermediate nodes with fast and slow pointers
* @return
*/
public T getMid(){
// Define speed pointers: both point to the first element node
Node fast = head.next;
Node slow = head.next;
// Traverse the linked list: when the fast pointer reaches the end of the linked list, it ends
while(fast!=null && fast.next!=null){
// Go two steps at a time
fast = fast.next.next;
// The slow pointer takes one step at a time
slow = slow.next;
}
return slow.item;
}
@Test
public void testGetMid(){
LinkList<String> sl = new LinkList<>();
sl.insert("Yao Ming");
sl.insert("Kobe");
sl.insert("McGrady");
sl.insert("James");
sl.insert("O'Neill");
//sl.insert("Yi Jianlian");
for (String s : sl) {
System.out.println(s);
}
System.out.println("-----------");
System.out.println(sl.getMid());
}
Yao Ming Kobe McGrady James O'Neill ----------- McGrady
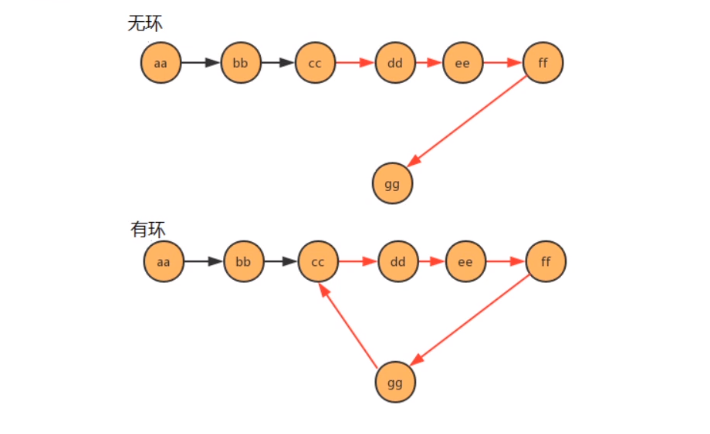
2. Is there a ring problem with the one-way linked list
-
principle
Using the idea of speed pointer, compare the linked list to a runway. If there are rings in the linked list, then this runway is a circular runway. In a circular runway, two people have a speed difference, so sooner or later, two people will meet. As long as they meet, it means there are rings
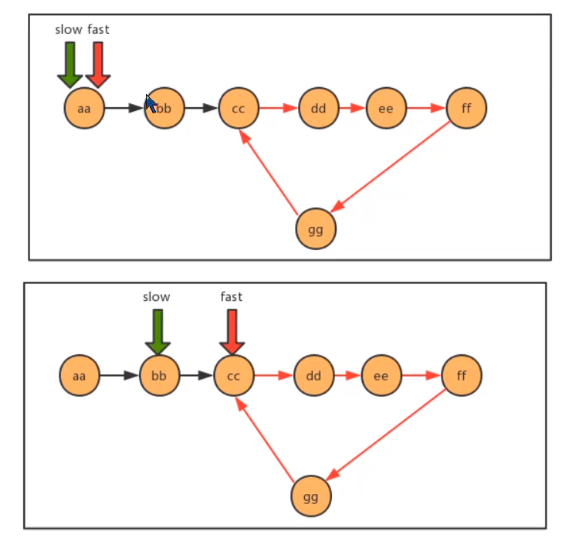
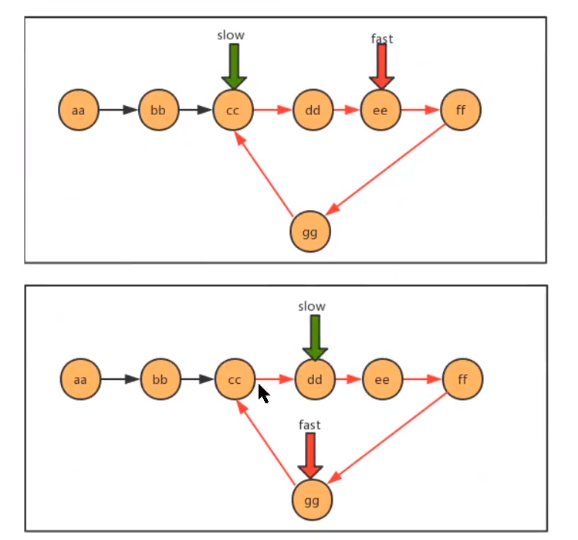
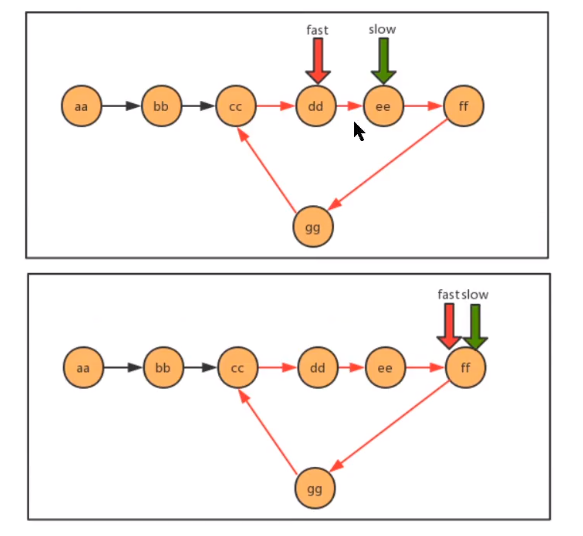
- code implementation
/**
* Determine whether there are links in the linked list
* @param first First node of linked list
* @return ture Is ring, false is acyclic
*/
public static boolean isCircle(Node<String> first) {
Node<String> slow = first;
Node<String> fast = first;
// If there is a loop, fast will never be null, and there must be exit judgment conditions in the loop
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if (fast.equals(slow)){
return true;
}
}
return false;
}
Another way to judge whether a one-way linked list has a ring:
Traverse the linked list. If the number of traversals exceeds the number of elements in the linked list, it is a ring; If the number of traversals is equal to the number of elements and can exit, it is acyclic; In this way, you only need to traverse one cycle; When the fast and slow pointer has a ring, the traversal times will exceed one cycle, because after the fast pointer reaches one cycle, it will have to catch up with the slow pointer to end
3. Linked list entry problem
-
principle
When the fast and slow pointers meet, it can be judged that there is a ring in the linked list. At this time, reset a new pointer to the starting point of the linked list, and the step size is 1 as the slow pointer. Then the place where the slow pointer meets the "new" pointer is the entrance of the ring
Proving this conclusion involves the knowledge of number theory, which is omitted here and only about realization
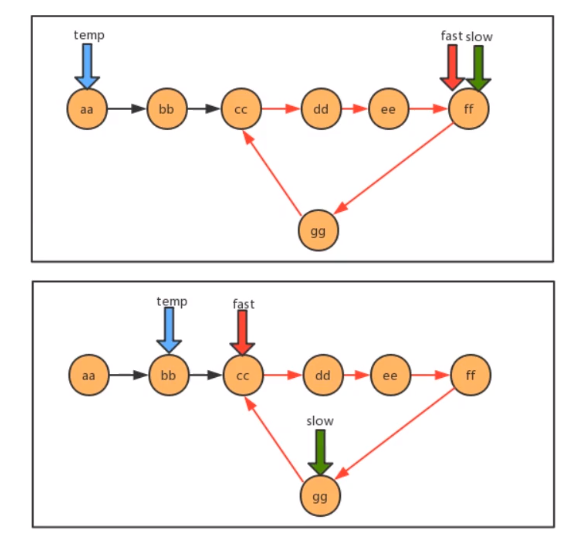
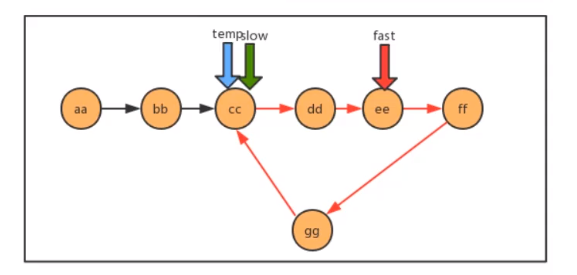
6) Circular linked list
Circular linked list, as the name suggests, the whole linked list should form a circular ring. In a one-way linked list, the pointer of the last node is null and does not point to any node, because there is no next element. To realize the circular linked list, you only need to make the pointer of the last node of the one-way linked list point to the head node
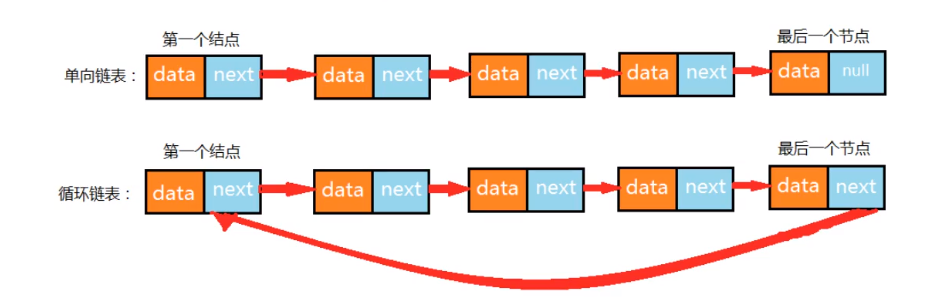
7) Joseph problem
-
Problem description
It is said that after the Romans occupied jotapat, 39 Jews hid in a cave with Joseph and his friends. 39 Jews decided to die rather than be caught by the enemy, so they decided to commit suicide. 41 people lined up in a circle. The first person counted off from 1, and then, if someone counted off to 3, Then this person must commit suicide, and then his next person starts counting again from 1 until everyone commits suicide. However, Joseph and his friends did not want to comply. So Joseph asked his friend to pretend to obey first. He arranged his friend and himself in the 16th and 31st positions, so as to escape the death game
-
Problem conversion
41 people sit in a circle. The first person is numbered 1, the second person is numbered 2, and the nth person is numbered n
-
The person with number 1 starts to count back from 1, and the person with number 3 exits the circle
-
The next person starting from the person who quit will count off from 1 again, and so on
-
Find the number of the last person to quit
-
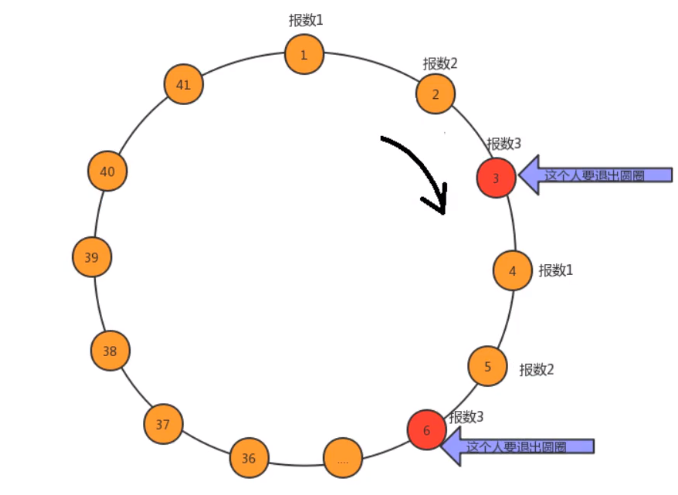
-
Problem solving ideas
-
A one-way circular linked list with 41 nodes is constructed, and the values of 1 ~ 41 are stored respectively to represent the 41 people
-
Use the counter count to record the value of the current number of messages
-
Traverse the linked list once per cycle, count++
-
Judge the value of count. If it is 3, delete the node from the linked list, print the value of the node, and reset the count to 0
-
-
code implementation
package chapter03;
import org.junit.Test;
/**
* @author Soil flavor
* Date 2021/9/4
* @version 1.0
* josephus problem
*/
public class JosephTest<T> {
@Test
public void test() {
// 1. A one-way circular linked list with 41 nodes is constructed, and the values of 1 ~ 41 are stored respectively to represent the 41 people
// Record first node
Node<Integer> first = null;
// Record previous node
Node<Integer> pre = null;
// Circular construction linked list
for (int i = 1; i < 42; i++) {
// First node
if (i < 2) {
first = new Node<>(i, null);
pre = first;
// Jump out of this cycle
continue;
}
// Intermediate node
Node<Integer> node = new Node<>(i, null);
pre.next = node;
pre = node;
// Tail node
if (i > 40) {
node.next = first;
}
}
// 2. Use the counter count to record the value of the current number of messages
int count = 0;
// 3. Traverse the linked list once per cycle, count++
// current node
Node<Integer> n = first;
// The previous node of the current node
Node<Integer> before = null;
while (n != n.next) {
// Analog alarm
count++;
// Judge whether the count is 3
if (count == 3) {
// Equal to 3, delete the current node, print the current node, reset count, and move the current node back
// Delete current node: directly use the previous node to point to the next node
before.next = n.next;
System.out.print(n.item + ",");
// Reset count
count = 0;
// Move current node backward
n = n.next;
} else {
// Not equal to 3, the current node moves back
// Move the previous node backward and record it as the current node
before = n;
// Move current node backward
n = n.next;
}
}
// Print last element
System.out.print(n.item);
}
/**
* Internal node class
*/
private class Node<T> {
/**
* Store data
*/
private T item;
/**
* Next node
*/
private Node next;
/**
* constructor
*
* @param item
* @param next
*/
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
3,6,9,12,15,18,21,24,27,30,33,36,39,1,5,10,14,19,23,28,32,37,41,7,13,20,26,34,40,8,17,29,38,11,25,2,22,4,35,16,31
5.3 stack
1) Stack concept
-
Stack in life
The place where goods are stored or passengers stay can be extended to warehouse and transfer station. For example, hotels in modern life were called inns in ancient times. They are places for passengers to rest. Passengers can enter the inn to rest and leave the inn after rest
-
Stack in computer
- We introduce the concept of stack in life into the computer, which is a place for data to rest. It is a data structure. Data can enter and exit the stack
- Stack is a data structure based on first in last out (FILO). It is a special linear table that can only be inserted and deleted at one end. It stores data according to the principle of first in and last out. The first entered data is pressed into the bottom of the stack, and the last data is at the top of the stack. When data needs to be read, data will pop up from the top of the stack (the last data will be read out first)
- We call the action of data entering the stack as pressing the stack, and the action of data leaving the stack as bouncing the stack
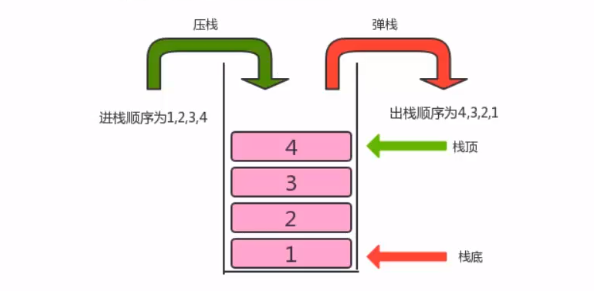
2) Implementation of stack
- API design
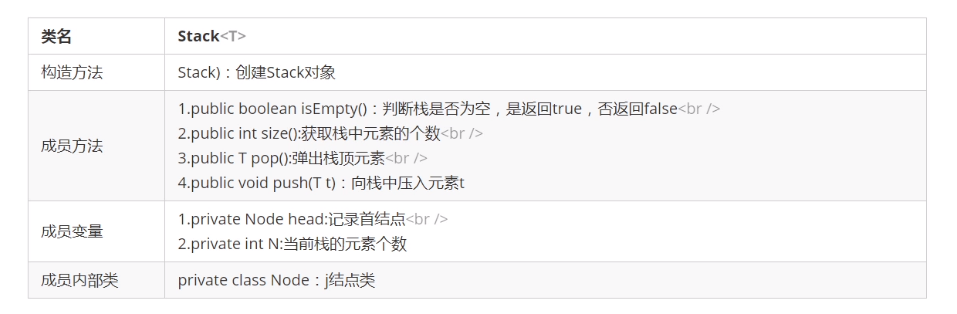
- code implementation
package chapter03;
import java.util.Iterator;
/**
* @author Soil flavor
* Date 2021/9/4
* @version 1.0
* Stack
*/
public class Stack<T> implements Iterable<T> {
/**
* First node
*/
private Node head;
/**
* Number of elements in stack
*/
private int n;
/**
* constructor
*/
public Stack() {
this.head = new Node(null, null);
this.n = 0;
}
/**
* Is the stack empty
*
* @return
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Number of elements in stack
*
* @return
*/
public int size() {
return n;
}
/**
* Stack pressing
*
* @param t
*/
public void push(T t) {
// Find the first node pointed to by the first node
Node oldFirst = head.next;
// Create a new node
Node newNode = new Node(t, null);
// Point the first node to the new node
head.next = newNode;
// Point the new node to the original first node
newNode.next = oldFirst;
// Number of elements plus 1
n++;
}
/**
* Bomb stack
*
* @return
*/
public T pop() {
// Find the first node pointed to by the first node
Node first = head.next;
// Point the first node to the second node: judge whether the first node exists
if (first != null) {
head.next = first.next;
// Number of elements minus 1
n--;
// Returns the first element
return first.item;
}
// Empty stack, return null
return null;
}
/**
* iterator
*
* @return
*/
@Override
public Iterator<T> iterator() {
return new SIterator();
}
/**
* Inner class: iterator
* @param
*/
private class SIterator implements Iterator {
private Node node;
public SIterator() {
this.node = head;
}
@Override
public boolean hasNext() {
return node.next != null;
}
@Override
public T next() {
node = node.next;
return node.item;
}
}
/**
* Internal node class
*/
private class Node {
T item;
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
public class StackTest {
@Test
public void test(){
Stack<String> stack = new Stack<>();
stack.push("a");
stack.push("b");
stack.push("c");
stack.push("d");
for (String s : stack) {
System.out.println(s);
}
System.out.println("--------");
System.out.println("eject:"+stack.pop());
System.out.println("surplus:"+stack.size());
System.out.println("--------");
for (String s : stack) {
System.out.println(s);
}
}
}
d c b a -------- eject: d Remaining: 3 -------- c b a
3) Case
1. Bracket matching problem
A string may contain "()" parentheses and other characters. Write a program to check whether the parentheses in the string appear in pairs
For example:
"(Shanghai) (Chang'an)": correct match
"Shanghai (Chang'an)": correct match
"Shanghai (Chang'an (Beijing) (Shenzhen) Nanjing)": correct match
"Shanghai (Chang'an)": wrong match
"((Shanghai) Chang'an": wrong match
-
thinking
-
Create a stack to store the left parenthesis
-
Traverse the string from left to right to get each character
-
Judge whether the character is an open bracket. If so, put it into the stack for storage
-
Judge whether the character is a closing bracket. If not, continue the next cycle
-
If the character is a closing parenthesis, an element t pops up from the stack
-
Judge whether the element t is null. If not, it proves that there is a corresponding left parenthesis. If yes, it proves that there is no corresponding left parenthesis
-
After the loop ends, judge whether there are left left parentheses in the stack. If there are, they do not match. If not, they match
-
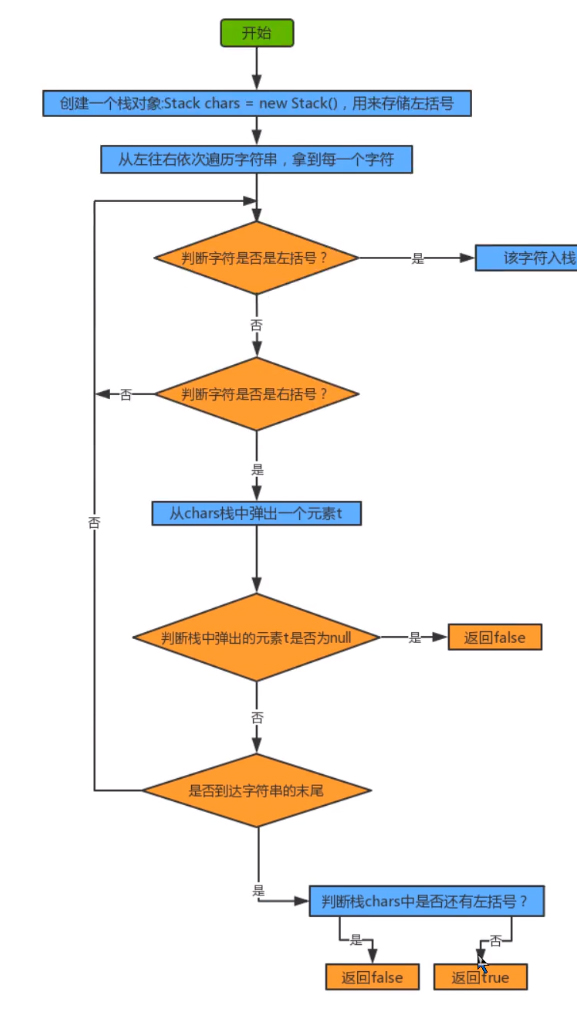
- code implementation
@Test
public void test1(){
String str = "(Shanghai)((Chang'an)";
boolean match = isMatch(str);
System.out.println(str + " Whether the brackets in match:" + match);
}
/**
* Use the stack to determine whether the left and right parentheses in str match
* @param str
* @return
*/
private boolean isMatch(String str){
// Create a stack to store the left parenthesis
Stack<String> stack = new Stack<>();
// Traverse the string from left to right and take out each character
String s;
for(int i=0;i<str.length();i++){
s = str.charAt(i)+"";
// Determine whether the character is an open parenthesis
if("(".equals(s)){
// If so, push into the stack
stack.push(s);
}else if(")".equals(s)){
// If it is a closing bracket, an element pops up from the stack
String t = stack.pop();
// If the pop-up element is null, there is no corresponding left parenthesis and false is returned
if(t==null){
return false;
}
// The pop-up element is not null, indicating that there is a corresponding left parenthesis. Continue the next cycle
}
// Not left and right parentheses, continue the next cycle
}
// After the loop ends, judge whether there are extra left parentheses in the stack. If so, it will not match and return false. Otherwise, it will return true
if(stack.isEmpty()){
return true;
}else{
return false;
}
}
(Shanghai)((Chang'an) Whether the brackets in match: false
2. Inverse Polish expression evaluation problem
The evaluation of inverse Polish expression is a kind of problem we often encounter in computers. To study and understand this problem, we must first understand what inverse Polish expression is? To understand inverse Polish expression, we must start with infix expression
- Infix expression
- Infix expressions are expressions used in our daily life, such as 1 + 3 * 2, 2 - (1 + 3), and so on
- Infix expressions are characterized by binary operators always placed between two operands
- Infix expression is people's favorite expression method, because it is simple and easy to understand. But it is not the case for computers, because the operation order of infix expression is not regular. Different operators have different priorities. If computers execute infix expression, they need to parse the expression semantics and do a lot of priority related operations
- Inverse Polish expression (suffix expression)
Inverse Polish expression is an expression representation first proposed by Polish logician J. lukasewicz in 1929. The characteristic of suffix expression is that the operator is always placed after its related operands
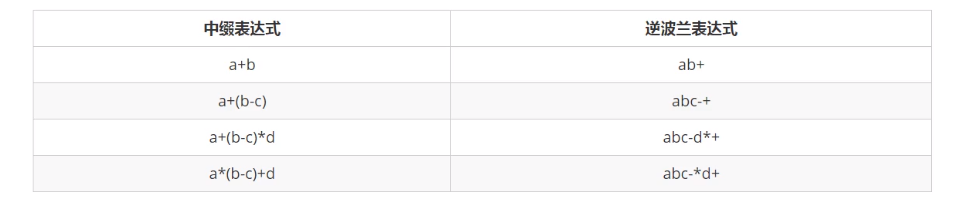
-
Requirements: given an array representation of an inverse Polish expression that contains only four operations of addition, subtraction, multiplication and division, find the result of the inverse Polish expression
-
analysis
-
Create a stack object oprands to store operands
-
Traverse the inverse Polish expression from left to right to get each string
-
Judge whether the string is an operator. If not, press the operand into the oprands stack
-
If it is an operator, two operands o1,o2 will pop up from the oprands stack
-
Use this operator to calculate o1 and o2 to get the result result
-
Push the result into the oprands stack
-
After traversal, take out the final result from the stack and return it
-
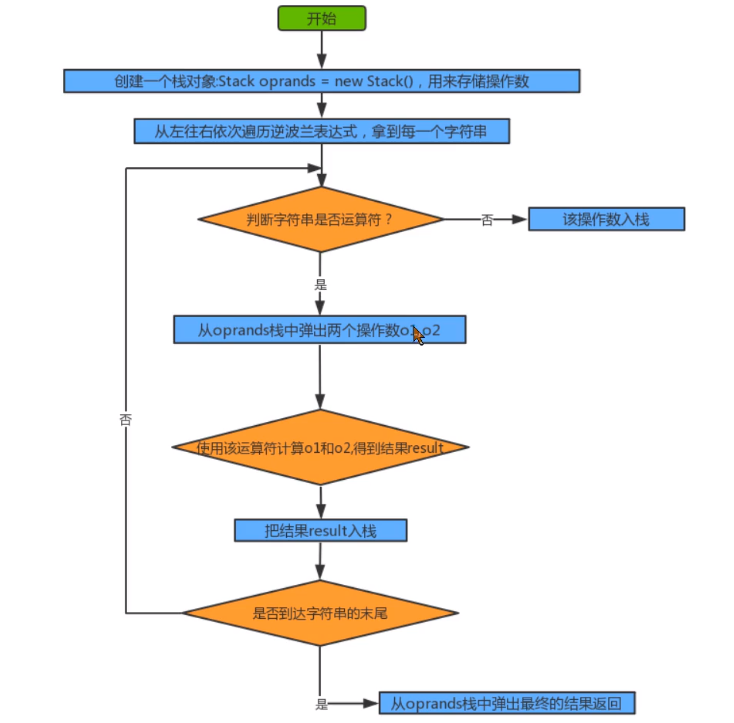
- code implementation
public class StackTest {
@Test
public void test2(){
// The inverse Polish expression of infix expression 3 * (17-15) + 18 / 6 is as follows: result 9
String[] notation = {"3", "17", "15", "-", "*", "18", "6", "/", "+"};
int result = caculate(notation);
System.out.println("The result of the inverse Polish expression is:" + result);
}
/**
* Calculate the result of the inverse Polish expression
* @param notation Array representation of inverse Polish expressions
* @return
*/
private int caculate(String[] notation){
// Create a stack object to store operands
Stack<Integer> oprands = new Stack<>();
// Traverse the inverse Polish expression from left to right to get each string
String curr;
Integer o1;
Integer o2;
for (int i = 0; i < notation.length; i++) {
curr = notation[i];
switch (curr){
case "+":
// If it is an operator, two operands o1,o2 will pop up from the oprands stack
o1 = oprands.pop();
o2 = oprands.pop();
// Use this operator to calculate o1 and o2, get the result, and push the result into the stack
oprands.push(o2 + o1);
break;
case "-":
// If it is an operator, two operands o1,o2 will pop up from the oprands stack
o1 = oprands.pop();
o2 = oprands.pop();
// Use this operator to calculate o1 and o2, get the result, and push the result into the stack
oprands.push(o2 - o1);
break;
case "*":
// If it is an operator, two operands o1,o2 will pop up from the oprands stack
o1 = oprands.pop();
o2 = oprands.pop();
// Use this operator to calculate o1 and o2, get the result, and push the result into the stack
oprands.push(o2 * o1);
break;
case "/":
// If it is an operator, two operands o1,o2 will pop up from the oprands stack
o1 = oprands.pop();
o2 = oprands.pop();
// Use this operator to calculate o1 and o2, get the result, and push the result into the stack
oprands.push(o2 / o1);
break;
default:
// Instead of an operator, push the operand into the oprands stack
oprands.push(Integer.parseInt(curr));
}
}
// After traversal, take out the final result from the stack and return it
return oprands.pop();
}
}
The result of the inverse Polish expression is: 9
5.4 queue
- Queue is a data structure based on first in first out (FIFO). It is a special linear table that can only be inserted at one end and deleted at the other end. It stores data according to the principle of first in first out. The data that enters first is read out first when reading data
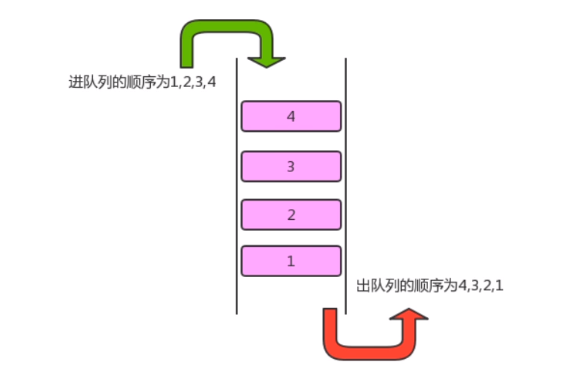
- API design
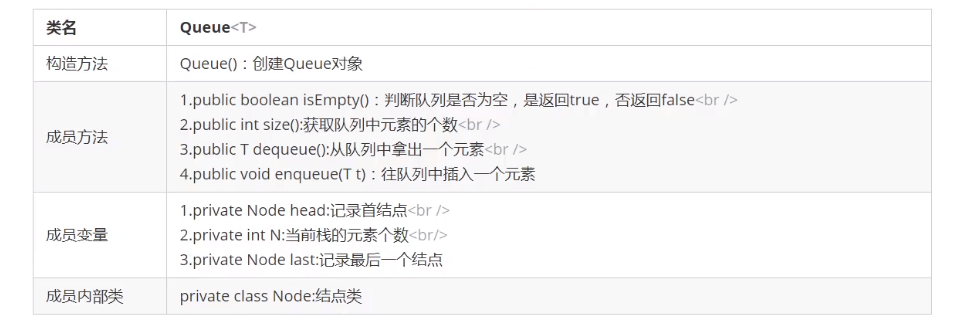
- code implementation
public class Queue<T> implements Iterable<T> {
/**
* First node
*/
private Node head;
/**
* Tail node
*/
private Node last;
/**
* Number of elements
*/
private int n;
/**
* constructor
*/
public Queue() {
this.head = new Node(null, null);
this.last = null;
this.n = 0;
}
/**
* Determine whether the queue is empty
*
* @return
*/
public boolean isEmpty() {
return n == 0;
}
/**
* Number of elements in the queue
*
* @return
*/
public int size() {
return n;
}
/**
* Save data to queue
*
* @param t
*/
public void enQueue(T t) {
if (isEmpty()) {
// Queue is empty
last = new Node(t, null);
head.next = last;
} else {
// Queue is not empty
Node oldLast = last;
last = new Node(t, null);
oldLast.next = last;
}
// Number of elements plus 1
n++;
}
/**
* Fetch data from queue
*
* @return
*/
public T deQueue() {
// When the queue is empty
if (isEmpty()) {
return null;
}
// If it is not empty, take the first node and point the first node to the second
Node oldFirst = head.next;
head.next = oldFirst.next;
// After fetching, judge whether the queue is empty
if (isEmpty()) {
last = null;
}
// Number of elements minus 1
n--;
return oldFirst.item;
}
/**
* iterator
*
* @return
*/
@Override
public Iterator<T> iterator() {
return new QIterator();
}
/**
* Iterator inner class
*/
private class QIterator implements Iterator<T> {
Node node;
public QIterator() {
this.node = head;
}
@Override
public boolean hasNext() {
return node.next != null;
}
@Override
public T next() {
node = node.next;
return node.item;
}
}
/**
* Node inner class
*/
private class Node {
T item;
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
public class QueueTest {
@Test
public void test() {
Queue<String> queue = new Queue<>();
queue.enQueue("a");
queue.enQueue("b");
queue.enQueue("c");
queue.enQueue("d");
for (Object q : queue) {
System.out.println(q);
}
System.out.println("------------");
String s = queue.deQueue();
System.out.println("The out of queue elements are:" + s);
System.out.println("Number of queues:" + queue.size());
}
}
a b c d ------------ The out of queue elements are: a Number of queues: 3
6. Symbol table
The main purpose of the symbol table is to associate a key with a value. The symbol table can store data elements as key value pair data composed of a key and a value. We can find the corresponding value according to the key
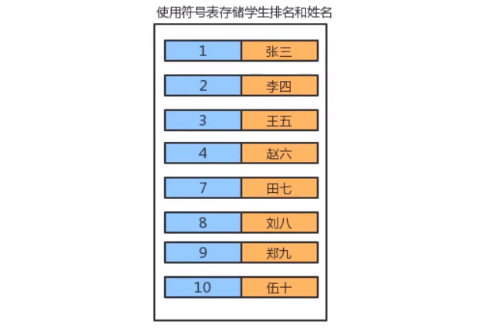
In the symbol table, the key is unique
Symbol tables are widely used in real life, as shown in the following table:

6.1 symbol table API design

6.2 implementation of symbol table
package chapter04;
/**
* @author Soil flavor
* Date 2021/9/6
* @version 1.0
* Symbol table
*/
public class SymbolTable<K, V> {
/**
* First node
*/
private Node head;
/**
* Number of elements
*/
private int n;
/**
* constructor
*/
public SymbolTable() {
this.head = new Node(null, null, null);
this.n = 0;
}
/**
* Get value corresponding to key
*
* @param key
* @return
*/
public V get(K key) {
Node node = head;
while (head.next != null) {
node = node.next;
if (node.key.equals(key)) {
return node.value;
}
}
return null;
}
/**
* Store chain value pairs into the symbol table
*
* @param key
* @param value
*/
public void put(K key, V value) {
// If there is a node with key in the table, replace the value with value
Node node = head;
while (node.next != null) {
// Move node pointer
node = node.next;
// judge
if (node.key.equals(key)) {
node.value = value;
return;
}
}
// If there is no node with key in the table, create a node and put it in front of the table (or at the end of the table, which is cumbersome to implement), and add 1 to the number of elements
Node oldFirst = head.next;
Node newNode = new Node(key, value, oldFirst);
head.next = newNode;
n++;
}
/**
* Delete key value pair of key
*
* @param key
*/
public void delete(K key) {
Node node = head;
while (node.next != null) {
// Judge whether the key of the next node of the node is equal to the key
if (node.next.key.equals(key)) {
// Equal; point the next node of the node to the next node
node.next = node.next.next;
// Number of elements minus 1
n--;
return;
}
// Move node batch needle
node = node.next;
}
}
/**
* Get the number of elements
*
* @return
*/
public int size() {
return n;
}
/**
* Internal node class
*/
private class Node {
private K key;
private V value;
private Node next;
public Node(K key, V value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
}
package chapter03;
import chapter04.SymbolTable;
import org.junit.Test;
/**
* @author Soil flavor
* Date 2021/9/6
* @version 1.0
* Test symbol table
*/
public class SymbolTableTest {
@Test
public void test(){
SymbolTable<Integer, String> st = new SymbolTable<>();
st.put(1, "a");
st.put(3, "b");
st.put(5, "c");
System.out.println(st.size());
st.put(1,"a1");
System.out.println(st.get(1));
System.out.println(st.size());
st.delete(1);
System.out.println(st.size());
}
}
3 a1 3 2
6.3 ordered symbol table
The previous symbol table is called unordered symbol table, because the order of key value pairs is not considered when inserting. In real life, it is sometimes necessary to sort according to the size of keys. The order should be considered when inserting data. Next, we will implement the ordered symbol table
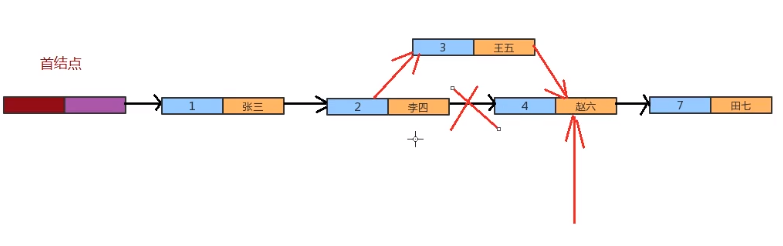
- code implementation
package chapter04;
/**
* @author Soil flavor
* Date 2021/9/6
* @version 1.0
* Ordered symbol table
* Sort by key when inserting
*/
public class OrderSymbolTable<K extends Comparable<K>, V> {
/**
* First node
*/
private Node head;
/**
* Number of elements
*/
private int n;
/**
* constructor
*/
public OrderSymbolTable() {
this.head = new Node(null, null, null);
this.n = 0;
}
/**
* Get value corresponding to key
*
* @param key
* @return
*/
public V get(K key) {
Node node = head;
while (head.next != null) {
node = node.next;
if (node.key.equals(key)) {
return node.value;
}
}
return null;
}
/**
* Store chain value pairs into the symbol table
*
* @param key
* @param value
*/
public void put(K key, V value) {
// Record current node
Node curr = head.next;
// Record previous node
Node pre = head;
// Traverse the symbol table and skip nodes smaller than key
while (curr != null && curr.key.compareTo(key) < 0) {
pre = curr;
curr = curr.next;
}
// After skipping nodes smaller than the key, the following are nodes equal to or greater than the key
// When it is equal to key, replace value and return
if (curr != null && curr.key.compareTo(key) == 0) {
curr.value = value;
return;
}
// When it is greater than key, a new node is created and inserted in front of the current node. The number of elements is increased by 1
Node newNode = new Node(key, value, curr);
pre.next = newNode;
n++;
}
/**
* Delete key value pair of key
*
* @param key
*/
public void delete(K key) {
Node node = head;
while (node.next != null) {
// Judge whether the key of the next node of the node is equal to the key
if (node.next.key.equals(key)) {
// equal; Point the next node to the next node
node.next = node.next.next;
// Number of elements minus 1
n--;
return;
}
// Move node batch needle
node = node.next;
}
}
/**
* Get the number of elements
*
* @return
*/
public int size() {
return n;
}
/**
* Internal node class
*/
private class Node {
private K key;
private V value;
private Node next;
public Node(K key, V value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
}
public class SymbolTableTest {
@Test
public void testOrderSymbolTable(){
OrderSymbolTable<Integer, String> st = new OrderSymbolTable<>();
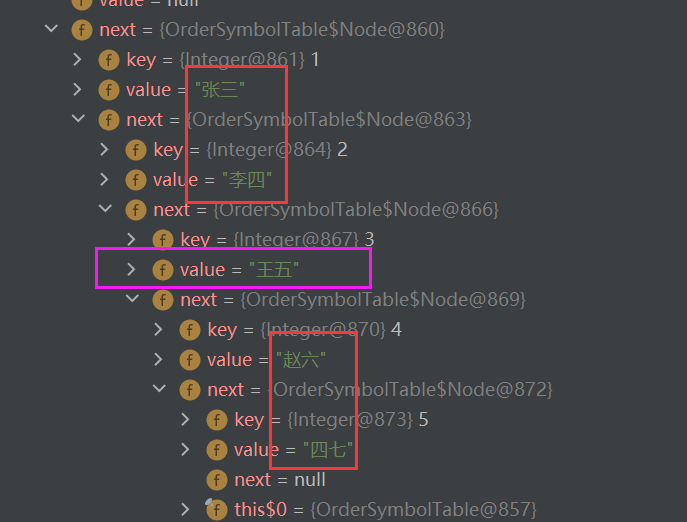
st.put(1,"Zhang San");
st.put(2,"Li Si");
st.put(4,"Zhao Liu");
st.put(5,"four seven");
st.put(3,"Wang Wu");
}
}