Least square (OLS) is a method to directly solve the parameters of linear regression equation with mathematical formula. Taking the simplest univariate linear regression as an example, formula 6-4 shows that a series of X values can calculate a series of predicted values y ', in order to minimize the error (Y- Y') between Y 'and y' of each pair of predictions. Since there are positive and negative errors, in order to avoid offsetting each other, we need to use the square of the error to measure. Although the absolute value can also avoid error cancellation, the algebraic computability of the absolute value is not as good as square, which is not convenient for differentiation. Double multiplication represents square, and the least square method represents the method of minimizing the sum of squares of errors.
Now let's use the code to manually implement a linear regression model and optimize the linear regression equation according to the least square method.

import pandas as pd

# Read abalone information
Abalone = pd.read_csv('AbaloneAgePrediction.txt',header=None)

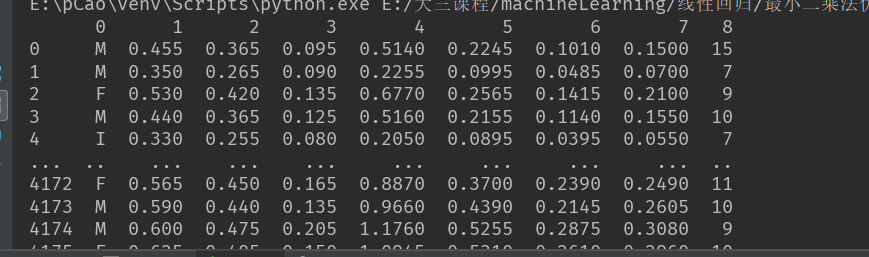
You can see that it is a DataFrame without column name. Modify its column name according to the information, and use the. corr() method to check its relevance.

Abalone.columns=['Sex', 'Length', 'Diameter', 'Height','Whole weight', 'Shucked weight',
                 'Viscera weight','Shell weight', 'Rings']  # Modify his column name based on the information

print(Abalone.corr())

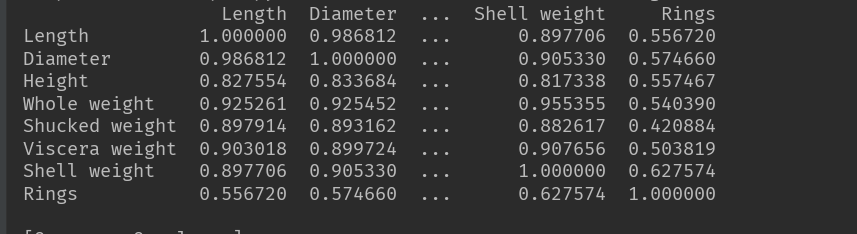
You can see that Rings and Shell weight have the highest correlation. So we only take these two columns (we just want to see the principle of the least squares method, so we only take two columns for verification)

AbaloneRing = Abalone[['Shell weight','Rings']]   # Take two columns according to the correlation

According to the publicity map above. We can know that what we want to calculate is:
c = (shell weight - average shell weight) * (abalone age - average abalone age) cumulative sum / (shell weight - average shell weight) cumulative sum of squares
b = average age of abalone - c * average shell weight
Let's write a function for this formula

def least_square_method(arg,arg2):
    c = ((arg-arg.mean())*(arg2-arg2.mean())).sum()/((arg-arg.mean())**2).sum()
    b = arg2.mean()-c*arg.mean()
    return c,b
    

use

c,b=least_square_method(AbaloneRing['Shell weight'],AbaloneRing['Rings'])

print(c,b)

output

Verification: we use LinearRegression in sklean to perform a fitting verification on the data

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(AbaloneRing[['Shell weight']],AbaloneRing['Rings'])  # Data requires data of a (- 1, 1) shape
print(model.coef_,model.intercept_)   # Output factor and intercept

The optimization function used in this LinearRegression is the least squares optimization

We can see the relationship between these data and the lines drawn by the least square formula in the form of drawing

import numpy as np
import matplotlib.pyplot as plt
x=np.arange(AbaloneRing['Shell weight'].min(),AbaloneRing['Shell weight'].max())
y=x*c+b
plt.scatter(AbaloneRing['Shell weight'],AbaloneRing['Rings'])
plt.plot(np.arange(AbaloneRing['Shell weight'].min(),AbaloneRing['Shell weight'].max()),y,color = 'red')
plt.ylabel('Rings')
plt.xlabel('shell weight')
plt.show()

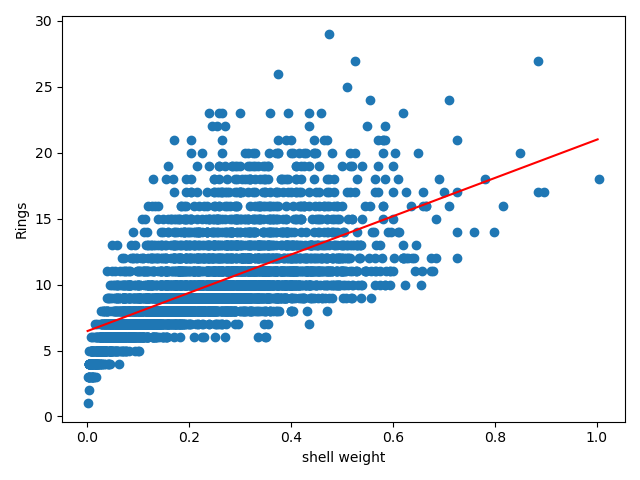
This is only a regression model with one parameter. If you want to build a linear regression model with multiple parameters. Then we have to deduce. In fact, I won't, but the good thing is that there is a direct formula

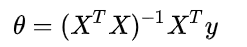
We just need to express this formula

def least_square_method(arg,arg2):
    X = np.hstack([np.ones((len(arg), 1)), arg])

    formula= np.linalg.inv(X.T.dot(X)).dot(X.T).dot(arg2)  # np.linalg.inv matrix inversion
    b = formula[0]     # intercept
    c = formula[1:]   # parameter

    return c,b

print(least_square_method(AbaloneRing[['Shell weight','Diameter']],AbaloneRing['Rings']))


from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(AbaloneRing[['Shell weight','Diameter']],AbaloneRing['Rings'])  # Data requires data of a (- 1, 1) shape
print(model.coef_,model.intercept_)   # Output factor and intercept

Contrast output

You can see that the output is the same as that in LinearRegression, so the formula is correct