Catalog
(1) definition
The line tree is a balanced binary search tree. What is balance? The absolute value of the height difference between the left and right subtrees of the line tree does not exceed 1. Each node of the line tree stores two parts:
- Interval or line segment: [left end of interval, right end of interval] (in the form of parameter or member attribute of node class)
- Storage elements of interval nodes: determined according to business requirements
Based on the characteristics of balanced binary tree (the absolute value of height difference between left and right subtrees is no more than 1), we can use NULL to complete the nonexistent interval, and finally complete it as a full binary tree. At this time, we can stack the interval nodes one by one in order (sequence output), so we can use array to represent a complete binary tree, Array needs a maximum of 4n storage space)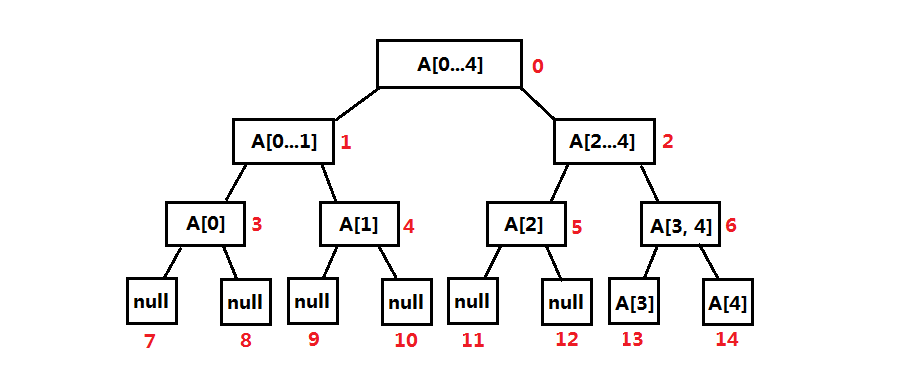
It can be seen from the above figure:
- The range of the left child interval of each node is [l, mid], and the right child is [mid+1, r]. Where l: left endpoint, r: right endpoint, mid = (L + r) / 2
- For node i, the left child node is 2*i + 1, and the right child node is 2*i + 2
(2) Custom line segment tree
1. Create line segment tree according to array
public class SegmentTree<E> { /** * Source data array */ private E[] data; /** * Represent the line tree as an array */ private E[] tree; /** * Fuser interface: the element stored in the interval node of the segment tree is determined by the merger() method of the fuser interface */ private Merger<E> merger; /** * Constructor: build the passed array into a line tree array * * @param arr */ @SuppressWarnings("unchecked") public SegmentTree(E[] arr, Merger<E> merger) { // Fuser interface initialization this.merger = merger; // Source data array initialization data = (E[]) new Object[arr.length]; for (int i = 0; i < arr.length; i++) { data[i] = arr[i]; } // The initialization size of the segment tree array is 4 times the array size tree = (E[]) new Object[4 * arr.length]; // Building line tree array buildSegmentTree(0, 0, arr.length - 1); } /** * Create a line segment tree representing the interval [l...r] at the treeIndex * * @param treeIndex Index of root node of segment tree * @param l Left end of interval * @param r Right endpoint of interval */ private void buildSegmentTree(int treeIndex, int l, int r) { // The termination condition of recursion: the left end of interval is equal to the right end of interval if (l == r) { tree[treeIndex] = data[l]; return; } // Left child node index of current node int leftTreeIndex = leftChild(treeIndex); // Right child node index of current node int rightTreeIndex = rightChild(treeIndex); // Intermediate value int mid = l + (r - l) / 2; // First, create a line segment tree with the interval [leftmost endpoint... Middle value] at the left child node index buildSegmentTree(leftTreeIndex, l, mid); // Then create a line segment tree with the interval [middle value + 1... Rightmost endpoint] at the right child node index buildSegmentTree(rightTreeIndex, mid + 1, r); // Finally, the data to be maintained in the interval is determined by the merge(e1, e2) method of the merge interface tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]); } /** * Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree * * @param index * @return */ private int leftChild(int index) { return index * 2 + 1; } /** * Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree * * @param index * @return */ private int rightChild(int index) { return index * 2 + 2; } @Override public String toString() { StringBuilder res = new StringBuilder(); res.append('['); for (int i = 0; i < tree.length; i++) { res.append(tree[i]); if (i != tree.length - 1) { res.append(", "); } } res.append("]"); return res.toString(); } }
test
public static void main(String[] args) { Integer[] nums = {1, 2, 3, 4, 5, 6}; // lambda expression (a, b) - > A + B represents the merge(a, b) of the merge interface, and the sum of the two numbers is obtained SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, (a, b) -> a + b); System.out.println(segmentTree); }

2. interval query operation of line segment tree
There are three situations:
- The left child interval of the line tree contains the search interval (mid > = right endpoint of the query interval), recursively entering the left child interval
- The right child interval of the line tree contains the search interval (mid < = left end of the query interval), recursively entering the right child interval
- The search interval has left and right child intervals of the line tree at the same time. Obtain the values of [left endpoint of the query interval, mid] and [mid, right endpoint of the query interval] for operation
/** * Return the value of interval [queryl, queryre] * * @param queryL * @param queryR * @return */ public E query(int queryL, int queryR) { if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryR < queryL) { throw new IllegalArgumentException("Index is illegel."); } return query(0, 0, data.length - 1, queryL, queryR); } /** * In the range of [r...l] in the segment tree whose root is treeIndex, search the value of the interval [queryll... Queryre] * * @param treeIndex * @param l * @param r * @param queryL * @param queryR * @return */ private E query(int treeIndex, int l, int r, int queryL, int queryR) { // Recursive termination condition: the left end of the search interval is equal to the left end of the line tree whose root is treeIndex, and the right end of the search interval is equal to the right end of the line tree whose root is treeIndex if (l == queryL && r == queryR) { return tree[treeIndex]; } int leftTreeIndex = leftChild(treeIndex); int rightTreeIndex = rightChild(treeIndex); int mid = l + (r - l) / 2; // 3 if (queryR <= mid) { // The first case: the left subtree interval of the line segment tree with treeIndex as the root contains the search interval return query(leftTreeIndex, l, mid, queryL, queryR); } else if (queryL >= mid + 1) { // The second case: the right subtree interval of the line segment tree with treeIndex as the root contains the search interval return query(rightTreeIndex, mid + 1, r, queryL, queryR); } else { // The third case: the search interval is contained in the left and right subtree intervals of the line segment tree with treeIndex as the root E leftResult = query(leftTreeIndex, l, mid, queryL, mid); E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR); return this.merger.merge(leftResult, rightResult); } }
3. Single update operation of line tree
Update the values of index index index in the segment tree, and maintain the values of all its parent nodes
/** * Update the value of index position to e * * @param index * @param e */ public void set(int index, E e) { if (index < 0 || index >= data.length) { throw new IllegalArgumentException("Index is Illegal."); } data[index] = e; set(0, 0, data.length - 1, index, e); } /** * Update the value of index to e in the segment tree with treeIndex as root * * @param treeIndex * @param l * @param r * @param index * @param e */ private void set(int treeIndex, int l, int r, int index, E e) { // Conditions for recursive termination: the left end of the search interval is equal to the right end of the search interval. Find the position of the index index in the segment tree if (l == r) { tree[treeIndex] = e; return; } int leftTreeIndex = leftChild(treeIndex); int rightTreeIndex = rightChild(treeIndex); int mid = l + (r - l) / 2; if (index <= mid) { // The left subtree interval of a line segment tree with treeIndex as its root contains index set(leftTreeIndex, l, mid, index, e); } else { // index >= mid + 1 // The right subtree interval of a line segment tree with treeIndex as its root contains index set(rightTreeIndex, mid + 1, r, index, e); } // Reassign merge to the parent node of the modified element node tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]); }
(3) Time complexity analysis
| function | Time complexity | Analysis |
|---|---|---|
| query(l, r) | O(h) => O(logn) | The user-defined line tree is a full binary tree, and the query operation only needs recursion at the height of the tree |
| set(index, e) | O(h) => O(logn) | The custom line tree is a full binary tree, and the update operation only needs to recurse at the height of the tree |

