Preface:
Originally decided to learn data structure to learn things, the result has been Gu until now..
Line tree is a kind of advanced data structure.
It is a kind of binary tree, that is to say, for a line segment, we will use a binary tree to represent it.
Text:
Line tree can do single point query, single point modification, interval query, interval modification
Generally, line trees are
Let's give you an example
Now I have a string of numbers:

Put him in a line segment tree, and it will be like this: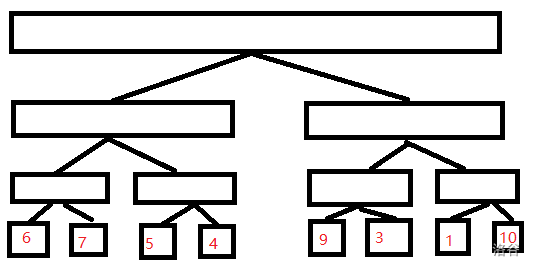
Then the father of each leaf node is the sum of his son's values, which is a common line tree: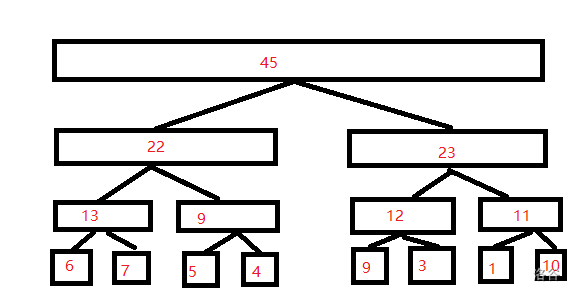
We mark each node with serial number in order: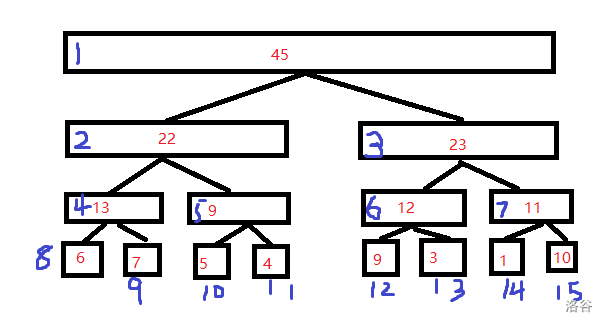
We find that the serial number of each node's son is related to its own serial number - its own serial number is a, the left son's serial number 2a, and the right son's serial number 2a+1.
So, we can recursively build a line segment tree from the bottom up.
Definition
int input[500005];//An array used to hold input.
struct node{
int l,r,sum;//l and r represent the range represented by the current node, and sum is the value of this node.
}tree[4*500005];//The space of the line tree should be opened to 4 times of the original array, otherwise it will die miserably.Build up trees
void build(int i,int l,int r){//Recursive tree building, generally speaking, when calling, i's position is filled with 1, l and r are filled with the first sequence number and the last sequence number of the input array respectively.
tree[i].l=l;tree[i].r=r;
if(l==r){//If this node is a leaf node
tree[i].sum=input[l];
return ;
}
int mid=(l+r)>>1;
build(i*2,l,mid);
build(i*2+1,mid+1,r);//Construct left subtree and right subtree respectively
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//Then the son pushes it to the father.
return ;
}Next let's learn some basic operations
Interval modification
If this interval is completely included in the target interval, let's say that this interval marks k
Code
inline void add(int i,int l,int r,int k){
if(tree[i].l>=l && tree[i].r<=r){//If this interval is completely included in the target interval, let's say that this interval marks k
tree[i].sum+=k;
return ;
}
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
}Single point query
The so-called single point query is to ask you what the current value of the * th number is after a meal of addition and subtraction.
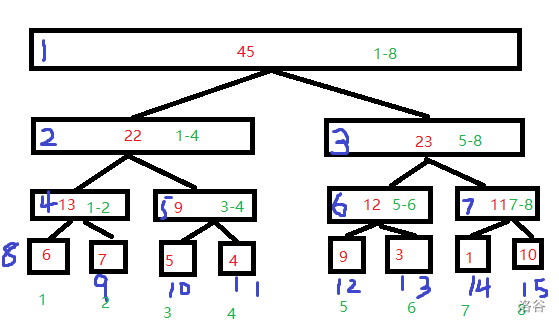
Here's an example: I want to know the value of the fifth number now.
The following search is generated
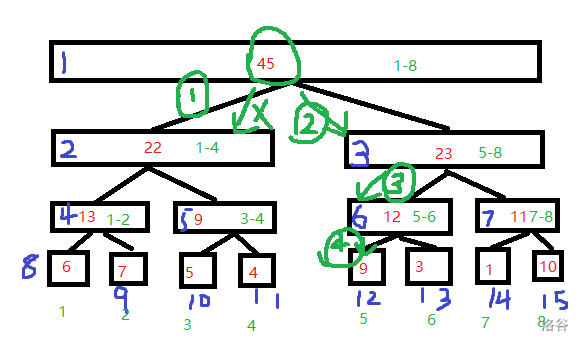
The search is based on the scope of the node. If it happens to be this node, it will be output directly. If it is included in this node, continue refining.
Code
void search(int i,int dis){
if(tree[i].l==tree[i].r) {
return tree[i].sum;
}
int mid=(tree[i].l+tree[i].r)/2;
if(dis<=mid) return search(i*2,dis);
else return search(i*2+1,dis);
}---------------------------------------------------Dividing line------------------------------------------------------------------------------
Interval query
Similar to a single point query, it can be understood as a single point query. Some nodes just contain this interval, which can be added directly.
Code
int search(int i,int l,int r){
if(tree[i].l>=l&&tree[i].r<=r)
return tree[i].sum;
if(tree[i].r<l||tree[i].l>r) return 0;
int s=0;
if(tree[i*2].r>=1) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}Single point modification
We build the tree from the bottom to the top, and modify it from the top to the bottom when a single point is modified. As long as the nodes containing the target point are added with the same number, it is OK.
Code
inline void add(int i,int dis,int k){
if(tree[i].l==tree[i].r){
tree[i].sum+=k;
return;
}
if(dis<=tree[i*2].r&&dis>=tree[i*2].l) tree[i].sum+=k,add(i*2,dis,k);
else if(dis<=tree[i*2+1].r&&dis>=tree[i*2+1].l) tree[i].sum+=k,add(i*2+1,dis,k);
}Note: the above interval modification and interval query cannot be shared. You will know why
Now we need to implement inter modification and interval query. If we put the above two together, there will be a problem. When the interval to be queried is not completely included in the modified interval, there will be a problem, so we need to use the lazy flag.
Principle: when the above situation occurs, first pass the lazy mark, and then judge.
Code (i.e. code of line tree template question 1)
void pushdown(ll i){
if(tree[i].lazy!=0){
tree[i*2].lazy+=tree[i].lazy;
tree[i*2+1].lazy+=tree[i].lazy;
ll mid=(tree[i].l+tree[i].r)/2;
tree[i*2].num+=tree[i].lazy*(mid-tree[i*2].l+1);
tree[i*2+1].num+=tree[i].lazy*(tree[i*2+1].r-mid);
tree[i].lazy=0;
}
return ;
}
void add(ll i,ll l,ll r,ll k){
if(tree[i].r<=r&&tree[i].l>=l) {
tree[i].num+=k*(tree[i].r-tree[i].l+1);
tree[i].lazy+=k;
return;
}
pushdown(i);
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].num=tree[i*2].num+tree[i*2+1].num;
return;
}
ll search(ll i,ll l,ll r)
{
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].num;
if(tree[i].r<l||tree[i].l>r) return 0;
pushdown(i);
ll s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}Multiplication in line tree template 2
At this time, it can't be done like addition, because the order of operations is different with different operators.
This requires us to consider whether to add and multiply first or to multiply and add first when the lazy mark subscript is passed. We just need to do this for lazy tags.
There are two kinds of lazy markers, plz of addition and mlz of multiplication.
The code is similar to the above, with one more function
(line tree template question 2) code
void pushdown(ll i){
ll k1=tree[i].mlz,k2=tree[i].plz;
tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;
tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
tree[i].plz=0;
tree[i].mlz=1;
return ;
}
inline void mul(ll i,ll l,ll r,ll k){
if(tree[i].r<l || tree[i].l>r) return ;
if(tree[i].l>=l && tree[i].r<=r){
tree[i].sum=(tree[i].sum*k)%p;
tree[i].mlz=(tree[i].mlz*k)%p;
tree[i].plz=(tree[i].plz*k)%p;
return ;
}
pushdown(i);
if(tree[i<<1].r>=l) mul(i<<1,l,r,k);
if(tree[i<<1|1].l<=r) mul(i<<1|1,l,r,k);
tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
return ;
}
void add(ll i,ll l,ll r,ll k){
if(tree[i].r<l || tree[i].l>r) return ;
if(tree[i].l>=l && tree[i].r<=r){
tree[i].sum+=((tree[i].r-tree[i].l+1)*k)%p;
tree[i].plz=(tree[i].plz+k)%p;
return ;
}
pushdown(i);
if(tree[i<<1].r>=l) add(i<<1,l,r,k);
if(tree[i<<1|1].l<=r) add(i<<1|1,l,r,k);
tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
return ;
}
ll search(ll i,ll l,ll r){
if(tree[i].r<l || tree[i].l>r) return 0;
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].sum;
pushdown(i);
ll sum=0;
if(tree[i<<1].r>=l) sum+=search(i<<1,l,r)%p;
if(tree[i<<1|1].l<=r) sum+=search(i<<1|1,l,r)%p;
return sum%p;
}Finally, put the codes of the four template questions in place
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if(x < 0) {
putchar('-');
x = -x;
}
if(x > 9)
write(x/10);
putchar(x % 10 + '0');
return;
}
int n,m,p;
int input[500005];
struct node{
int l,r,sum;
}tree[4*500005];
inline void build(int i,int l,int r){
tree[i].l=l,tree[i].r=r;
if(l==r){
tree[i].sum=input[l];
return;
}
int mid=(l+r)>>1;
build(i*2,l,mid);build(i*2+1,mid+1,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
return;
}
inline int search(int i,int l,int r){
if(tree[i].l>=l&&tree[i].r<=r)
return tree[i].sum;
if(tree[i].r<l||tree[i].l>r) return 0;
int s=0;
if(tree[i*2].r>=1) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}
inline void add(int i,int dis,int k){
if(tree[i].l==tree[i].r){
tree[i].sum+=k;
return;
}
if(dis<=tree[i*2].r) add(i*2,dis,k);
else add(i*2+1,dis,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
}
int main(){
int a,b,c,d;
read(n),read(m);
for(int i=1;i<=n;i++)
read(input[i]);
build(1,1,n);
for(int i=1;i<=m;i++){
read(a),read(b),read(c);
if(a==1){
add(1,b,c);
}
else{
write(search(1,b,c)),cout<<endl;
}
}
}#include<bits/stdc++.h>
using namespace std;
template <typename T>
void read(T &x) {
x = 0;
int f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;
}
template <typename T>
void write(T x)
{
if(x < 0) {
putchar('-');
x = -x;
}
if(x > 9)
write(x/10);
putchar(x % 10 + '0');
return;
}
int n,m,a,b,c,ans,f;
struct Tree{
int l,r,num;
}tree[500005*4];
int input[500005];
inline void build(int i,int l,int r){
tree[i].l=l,tree[i].r=r;
if(l==r){
tree[i].num=input[l];
return;
}
int mid=(l+r)/2;
build(i*2,l,mid);build(i*2+1,mid+1,r);
tree[i].num=tree[i*2].num+tree[i*2+1].num;
}
inline void add(int i,int l,int r,int k)
{
if(tree[i].l>=l&&tree[i].r<=r){
tree[i].num+=k;
return;
}
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
}
inline void search(int i,int dis){//The code here is different from the one mentioned above, all of which are OK.
ans+=tree[i].num;
if(tree[i].l==tree[i].r) {
return ;
}
int mid=(tree[i].l+tree[i].r)/2;
if(dis<=mid) search(i*2,dis);
if(dis>mid) search(i*2+1,dis);
}
int main(){
read(n),read(m);
build(1,1,n);
for(int i=1;i<=n;i++)
read(input[i]);
for(int i=1;i<=m;i++)
{
read(f);
if(f==1){
read(a),read(b),read(c);
add(1,a,b,c);
}
else{
ans=0;
read(a);
search(1,a);
cout<<ans+input[a]<<endl;
}
}
}
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template <typename T>
inline void read(T &x) {
x = 0;
ll f = 1;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1;
ch = getchar();
}
while (isdigit(ch)) {
x = x * 10 + (ch ^ 48);
ch = getchar();
}
x *= f;
return;}
template <typename T>
inline void write(T x){
if(x < 0) {
putchar('-');
x = -x;
}
if(x > 9)
write(x/10);
putchar(x % 10 + '0');
return;
}
ll n,m,input[500005],a,b,c,d;
struct Tree{
ll l,r,num,lazy;
}tree[500005*4];
inline void build(ll i,ll l,ll r){
tree[i].l=l,tree[i].r=r;
if(l==r){
tree[i].num=input[l];
return;
}
ll mid=(l+r)/2;
build(i*2,l,mid);
build(i*2+1,mid+1,r);
tree[i].num=tree[i*2].num+tree[i*2+1].num;
}
inline void pushdown(ll i){
if(tree[i].lazy!=0){
tree[i*2].lazy+=tree[i].lazy;
tree[i*2+1].lazy+=tree[i].lazy;
ll mid=(tree[i].l+tree[i].r)/2;
tree[i*2].num+=tree[i].lazy*(mid-tree[i*2].l+1);
tree[i*2+1].num+=tree[i].lazy*(tree[i*2+1].r-mid);
tree[i].lazy=0;
}
return ;
}
inline void add(ll i,ll l,ll r,ll k){
if(tree[i].r<=r&&tree[i].l>=l) {
tree[i].num+=k*(tree[i].r-tree[i].l+1);
tree[i].lazy+=k;
return;
}
pushdown(i);
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].num=tree[i*2].num+tree[i*2+1].num;
return;
}
inline ll search(ll i,ll l,ll r)
{
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].num;
if(tree[i].r<l||tree[i].l>r) return 0;
pushdown(i);
ll s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);
return s;
}
int main(){
read(n),read(m);
for(register ll i=1;i<=n;i++)
read(input[i]);
build(1,1,n);
for(register ll i=1;i<=m;i++){
read(d);
if(d==1) read(a),read(b),read(c),add(1,a,b,c);
else read(a),read(b),write(search(1,a,b)),cout<<'\n';
}
} #include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,p;
ll input[100010];
struct node{
ll l,r;
ll sum,mlz,plz;
}tree[4*100010];
inline void build(ll i,ll l,ll r){
tree[i].l=l;
tree[i].r=r;
tree[i].mlz=1;
if(l==r){
tree[i].sum=input[l]%p;
return ;
}
ll mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
return ;
}
inline void pushdown(ll i){
ll k1=tree[i].mlz,k2=tree[i].plz;
tree[i<<1].sum=(tree[i<<1].sum*k1+k2*(tree[i<<1].r-tree[i<<1].l+1))%p;
tree[i<<1|1].sum=(tree[i<<1|1].sum*k1+k2*(tree[i<<1|1].r-tree[i<<1|1].l+1))%p;
tree[i<<1].mlz=(tree[i<<1].mlz*k1)%p;
tree[i<<1|1].mlz=(tree[i<<1|1].mlz*k1)%p;
tree[i<<1].plz=(tree[i<<1].plz*k1+k2)%p;
tree[i<<1|1].plz=(tree[i<<1|1].plz*k1+k2)%p;
tree[i].plz=0;
tree[i].mlz=1;
return ;
}
inline void mul(ll i,ll l,ll r,ll k){
if(tree[i].r<l || tree[i].l>r) return ;
if(tree[i].l>=l && tree[i].r<=r){
tree[i].sum=(tree[i].sum*k)%p;
tree[i].mlz=(tree[i].mlz*k)%p;
tree[i].plz=(tree[i].plz*k)%p;
return ;
}
pushdown(i);
if(tree[i<<1].r>=l) mul(i<<1,l,r,k);
if(tree[i<<1|1].l<=r) mul(i<<1|1,l,r,k);
tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
return ;
}
inline void add(ll i,ll l,ll r,ll k){
if(tree[i].r<l || tree[i].l>r) return ;
if(tree[i].l>=l && tree[i].r<=r){
tree[i].sum+=((tree[i].r-tree[i].l+1)*k)%p;
tree[i].plz=(tree[i].plz+k)%p;
return ;
}
pushdown(i);
if(tree[i<<1].r>=l) add(i<<1,l,r,k);
if(tree[i<<1|1].l<=r) add(i<<1|1,l,r,k);
tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%p;
return ;
}
inline ll search(ll i,ll l,ll r){
if(tree[i].r<l || tree[i].l>r) return 0;
if(tree[i].l>=l && tree[i].r<=r)
return tree[i].sum;
pushdown(i);
ll sum=0;
if(tree[i<<1].r>=l) sum+=search(i<<1,l,r)%p;
if(tree[i<<1|1].l<=r) sum+=search(i<<1|1,l,r)%p;
return sum%p;
}
int main(){
scanf("%lld%lld%lld",&n,&m,&p);
for(int i=1;i<=n;i++) scanf("%lld",&input[i]);
build(1,1,n);
for(int i=1;i<=m;i++){
ll f1,a,b,c;
scanf("%lld",&f1);
if(f1==1)
scanf("%lld%lld%lld",&a,&b,&c),mul(1,a,b,c);
if(f1==2)
scanf("%lld%lld%lld",&a,&b,&c),add(1,a,b,c);
if(f1==3)
scanf("%lld%lld",&a,&b),printf("%lld\n",search(1,a,b));
}
return 0;
}