Title Link: Where to Run? - LightOJ 1287 - Virtual Judge (ppsucxtt.cn)

Topic meaning: there are n cities, numbered 0~n-1, and there are m right undirected edges. The edge right represents the time it takes to pass through this edge. A thief starts from the city numbered 0, and he will not go to the city he has passed. Every time he arrives at a city, he will make a choice, either stay in the city for 5 minutes or go to the next city, The next city he went to was of the following nature:

(1) In this city, you can traverse all the remaining cities without passing through the already passed cities

(2) The probability of choosing any city satisfying the nature is the same, and the probability of thieves staying in the original city is the same

Analysis: this problem is obviously a probability dp. Since we have to traverse all cities, we must record the set of cities that have been traversed and know the current city, so we can think of using shape pressure dp to solve it.

dp[i][j] indicates the time expectation for the thief to traverse all cities when the current city I and the traversed city state is J. we can preprocess the number of cities cnt[i][j] that the thief can go to when the city I and the traversed city state is j, then the probability that the thief may go to each city in the next step is 1 / (1+cnt[i][j]), The probability of the thief staying in the current city is also 1 / (1+cnt[i][j]), so there is the following probability dp analysis:

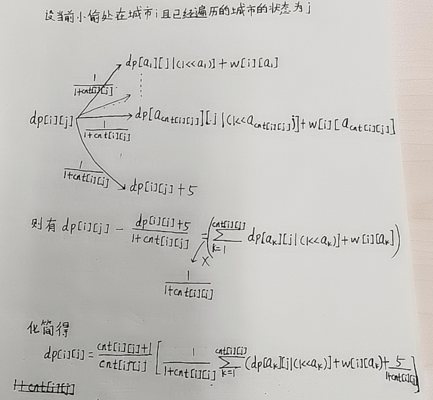
  The probability dp transfer equation has been solved, and now the difference is solved in cnt[i][j]. This is preprocessed by memory search. There are detailed comments in the code, so I won't repeat it. You can refer to the following code:

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int N=16;
int h[N],ne[1<<N],e[1<<N],w[1<<N],idx;
int cnt[N][1<<N];//cnt[i][j] indicates the number of optional roads when the current position is I and the status is j 
int f[N][1<<N];//Memory array for cnt array settings
double dp[N][1<<N];//dp[i][j] indicates the expected time required to traverse the city when the current position is I and the status is j 
int n,m,x,y,z,End;
void add(int x,int y,int z)
{
	e[idx]=y;
	w[idx]=z;
	ne[idx]=h[x];
	h[x]=idx++;
}
int dfs(int x,int State)
{
	if(State==End) return f[x][State]=1;//1 cannot be returned directly. To update the value in termination status, it will be used in DP 
	if(f[x][State]) return f[x][State];
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		//If you go to the city you have already passed, or if you go to the j-th City, you can't go all over. All cities will be skipped 
		if((State>>j&1)||!dfs(j,State|(1<<j))) continue;
		f[x][State]=1;//The next step is to go to the j City, which can achieve the purpose of visiting all cities 
		cnt[x][State]++;//The number of cities you can go next + 1 when you are currently in the x city and the status is j 
	}
	return f[x][State];
}
double DP(int x,int State)
{
	if(State==End||cnt[x][State]==0) return 0;//0 should be returned when reaching the termination state or the state that does not meet the meaning of the question 
	if(dp[x][State]) return dp[x][State];
	double p=1.0/(cnt[x][State]+1);
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if((State>>j&1)||!f[j][State|(1<<j)]) continue;
		dp[x][State]+=(DP(j,State|(1<<j))+w[i])*p;
	}
	dp[x][State]+=5*p;
	dp[x][State]/=(1-p);
	return dp[x][State];
}
int main()
{
	int T;
	cin>>T;
	for(int o=1;o<=T;o++)
	{
		memset(h,-1,sizeof h);
		memset(f,0,sizeof f);
		memset(cnt,0,sizeof cnt);
		memset(dp,0,sizeof dp); 
		scanf("%d%d",&n,&m);
		idx=0;End=(1<<n)-1;
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d%d",&x,&y,&z);
			add(x,y,z);add(y,x,z);
		}
		dfs(0,1);
		printf("Case %d: %.10lf\n",o,DP(0,1));
	}
	return 0;
}