Topic 1
thinking
Interval DP
To play DP, first determine why it is DP, then the old four. First find several States, assign initial values, find transfers, and finally find the answer.
Determination algorithm
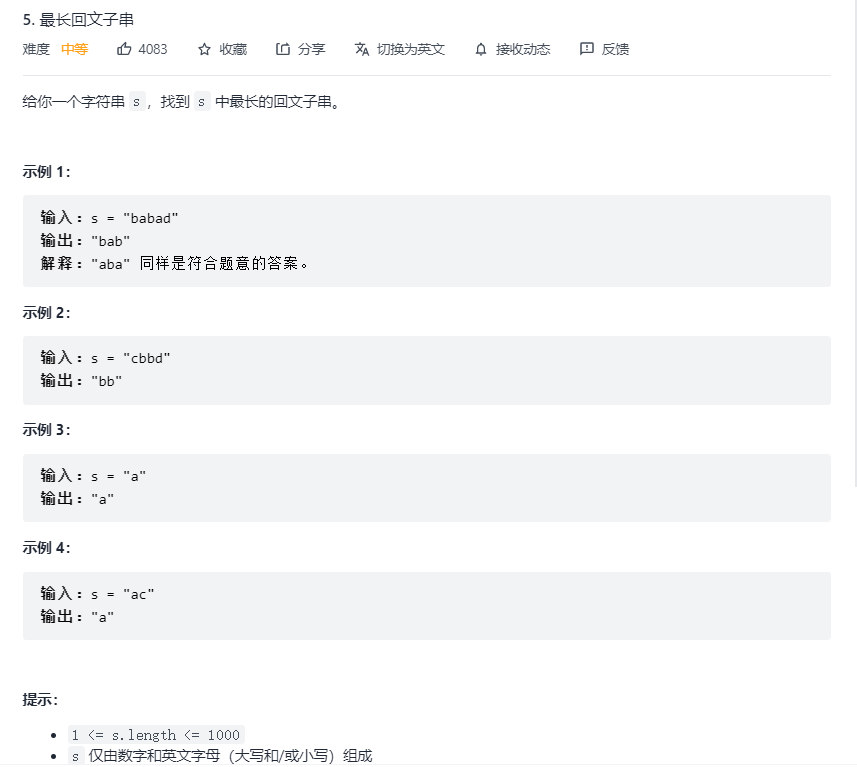
If abba is a palindrome string, bb must be a palindrome string. Therefore, abstract whether abba is a palindrome string and whether bb is a palindrome string. When bb is a palindrome string, that is, the small problem is established, and the left and right endpoints are consistent, it is deduced that the large problem is established, so you can try DP algorithm
Steady state
Because it is a substring, it is a continuous subsequence, so you only need to represent the interval of the subsequence, so you can use I and j to represent the interval.
Find the initial value (empty string or left and right characters)
The palindrome string must be judged by the left and right nodes together, so the initial value is a single one character case and two characters case.
Find transfer
As shown in the above analysis (how can a small problem lead to a big problem), when the two ends are the same, the results of a large interval depend on the results between cells, so
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1];
}
Find the answer
1. In fact, the key to this question is to find the answer. The longest substring he wants. If the question is only to find the length of the longest substring, use dp [] []. Either the palindrome substring is 0, or the storage length is 0.
2. But this problem needs to find out the substring, so using substr method, you need to know the starting point + length, so the two information cannot be saved. Then dp [] [] normally stores the bool value, and the starting point + length is calculated separately. Because our search order is from small to large, and the weight requirement only requires the maximum length, which is allowed for different strings with the same length, as long as we find a palindrome substring, we will record the starting point + length, because we search from small to large. After the last update, it must be the largest, that is, the answer.
code
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
int begin = 0, max_length = 0;
bool dp[1050][1050] = { false };//initialization
for (int i = 0; i < n; i++) {//initialization
dp[i][i] = true;
begin = i;//If it is a palindrome substring, the starting point and length will be updated
max_length = 1;
}
for (int i = 0; i < n - 1; i++) {//initialization
if (s[i] == s[i + 1]) {
dp[i][i + 1] = true;
begin = i;//If it is a palindrome substring, the starting point and length will be updated
max_length = 2;
}
}
for (int l = 2; l < n; l++) {
for (int i = 0, j; i + l < n; i++) {
j = i + l;
if (s[i] == s[j]) {//When both ends are the same, the result of a large interval depends on the difference between cells
if (dp[i + 1][j - 1]) {//If it is a palindrome substring, the starting point and length will be updated
begin = i;
max_length = l + 1;
}
dp[i][j] = dp[i + 1][j - 1];
}
}
}
return s.substr(begin, max_length);
}
};
(all codes have been run correctly on the force buckle)
After testing, the running condition of the code is (the shortest time obtained after multiple tests):

Time complexity: O(N^2)
Space complexity: O(N^2)
Topic 2:

thinking
For the requirements of direct simulation, pay attention to rewriting the internal operator < of the structure before sorting with STL
code
//202009-1 Scale checkpoint query
#include <iostream>
#include <algorithm>
#include <unordered_set>
using namespace std;
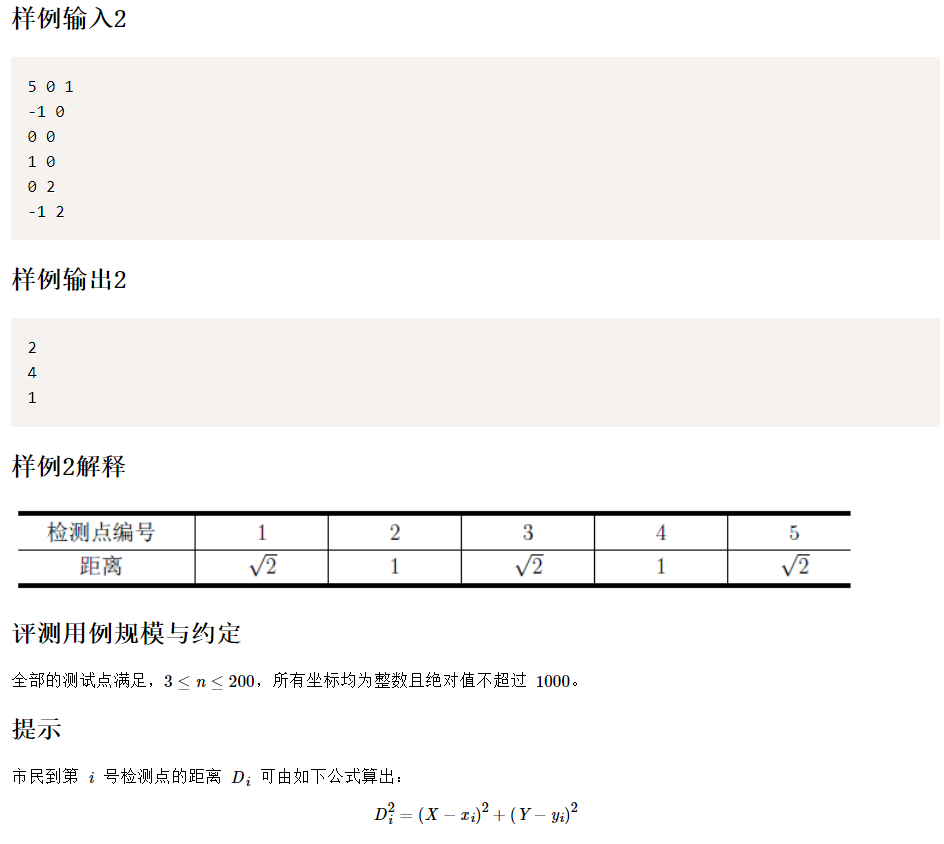
int n, x, y;//Total points, target person coordinates
struct position {
int x;
int y;
int id;//Monitoring point serial number
long long distance;//Distance. In order to prevent overflow, open long long
bool operator < (const position& p)const {//Override the operator < method in order to use the sort function
if (distance == p.distance) {//Those with equal distances should be numbered smaller
return id < p.id;
}
return distance < p.distance;//First, it's smaller than the distance
}
};
position p[201];
int main()
{
cin >> n >> x >> y;
for (int i = 0; i < n; i++) {
scanf("%d %d", &p[i].x, &p[i].y);
p[i].id = i + 1;
p[i].distance = (p[i].x - x)*(p[i].x - x) + (p[i].y - y)*(p[i].y - y);
}
sort(p, p + n);//Sort from small to large
for (int i = 0; i < 3; i++) {
printf("%d\n", p[i].id);
}
return 0;
}
(all codes have been run correctly on the force buckle)
After testing, the running condition of the code is (the shortest time obtained after multiple tests):

Time complexity: O(N)
Topic 3

Idea:
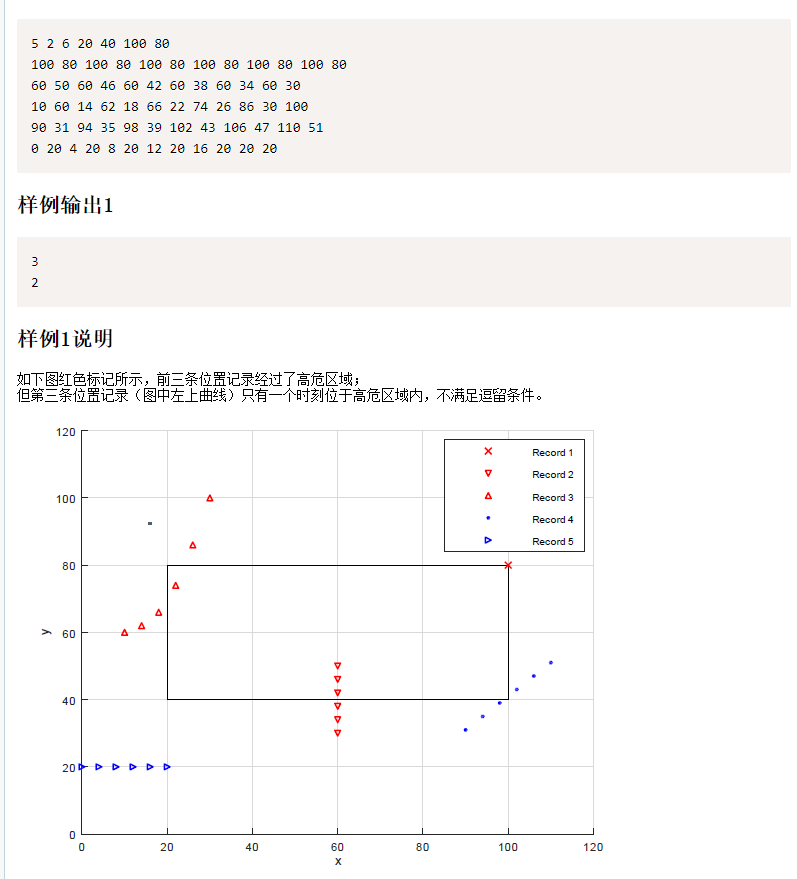
Direct simulation is OK, but note that the number of people passing through high-risk areas here refers to passing by, while staying refers to k consecutive points in high-risk areas, and the two are counted separately
code:
//202009-2 Screening of risk population
#include <iostream>
#include <algorithm>
#include <unordered_set>
using namespace std;
int n, k, t, xl, yd, xr, yu;//See the title for the meaning
int main()
{
int ans_linger = 0;//Number of stay - as long as passing through high-risk areas
int ans_pass = 0;//Number of channels
cin >> n >> k >> t >> xl >> yd >> xr >> yu;
for (int i = 0; i < n; i++) {//Control the i-th person
int tmp_x, tmp_y, cnt = 0;
bool is_visited = false;//See if there is a high risk
bool is_judged = false;//Are k consecutive points at high risk
for (int j = 0; j < t; j++) {//The j-th point of the i-th person (xj,yj)
scanf("%d %d", &tmp_x, &tmp_y);
if (tmp_x >= xl && tmp_x <= xr && tmp_y >= yd && tmp_y <= yu) {
cnt++;
is_visited = true;//true when passing by
if (cnt >= k && !is_judged) {//Once k points in a row
ans_linger++;
is_judged = true;//Continuous k points can be judged as staying once, and then not in judgment
}
}
else {
if (cnt) {//This is because there are not k consecutive points and it does not count as staying, so it should be cleared
cnt = 0;
}
}
}
if (is_visited) {
ans_pass++;
}
}
printf("%d\n", ans_pass);
printf("%d", ans_linger);
}
(all codes have been run correctly on the force buckle)
After testing, the running condition of the code is (the shortest time obtained after multiple tests):
Time complexity: O(N^2)