A topic meaning

Given n n n n n n n n, m and k, find out how many pairs (i,j) make (C_i^j ) multiply K for all I (0 <= I <= n) and J (0 <= J <= min (i, m)).

Data range

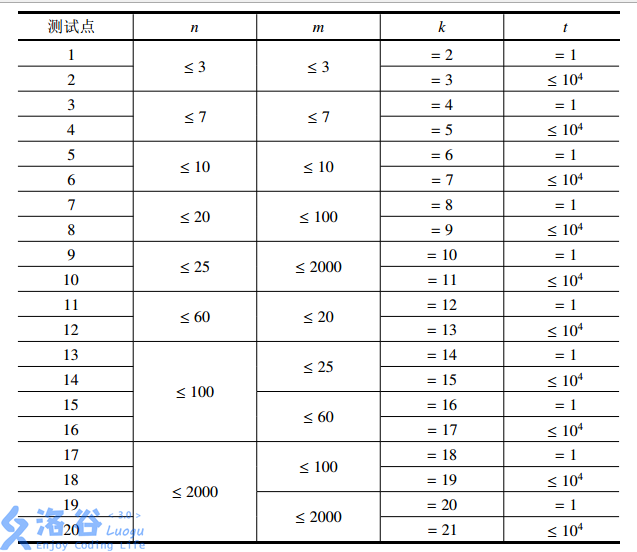
Approaches and Thoughts of Partial and Full Scores

30pts

Direct Violence Formula (without Yang Hui Triangle)

90pts

Yang Hui triangle + dichotomy.

Specific implementation: using vectorv [2005], the element J in V [i] makes (i,j) meet the requirements of J. Given n n n and m, then enumerate N and dichotomy M.

Code:

#include<bits/stdc++.h>
using namespace std;
int T,k,c[2005][2005];
vector<int>v[2005];
int main()
{
    scanf("%d %d",&T,&k);
    c[0][0]=c[1][0]=c[1][1]=1;
    for(int i=2;i<=2000;i++)
    {
        for(int j=0;j<=2000;j++)
        {
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
            if(c[i][j]%k==0) v[i].push_back(j);
        }
    }
    while(T--)
    {
        int n,m;
        scanf("%d %d",&n,&m);
        int ans=0;
        for(int i=2;i<=n;i++)
        {
            if(v[i].size()==0) continue;
            int endd=min(m,i);
            int l=0,r=v[i].size()-1,mid,tans=-1;
            while(l<=r)
            {
                mid=(l+r)/2;
                if(v[i][mid]>endd) r=mid-1;
                else l=mid+1,tans=mid;
            }
            ans+=tans+1;
        }
        printf("%d\n",ans);
    }
    return 0;
}

100pts

In fact, the above method can be A... on my computer. But there are two points on T in Luogu. I don't know about the chance of CCF Master.

The dichotomy is still too slow. Let's consider the pretreatment + O(1) method of answering each query: prefix and (two-dimensional)

How many groups of solutions satisfy the requirements when n=i and M = J are denoted by qian[i][j]. Very good. (r arrays are auxiliary arrays, r[i][j] denotes the one-dimensional prefix sum when n=i)

#include<bits/stdc++.h>
using namespace std;
int T,k,c[2005][2005],qian[2005][2005],r[2005][2005];
bool ok[2005][2005];
//vector<int>v[2005];
int main()
{
    scanf("%d %d",&T,&k);
    c[0][0]=c[1][0]=c[1][1]=1;
    for(int i=2;i<=2000;i++)
    {
        for(int j=0;j<=i;j++)
        {
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
            if(c[i][j]%k==0) ok[i][j]=1;
        }
    }
    for(int i=1;i<=2000;i++)
    {
        r[i][0]=ok[i][0];
        for(int j=1;j<=2000;j++)
        {
            r[i][j]=r[i][j-1]+ok[i][j];
        }
    }
    for(int i=1;i<=2000;i++)
    {
        for(int j=0;j<=2000;j++)
        {
            qian[i][j]=qian[i-1][j]+r[i][j];
        }
    }
    while(T--)
    {
        int n,m;
        scanf("%d %d",&n,&m);
        /*int ans=0;
        for(int i=2;i<=n;i++)
        {
            if(v[i].size()==0) continue;
            int endd=min(m,i);
            int l=0,r=v[i].size()-1,mid,tans=-1;
            while(l<=r)
            {
                mid=(l+r)/2;
                if(v[i][mid]>endd) r=mid-1;
                else l=mid+1,tans=mid;
            }
            ans+=tans+1;
        }*/
        printf("%d\n",qian[n][m>n?n:m]);
    }
    return 0;
}