This article modifies an error and adds a more detailed explanation to the article translated by Fu Huizhong (original author: Thomas Niemann).
introduction
Writing compilers was a very time-consuming task until 1975.This year Lesk[1975] and Johson [1975] published papers on lex and yacc.These tools greatly simplify writing compilers.Details on how to implement lex and yacc are described in Aho[1986].Wait until the lex and yacc tools are available from:
* Mortice Kern System (MKS), at www.mks.com,
** GNU flex and bison, at www.gnu.org,
* Ming, at www.mingw.org,
* Cygwin, at www.cygwin.org, and
* My Lex and Yacc versions, at epaperpress.com
The MKS version is a high-quality commercial product with a retail price of approximately $300.GNU software is free.The output data of flex can also be used by commercial versions, which correspond to a commercial version number of 1.24, as does bison.Ming and Cygwin are ports of GNU software on some 32-bit Windows systems.In fact, Cygwin is an analog interface on Windows for UNIX operating systems, including the gcc and g++ compilers.
* Figure 1: Compilation order
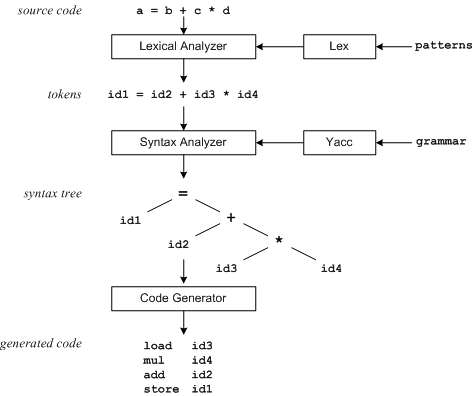
Lex generates C program code for a lexical analyzer or scanner.It matches the regular expressions to the input strings and converts them into corresponding tags.Tags are usually numeric values that represent strings or simple procedures.Figure 1 illustrates this.
When Lex finds specific tags in the input stream, it enters them into a specific symbol table.This symbol table also contains other information, such as the location of data types (integers or real numbers) and variables in memory.All instances of markup represent an appropriate index value in the symbol table.
Yacc generates C program code for a parser or parser.Yacc uses specific grammar rules to interpret tags derived from Lex and to generate a grammar tree.Grammar trees use various markers as hierarchical structures.For example, the prioritization and correlation of operators are evident in the grammar tree.Next, the compiler source code is generated, and the grammar tree is traversed once in the first depth to generate the source code.Some compilers generate machine code directly, and many more, such as the one shown above, output assemblers.
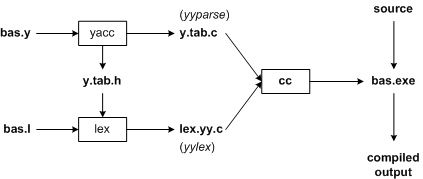
Figure 2: Build a compiler with Lex/Yacc
Figure 2 shows the naming conventions used by Lex and Yacc.Let's start by saying that our goal is to write a BASIC compiler.First we'l l specify all the pattern matching rules for Lex (bas.l) and all the syntax rules for Yacc (bas.y).The commands that generate our compiler, bas.exe, are listed below.
yacc -d bas.y # create y.tab.h, y.tab.c lex bas.l # create lex.yy.c cc lex.yy.c y.tab.c -obas.exe # compile/link
Yacc reads in the grammar description in bas.y and generates a parser, the function yyparse in y.tab.c.Bas.y contains a series of tag declarations.The'|d'option causes Yacc to generate tag declarations and save them in y.tab.c.Lex reads in the description of the regular expression in bas.l, including the file y.tab.h, and generates the lexical interpreter, the function y y Lex in the file lex.y Y.C.
Finally, the interpreter and the parser are connected to form an executable program, bas.exe.We call yyparse from the main function to run this compiler.The function yyparse automatically calls yylex to get each flag.
Lex
theory
In the first phase, the compiler reads in the source code and converts the string to the corresponding tag.Using regular expressions, we can design specific expressions for Lex to scan and match strings from input code.Each string corresponds to an action on Lex.Usually an action returns a tag representing a matched string for subsequent parsers to use.As a start of learning, here we don't return tags but simply print matched strings.We're going to use this regular expression below to scan for identifiers.letter(letter|digit)*The string matched by this problem expression starts with a simple character followed by zero or more characters or numbers.This is a good example of the operations allowed in regular expressions.
Repeat, indicated by'*'
Alternate, indicated by'|'
In series
Each regular expression represents a finite-state automaton (FSA).We can represent a FSA by transitions between States and states.This includes a start state and one or more end or acceptance states.
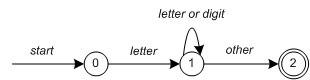
* Figure 3
State 0 is the start state and State 2 is the accept state in Figure 3.When a character is read in, we make a state transition.When the first letter is read in, the program transitions to state 1.If a letter or number is also read later, the program will remain in state 1.If the characters read in are not letters or numbers, the program transitions to state 2, which is the accepted state.Each FSA is represented as a computer program.For example, our 3-state machine is easier to implement:
start: goto state0 state0: read c if c = letter goto state1 goto state0 state1: read c if c = letter goto state1 if c = digit goto state1 goto state2 state2: accept string
This is the technology lex uses.Lex translates regular expressions into a computer program that simulates FSA.By searching a computer-generated status table, it is easy to determine the next status using the next input character and current status.Now we should be able to easily understand some of the limitations of lex.For example, Lex cannot be used to identify shell structures such as parentheses.A hybrid stack is required to identify the shell structure.When we encounter'('), we push it onto the stack.When we encounter')', we match it at the top of the stack and pop it up.However, Lex has only state and state transition capabilities.Because it has no stack, it is not suitable for profiling shell structures.yacc adds a stack to the FSA and can easily handle structures such as parentheses.It is important to use the appropriate tools for your specific work.Lex is good at pattern matching.yacc is suitable for more challenging work.
Practice
| Pattern | Matches |
|---|---|
| . | any character except newline |
| \. | literal . |
| \n | newline |
| \t | tab |
| ^ | beginning of line |
| $ | end of line |
Table 1: Simple pattern matching
| Pattern | Matches |
|---|---|
| ? | zero or one copy of the preceding expression |
| * | zero or more copies of the preceding expression |
| + | one or more copies of the preceding expression |
| a|b | a or b (alternating) |
| (ab)+ | one or more copies of ab (grouping) |
| abc | abc |
| abc* | ab abc abcc abccc ... |
| "abc*" | literal abc* |
| abc+ | abc abcc abccc abcccc ... |
| a(bc)+ | abc abcbc abcbcbc ... |
| a(bc)? | a abc |
Table 2: Example pattern matching
| Pattern | Matches |
|---|---|
| [abc] | one of: a b c |
| [a-z] | any letter a through z |
| [a\-z] | one of: a - z |
| [-az] | one of: - a z |
| [A-Za-z0-9]+ | one or more alphanumeric characters |
| [ \t\n]+ | whitespace |
| [^ab] | anything except: a b |
| [a^b] | one of: a ^ b |
| [a|b] | one of: a | b |
Table 3
Regular expressions in lex consist of ideographic characters (Table 1).Examples of pattern matching are listed in Table 2.In square brackets ([]), the usual operation loses its original meaning.Only two operations are retained in square brackets, a hyphen ('') and an accent ('^').When a hyphen is used between two characters, it indicates the range of the characters.When an accent is used in the start position, it reverses the following expression.If two patterns match the same string, the one with the longest matching length will be used.If the matching lengths are the same, the first listed paradigm is chosen.
...Define... %% ...rules... %% ...subroutine...
The input file for Lex is divided into three segments separated by%%.The above example illustrates this very well.The first example is the shortest available lex file:%%
The input characters will be output directly, one character at a time.Since there must be a rule segment, the first%% always requires it to exist.However, if we don't specify any rules, the default action is to match any characters and output them directly to the output file.The default input and output files are stdin and stdout, respectively.Here is an example of exactly the same effect, explicitly expressing the default code:
%% /* match everything except newline */ . ECHO; /* match newline */ \n ECHO; %% int yywrap(void) { return 1; } int main(void) { yylex(); return 0; }
Two paradigms are specified in the rule paragraph above.Each paradigm must start with the first column.It must be followed by a blank space (space, TAB, or line break) and any corresponding action.An action can be a single line of C code or a multiple line of C code enclosed in curly brackets.Any string that does not start from the first column is copied word by word into the resulting C file.We can use this special behavior to add comments to our lex files.In the example above, there are two paradigms'. 'and'\n', the corresponding actions are ECHO.Lex predefines some macros and variables.ECHO is a macro that directly outputs the characters matched by a pattern.This is also the default action for any unmatched characters.ECHO is usually defined as:
#define ECHO fwrite(yytext, yyleng, 1, yyout)
The variable yytext is a pointer (ending in NULL) to the matched string, and yyleng is the length of the string.The variable yyout is the output file and, by default, stdout.The function yywrap is called when Lex has read the input file.If 1 is returned, the program is finished, otherwise 0 is returned.Each C program requires a main function.In this case, we simply call the yylex, the entry to the lex scanner.Some Lex implementations include mains and yywraps in their libraries.That's why our first example, the shortest lex program, works correctly.
| Name | Function |
|---|---|
| int yylex(void) | call to invoke lexer, returns token |
| char *yytext | pointer to matched string |
| yyleng | length of matched string |
| yylval | value associated with token |
| int yywrap(void) | wrapup, return 1 if done, 0 if not done |
| FILE *yyout | output file |
| FILE *yyin | input file |
| INITIAL | initial start condition |
| BEGIN condition | switch start condition |
| ECHO | write matched string |
Below is a program that does nothing at all.All input characters are matched, but none of the paradigms define corresponding actions, so there is no output.
%% . \n
The following example inserts a line number before each line of a file.Some lex implementations predefine and compute yylineno variables.The input file is yyin, which points to stdin by default.
%{ int yylineno; %} %% ^(.*)\n printf("%4d\t%s", ++yylineno, yytext); %% int main(int argc, char *argv[]) { yyin = fopen(argv[1], "r"); yylex(); fclose(yyin); }
Definition segments consist of alternate, C-code, and start state.The C code in the definition section is simply copied to the top of the generated C file, and must be enclosed in%{and%}.Alternatives simplify regular expression rules.For example, we can define numbers and letters:
digit [0-9] letter [A-Za-z] %{ int count; %} %% /* match identifier */ {letter}({letter}|{digit})* count++; %% int main(void) { yylex(); printf("number of identifiers = %d\n", count); return 0; }
Paradigms and corresponding expressions must be separated by white space.In a rule paragraph, alternatives are enclosed in curly brackets (e.g. {letter}) to distinguish them from their literal meaning.Whenever a pattern is matched to a rule segment, the corresponding C code is run.Here is a scanner that calculates the number of characters, words and lines in a file (similar to wc programs in Unix):
%{ int nchar, nword, nline; %} %% \n { nline++; nchar++; } [^ \t\n]+ { nword++, nchar += yyleng; } . { nchar++; } %% int main(void) { yylex(); printf("%d\t%d\t%d\n", nchar, nword, nline); return 0; }
YACC
theory
The grammar of yacc is described by a variable that uses the BNF grammar (Backus_Naur form).The BNF grammar rules were originally invented by John Backus and Peter Naur and were used to describe the Algol60 language.BNF can be used to express context-independent languages.Most structures in modern programming languages can be expressed in BNF grammar.For example, the grammar for multiplying and adding values is:
1 E -> E + E 2 E -> E * E 3 E -> id
Three examples are given above, representing three rules (r1, r2, R3 in turn).A structure like E (expression) that appears on the left is called a nonterminal.Structures such as ID (identifier) are called terminators (terminal, the tag returned by lex), and they only appear on the right.This grammar indicates that an expression can be the sum, product or identifier of two expressions.We can use this grammar to construct the following expressions:
E -> E * E (r2) -> E * z (r3) -> E + E * z (r1) -> E + y * z (r3) -> x + y * z (r3)
At each step, we have extended a grammar structure, replacing the left with the corresponding right.The number on the right indicates which rule is applied.To parse an expression, we actually need to reverse the order.Instead of starting with a simple non-terminator and generating an expression from the grammar, the expression is progressively simplified to a non-terminator.This is called a "bottom-up" or "move-in-" reduction analysis, which requires a stack to hold the information.The following is a detailed description of the same syntax as the previous example in reverse order:
1 . x + y * z shift 2 x . + y * z reduce(r3) 3 E . + y * z shift 4 E + . y * z shift 5 E + y . * z reduce(r3) 6 E + E . * z shift 7 E + E * . z shift 8 E + E * z . reduce(r3) 9 E + E * E . reduce(r2) emit multiply 10 E + E . reduce(r1) emit add 11 E . accept
The structure to the left of the point is in the stack, and to the right of the point is the remaining input information.Let's start by moving the marker onto the stack.When the top and right tags of the stack match, we replace the matching tag with the left tag.Conceptually, the matching right tag is ejected from the stack, while the left tag is pushed into the stack.We think of the matched tag as a handle, and all we do is reduce the handle to the left.This process continues until all inputs are pushed into the stack, leaving only the initial non-terminators in the final stack.In Step 1, we pushed x onto the stack.Step 2 applies rule r3 to the stack to convert x to E.Then continue pushing and reducing until there is only a single non-terminator left in the stack, the start symbol.In step 9, we apply rule r2 to perform the multiplication instruction.Similarly, perform the addition command in step 10.In this case, multiplication has a higher priority than addition.Consider that if we do not continue pushing in at step 6, we apply rule r1 to the reduction immediately.This results in a higher priority for addition than for multiplication.This is called a shift reduce conflict.Our grammar is ambiguous, and more than one applicable rule can be referenced to an expression.In this case, the operator priority will work.As another example, you can imagine a rule like this:
E -> E + E
This is ambiguous because we can recurse from the left to the right.To save this crisis, we can rewrite grammar rules or give yacc instructions to prioritize operators.The latter method is simpler. We will demonstrate it in the exercise paragraph.
The following syntax has a reduce reduce conflict.When id is present in the stack, we can either classify it as T or E.
E -> T E -> id T -> id
In case of conflict, yacc will perform the default action.When there is a "move-in -" reduction conflict, yacc moves in.When there is a reduction conflict, yacc will execute the first rule listed.It displays warnings for any conflicts.Warning messages can only be extinguished by writing clear grammar rules.In the following sections, we will introduce some ways to eliminate ambiguity.
Exercise, Part One
...Define... %% ...rules... %% ...subroutine...
The input file for yacc is divided into three sections.The Definition section consists of a set of tag declarations and C code enclosed between'%{'and'%}'.The BNF syntax definition is placed in the Rules section, and the user subprogram is added in the Subprogram section.Constructing a small addition and subtraction calculator best illustrates this.We'll start by examining the link between lex and yacc.The following is the definition section of the yacc input file:
%token INTEGER
The above definition declares an INTEGER tag.When we run yacc, it generates a parser in y.tab.c and a file containing y.tab.h:
#ifndef YYSTYPE #define YYSTYPE int #endif #define INTEGER 258 extern YYSTYPE yylval;
The lex file should contain this header file and use its definition of the tag value.To get the tag, yacc calls yylex.The return value type of yylex is integer and can be used for return tags.The value corresponding to the returned tag is stored in the variable yylval.For example,
[09]+ { yylval = atoi(yytext); return INTEGER; }
The integer value is saved in yylval and the tag INTEGER is returned to yacc.The type of yylval is determined by YYSTYPE.Since its default type is integer, the program works fine in this example.The token value between 0 255 is conventionally a character value.For example, if you have such a rule
[+] return *yytext; /* Return Operator */
The character values of minus sign and plus sign will be returned.Note that we must put the minus sign first to avoid range assignment errors.Since lex also retains tag values such as End of File and Error Procedure, the resulting tag values usually start around 258.The following is a complete lex input file designed for our calculator:
%{ #include "y.tab.h" #include <stdlib.h> void yyerror(char *); %} %% [0-9]+ { yylval = atoi(yytext); return INTEGER; } [-+\n] return *yytext; [ \t] ; /* skip whitespace */ . yyerror("invalid character"); %% int yywrap(void) { return 1; }
Yacc maintains two stacks internally; an analysis stack and a content stack.Terminals and non-terminators are stored in the analysis stack and represent the current profiling state.The content stack is an array of YYSTYPE elements that hold a corresponding value for each element in the analysis stack.For example, when yylex returns an INTEGER tag, yacc moves the tag onto the analysis stack.At the same time, the corresponding yylval value will be moved into the content stack.The contents of the analysis stack and the content stack are always synchronized, so it is easy to find a value corresponding to a tag from the stack.Here is the yacc input file designed for my calculator:
%{ #include <stdio.h> int yylex(void); void yyerror(char *); %} %token INTEGER %% program: program expr '\n' { printf("%d\n", $2); } | ; expr: INTEGER { $$ = $1; } | expr '+' expr { $$ = $1 + $3; } | expr '-' expr { $$ = $1 - $3; } ; %% void yyerror(char *s) { fprintf(stderr, "%s\n", s); } int main(void) { yyparse(); return 0; }
The method of the rule segment is similar to the BNF grammar discussed earlier.The first rule is called the command rule.The left, or non-terminator, starts from the far left, followed by a clone of its own.Following it is the right style.The action corresponding to the rule is written in curly brackets at the end.
By using left recursion, we have specified that a program consists of 0 or more expressions.Each expression ends with a line break.When a line break is detected, the program prints the result of the expression.When the program applies the following rule
expr: expr '+' expr { $$ = $1 + $3; }
In the analysis stack, we actually use left instead of right.In this example, we pop up "expr'+'expr" and press "expr".We push one member down the reduced stack by ejecting three members.Values in the content stack can be accessed through relative addresses in our C code,'$1'for the first member in the right style,'$2' for the second, and so on."$$" denotes the top of the reduced stack.In the above action, the values of the corresponding two expressions are added together, three members of the content stack are popped up, and the resulting and pushed into the stack.In this way, the contents in the analysis and content stacks are still synchronized.
When we reduce INTEGER to expr, numeric values begin to be entered into the content stack.We will apply this rule when NTEGER is moved into the analysis stack
expr: INTEGER { $$ = $1; }
The INTEGER tag is ejected from the analysis stack and pushed into an expr.For the content stack, we pop up the integer value and push it back.Or, we didn't do anything.In fact, this is the default action and does not need to be specified.When a line break is encountered, the value corresponding to expr is printed.When a syntax error is encountered, yacc calls the user-provided yyerror function.If you need to modify the calling interface for yyerror, change the shell file contained in yacc to suit your needs.The last function in your yacc file is main... in case you wonder where it is.This example still has ambiguous grammar.Yacc will display the "move in -" reduction warning, but will still be able to handle the grammar with the default move in operation.
Exercise, Part Two
In this paragraph, we'll expand the calculator in the previous paragraph to include some new features.New features include arithmetic multiplication and division.Parentheses can be used to change the priority of operations, and the values of single-character variables can be defined externally.The following examples illustrate the inputs and the output of the calculator:
user: 3 * (4 + 5) calc: 27 user: x = 3 * (4 + 5) user: y = 5 user: x calc: 27 user: y calc: 5 user: x + 2*y calc: 37
The vocabulary interpreter will return the VARIABLE and INTEGER flags.For variables, yylval specifies an index into our symbol table sym.For this program, sym only holds the value of the corresponding variable.When the INTEGER flag is returned, yylval saves the scanned value.Here is the lex input file:
%{ #include <stdlib.h> #include "y.tab.h" void yyerror(char *); %} %% /* variables */ [a-z] { yylval = *yytext - 'a'; return VARIABLE; } /* integers */ [0-9]+ { yylval = atoi(yytext); return INTEGER; } /* operators */ [-+()=/*\n] { return *yytext; } /* skip whitespace */ [ \t] ; /* anything else is an error */ . yyerror("invalid character"); %% int yywrap(void) { return 1; }
Following is the input file for yacc.Yacc uses the tags of INTEGER and VARIABLE to generate #defines in y.tab.h for use in lex.This follows the definition of the arithmetic operator.We can specify%left for left binding or%right for right binding.The definitions listed at the end have the highest priority.Multiplication and division therefore have higher priority than addition and subtraction.All four arithmetic operators are left-joined.With this simple technique, we can eliminate grammatical ambiguity.
%token INTEGER VARIABLE %left '+' '-' %left '*' '/' %{ void yyerror(char *); int yylex(void); int sym[26]; %} %% program: program statement '\n' | ; statement: expr { printf("%d\n", $1); } | VARIABLE '=' expr { sym[$1] = $3; } ; expr: INTEGER | VARIABLE { $$ = sym[$1]; } | expr '+' expr { $$ = $1 + $3; } | expr '-' expr { $$ = $1 - $3; } | expr '*' expr { $$ = $1 * $3; } | expr '/' expr { $$ = $1 / $3; } | '(' expr ')' { $$ = $2; } ; %% void yyerror(char *s) { fprintf(stderr, "%s\n", s); } int main(void) { yyparse(); return 0; }
Calculator
describe
This version of the calculator is much more complex than the previous version.Major changes include control structures such as if_else and while.In addition, a grammar tree is constructed during the parsing process.After the parsing is complete, we traverse the grammar tree to generate the output.Two versions of tree traversal are provided here:
* An interpreter that executes the declarations in the tree during tree traversal, and
* A compiler that generates code for a stack-based computer.There is a routine here to make our interpretation more visible.
x = 0; while (x < 3) { print x; x = x + 1; }
Explain version output data:
0 1 2
Compiled version output data:
push 0 pop x L000: push x push 3 compLT jz L001 push x print push x push 1 add pop x jmp L000 L001:
Version output for generating grammar trees:
[=]
|
|----|
| |
id(X) c(0)
Graph 1:
while
|
|----------------|
| |
[<] [;]
| |
|----| |----------|
| | | |
id(X) c(3) print [=]
| |
| |-------|
| | |
id(X) id(X) [+]
|
|----|
| |
id(X) c(1)
Includes definitions of grammar trees and symbol tables.Symbol table sym allows variable names to be represented by a single character.Each node in the grammar tree holds a constant (conNodeType), an identifier (idNodeType), or an internal node with an operator (oprNodeType).All three variables are compressed in a union structure, and the specific type of node is determined by the structure it has inside.
The lex input file contains regular expressions that return the VARIABLE and INTEGER flags.In addition, the flags of double-character operators such as EQ and NE are defined.For a single-character operator, simply return to itself.
The yacc input file defines the type of YYSTYPE, yylval, as follows
%union { int iValue; /* integer value */ char sIndex; /* symbol table index */ nodeType *nPtr; /* node pointer */ };
This will result in the following code being generated in y.tab.h:
typedef union { int iValue; /* integer value */ char sIndex; /* symbol table index */ nodeType *nPtr; /* node pointer */ } YYSTYPE; extern YYSTYPE yylval;
Constants, variables, and nodes can all be represented by yylval s in the parser's content stack.
0 { yylval.iValue = atoi(yytext); return INTEGER; } [1-9][0-9]* { yylval.iValue = atoi(yytext); return INTEGER; }
Note the following definitions:
%token <iValue> INTEGER %type <nPtr> expr
This binds expr and INTEGER to nPtr and iValue members in the union structure YYSTYPE, respectively.This is required so that yacc can generate the correct code.For example, this rule:
expr: INTEGER { $$ = con($1); }
The following code can be generated.Note that y yyvsp[0] represents the top of the content stack or the value corresponding to INTEGER.
yylval.nPtr = con(yyvsp[0].iValue);
A unary operator has a higher priority than a binary operator, as shown below:
%left GE LE EQ NE '>' '<' %left '+' '-' %left '*' '/' %nonassoc UMINUS
%nonassoc means there is no dependency.It is often used in conjunctions with%prec to specify the priority of a rule.So we can do this:
expr: '' expr %prec UMINUS { $$ = node(UMINUS, 1, $2); }
* Indicates that this rule has the same priority as the flag UMINUS.Moreover, as defined above, UMINUS has a higher priority than all other operators.Similar techniques are used to eliminate ambiguity in if else structures (see if else ambiguity).
The grammar tree is constructed from the bottom up, allocating leaf nodes when variables and integers are reduced.When an operator is encountered, a node needs to be assigned and the last assigned node recorded as an operand.
After the grammar tree is constructed, call function ex to do the first deep traversal of the grammar tree.The first depth traversal visits each node in the order in which it was originally assigned.
This will result in each operator being used in the order in which it was accessed during profiling.There are three versions of the ex function: an interpreted version, a compiled version, and a version used to generate the grammar tree.
Include file
typedef enum { typeCon, typeId, typeOpr } nodeEnum; /* constants */ typedef struct { int value; /* value of constant */ } conNodeType; /* identifiers */ typedef struct { int i; /* subscript to sym array */ } idNodeType; /* operators */ typedef struct { int oper; /* operator */ int nops; /* number of operands */ struct nodeTypeTag *op[1]; /* operands, extended at runtime */ } oprNodeType; typedef struct nodeTypeTag { nodeEnum type; /* type of node */ union { conNodeType con; /* constants */ idNodeType id; /* identifiers */ oprNodeType opr; /* operators */ }; } nodeType; extern int sym[26];
Lex input file
%{ #include <stdlib.h> #include "calc3.h" #include "y.tab.h" void yyerror(char *); %} %% [a-z] { yylval.sIndex = *yytext - 'a'; return VARIABLE; } 0 { yylval.iValue = atoi(yytext); return INTEGER; } [1-9][0-9]* { yylval.iValue = atoi(yytext); return INTEGER; } [-()<>=+*/;{}.] { return *yytext; } ">=" return GE; "<=" return LE; "==" return EQ; "!=" return NE; "while" return WHILE; "if" return IF; "else" return ELSE; "print" return PRINT; [ \t\n]+ ; /* ignore whitespace */ . yyerror("Unknown character"); %% int yywrap(void) { return 1; }
Yacc Input File
%{ #include <stdio.h> #include <stdlib.h> #include <stdarg.h> #include "calc3.h" /* prototypes */ nodeType *opr(int oper, int nops, ...); nodeType *id(int i); nodeType *con(int value); void freeNode(nodeType *p); int ex(nodeType *p); int yylex(void); void yyerror(char *s); int sym[26]; /* symbol table */ %} %union { int iValue; /* integer value */ char sIndex; /* symbol table index */ nodeType *nPtr; /* node pointer */ }; %token <iValue> INTEGER %token <sIndex> VARIABLE %token WHILE IF PRINT %nonassoc IFX %nonassoc ELSE %left GE LE EQ NE '>' '<' %left '+' '-' %left '*' '/' %nonassoc UMINUS %type <nPtr> stmt expr stmt_list %% program: function { exit(0); } ; function: function stmt { ex($2); freeNode($2); } | /* NULL */ ; stmt: ';' { $$ = opr(';', 2, NULL, NULL); } | expr ';' { $$ = $1; } | PRINT expr ';' { $$ = opr(PRINT, 1, $2); } | VARIABLE '=' expr ';' { $$ = opr('=', 2, id($1), $3); } | WHILE '(' expr ')' stmt { $$ = opr(WHILE, 2, $3, $5); } | IF '(' expr ')' stmt %prec IFX { $$ = opr(IF, 2, $3, $5); } | IF '(' expr ')' stmt ELSE stmt { $$ = opr(IF, 3, $3, $5, $7); } | '{' stmt_list '}' { $$ = $2; } ; stmt_list: stmt { $$ = $1; } | stmt_list stmt { $$ = opr(';', 2, $1, $2); } ; expr: INTEGER { $$ = con($1); } | VARIABLE { $$ = id($1); } | '-' expr %prec UMINUS { $$ = opr(UMINUS, 1, $2); } | expr '+' expr { $$ = opr('+', 2, $1, $3); } | expr '-' expr { $$ = opr('-', 2, $1, $3); } | expr '*' expr { $$ = opr('*', 2, $1, $3); } | expr '/' expr { $$ = opr('/', 2, $1, $3); } | expr '<' expr { $$ = opr('<', 2, $1, $3); } | expr '>' expr { $$ = opr('>', 2, $1, $3); } | expr GE expr { $$ = opr(GE, 2, $1, $3); } | expr LE expr { $$ = opr(LE, 2, $1, $3); } | expr NE expr { $$ = opr(NE, 2, $1, $3); } | expr EQ expr { $$ = opr(EQ, 2, $1, $3); } | '(' expr ')' { $$ = $2; } ; %% nodeType *con(int value) { nodeType *p; /* allocate node */ if ((p = malloc(sizeof(nodeType))) == NULL) yyerror("out of memory"); /* copy information */ p->type = typeCon; p->con.value = value; return p; } nodeType *id(int i) { nodeType *p; /* allocate node */ if ((p = malloc(sizeof(nodeType))) == NULL) yyerror("out of memory"); /* copy information */ p->type = typeId; p->id.i = i; return p; } nodeType *opr(int oper, int nops, ...) { va_list ap; nodeType *p; int i; /* allocate node, extending op array */ if ((p = malloc(sizeof(nodeType) + (nops-1) * sizeof(nodeType *))) == NULL) yyerror("out of memory"); /* copy information */ p->type = typeOpr; p->opr.oper = oper; p->opr.nops = nops; va_start(ap, nops); for (i = 0; i < nops; i++) p->opr.op[i] = va_arg(ap, nodeType*); va_end(ap); return p; } void freeNode(nodeType *p) { int i; if (!p) return; if (p->type == typeOpr) { for (i = 0; i < p->opr.nops; i++) freeNode(p->opr.op[i]); } free (p); } void yyerror(char *s) { fprintf(stdout, "%s\n", s); } int main(void) { yyparse(); return 0; }
Interpreter Version
#include <stdio.h> #include "calc3.h" #include "y.tab.h" int ex(nodeType *p) { if (!p) return 0; switch(p->type) { case typeCon: return p->con.value; case typeId: return sym[p->id.i]; case typeOpr: switch(p->opr.oper) { case WHILE: while(ex(p->opr.op[0])) ex(p->opr.op[1]); return 0; case IF: if (ex(p->opr.op[0])) ex(p->opr.op[1]); else if (p->opr.nops > 2) ex(p->opr.op[2]); return 0; case PRINT: printf("%d\n", ex(p->opr.op[0])); return 0; case ';': ex(p->opr.op[0]); return ex(p->opr.op[1]); case '=': return sym[p->opr.op[0]->id.i] = ex(p->opr.op[1]); case UMINUS: return -ex(p->opr.op[0]); case '+': return ex(p->opr.op[0]) + ex(p->opr.op[1]); case '-': return ex(p->opr.op[0]) - ex(p->opr.op[1]); case '*': return ex(p->opr.op[0]) * ex(p->opr.op[1]); case '/': return ex(p->opr.op[0]) / ex(p->opr.op[1]); case '<': return ex(p->opr.op[0]) < ex(p->opr.op[1]); case '>': return ex(p->opr.op[0]) > ex(p->opr.op[1]); case GE: return ex(p->opr.op[0]) >= ex(p->opr.op[1]); case LE: return ex(p->opr.op[0]) <= ex(p->opr.op[1]); case NE: return ex(p->opr.op[0]) != ex(p->opr.op[1]); case EQ: return ex(p->opr.op[0]) == ex(p->opr.op[1]); } } return 0; }
Compiler Version
#include <stdio.h> #include "calc3.h" #include "y.tab.h" static int lbl; int ex(nodeType *p) { int lbl1, lbl2; if (!p) return 0; switch(p->type) { case typeCon: printf("\tpush\t%d\n", p->con.value); break; case typeId: printf("\tpush\t%c\n", p->id.i + 'a'); break; case typeOpr: switch(p->opr.oper) { case WHILE: printf("L%03d:\n", lbl1 = lbl++); ex(p->opr.op[0]); printf("\tjz\tL%03d\n", lbl2 = lbl++); ex(p->opr.op[1]); printf("\tjmp\tL%03d\n", lbl1); printf("L%03d:\n", lbl2); break; case IF: ex(p->opr.op[0]); if (p->opr.nops > 2) { /* if else */ printf("\tjz\tL%03d\n", lbl1 = lbl++); ex(p->opr.op[1]); printf("\tjmp\tL%03d\n", lbl2 = lbl++); printf("L%03d:\n", lbl1); ex(p->opr.op[2]); printf("L%03d:\n", lbl2); } else { /* if */ printf("\tjz\tL%03d\n", lbl1 = lbl++); ex(p->opr.op[1]); printf("L%03d:\n", lbl1); } break; case PRINT: ex(p->opr.op[0]); printf("\tprint\n"); break; case '=': ex(p->opr.op[1]); printf("\tpop\t%c\n", p->opr.op[0]->id.i + 'a'); break; case UMINUS: ex(p->opr.op[0]); printf("\tneg\n"); break; default: ex(p->opr.op[0]); ex(p->opr.op[1]); switch(p->opr.oper) { case '+': printf("\tadd\n"); break; case '-': printf("\tsub\n"); break; case '*': printf("\tmul\n"); break; case '/': printf("\tdiv\n"); break; case '<': printf("\tcompLT\n"); break; case '>': printf("\tcompGT\n"); break; case GE: printf("\tcompGE\n"); break; case LE: printf("\tcompLE\n"); break; case NE: printf("\tcompNE\n"); break; case EQ: printf("\tcompEQ\n"); break; } } } return 0; }
AST Abstract Grammar Tree Version
/* source code courtesy of Frank Thomas Braun */ /* Generation of the graph of the syntax tree */ #include <stdio.h> #include <string.h> #include <stdlib.h> #include "calc3.h" #include "y.tab.h" int del = 1; /* distance of graph columns */ int eps = 3; /* distance of graph lines */ /* interface for drawing (can be replaced by "real" graphic using GD or other) */ void graphInit (void); void graphFinish(); void graphBox (char *s, int *w, int *h); void graphDrawBox (char *s, int c, int l); void graphDrawArrow (int c1, int l1, int c2, int l2); /* recursive drawing of the syntax tree */ void exNode (nodeType *p, int c, int l, int *ce, int *cm); /*****************************************************************************/ /* main entry point of the manipulation of the syntax tree */ int ex (nodeType *p) { int rte, rtm; graphInit (); exNode (p, 0, 0, &rte, &rtm); graphFinish(); return 0; } /*c----cm---ce----> drawing of leaf-nodes l leaf-info */ /*c---------------cm--------------ce----> drawing of non-leaf-nodes l node-info * | * ------------- ...---- * | | | * v v v * child1 child2 ... child-n * che che che *cs cs cs cs * */ void exNode ( nodeType *p, int c, int l, /* start column and line of node */ int *ce, int *cm /* resulting end column and mid of node */ ) { int w, h; /* node width and height */ char *s; /* node text */ int cbar; /* "real" start column of node (centred above subnodes) */ int k; /* child number */ int che, chm; /* end column and mid of children */ int cs; /* start column of children */ char word[20]; /* extended node text */ if (!p) return; strcpy (word, "???"); /* should never appear */ s = word; switch(p->type) { case typeCon: sprintf (word, "c(%d)", p->con.value); break; case typeId: sprintf (word, "id(%c)", p->id.i + 'A'); break; case typeOpr: switch(p->opr.oper){ case WHILE: s = "while"; break; case IF: s = "if"; break; case PRINT: s = "print"; break; case ';': s = "[;]"; break; case '=': s = "[=]"; break; case UMINUS: s = "[_]"; break; case '+': s = "[+]"; break; case '-': s = "[-]"; break; case '*': s = "[*]"; break; case '/': s = "[/]"; break; case '<': s = "[<]"; break; case '>': s = "[>]"; break; case GE: s = "[>=]"; break; case LE: s = "[<=]"; break; case NE: s = "[!=]"; break; case EQ: s = "[==]"; break; } break; } /* construct node text box */ graphBox (s, &w, &h); cbar = c; *ce = c + w; *cm = c + w / 2; /* node is leaf */ if (p->type == typeCon || p->type == typeId || p->opr.nops == 0) { graphDrawBox (s, cbar, l); return; } /* node has children */ cs = c; for (k = 0; k < p->opr.nops; k++) { exNode (p->opr.op[k], cs, l+h+eps, &che, &chm); cs = che; } /* total node width */ if (w < che - c) { cbar += (che - c - w) / 2; *ce = che; *cm = (c + che) / 2; } /* draw node */ graphDrawBox (s, cbar, l); /* draw arrows (not optimal: children are drawn a second time) */ cs = c; for (k = 0; k < p->opr.nops; k++) { exNode (p->opr.op[k], cs, l+h+eps, &che, &chm); graphDrawArrow (*cm, l+h, chm, l+h+eps-1); cs = che; } } /* interface for drawing */ #define lmax 200 #define cmax 200 char graph[lmax][cmax]; /* array for ASCII-Graphic */ int graphNumber = 0; void graphTest (int l, int c) { int ok; ok = 1; if (l < 0) ok = 0; if (l >= lmax) ok = 0; if (c < 0) ok = 0; if (c >= cmax) ok = 0; if (ok) return; printf ("\n+++error: l=%d, c=%d not in drawing rectangle 0, 0 ... %d, %d", l, c, lmax, cmax); exit(1); } void graphInit (void) { int i, j; for (i = 0; i < lmax; i++) { for (j = 0; j < cmax; j++) { graph[i][j] = ' '; } } } void graphFinish() { int i, j; for (i = 0; i < lmax; i++) { for (j = cmax-1; j > 0 && graph[i][j] == ' '; j--); graph[i][cmax-1] = 0; if (j < cmax-1) graph[i][j+1] = 0; if (graph[i][j] == ' ') graph[i][j] = 0; } for (i = lmax-1; i > 0 && graph[i][0] == 0; i--); printf ("\n\nGraph %d:\n", graphNumber++); for (j = 0; j <= i; j++) printf ("\n%s", graph[j]); printf("\n"); } void graphBox (char *s, int *w, int *h) { *w = strlen (s) + del; *h = 1; } void graphDrawBox (char *s, int c, int l) { int i; graphTest (l, c+strlen(s)-1+del); for (i = 0; i < strlen (s); i++) { graph[l][c+i+del] = s[i]; } } void graphDrawArrow (int c1, int l1, int c2, int l2) { int m; graphTest (l1, c1); graphTest (l2, c2); m = (l1 + l2) / 2; while (l1 != m) { graph[l1][c1] = '|'; if (l1 < l2) l1++; else l1--; } while (c1 != c2) { graph[l1][c1] = '-'; if (c1 < c2) c1++; else c1--; } while (l1 != l2) { graph[l1][c1] = '|'; if (l1 < l2) l1++; else l1--; } graph[l1][c1] = '|'; }
Reference resources
http://sighingnow.github.io/%E7%BC%96%E8%AF%91%E5%8E%9F%E7%90%86/bnf.html