I will go against my instinct, disobey my nature and love you forever.

Let's summarize the sorting (left over from the last lesson)

1, Stability of sorting (02:56)
The same values in the sorting process are sorted by the sorting algorithm, and their relative order remains unchanged.
(for the simple basic type array, it is of little use. It doesn't matter that 3 and 3 are 3). However, if you sort according to two indicators, you can get that the students in classes 1 to 10 are sorted by age to get the high-quality and cheap products in the website

Select sort (unstable)
33331333
First find 1 and exchange the first 3. The first 3 ran to the back
Bubble sorting (stable)
6 5 4 5 3 4 6
When two adjacent numbers are compared, they can remain stable without exchanging the order when they are equal
Insert sort (stable)
3 2 2 —
When comparing the numbers on the right, if they are equal, stop at this position to achieve stability
Merge sort (stable)
Merge is the key. When two groups merge, when comparing the left and right numbers, they appear equal. First merge the left one to achieve stability
Fast exhaust (unstable)
Not at the party
6 7 6 6 3
Take 5 as the division value, look at the next 6, look at the next 7, look at the next 6, look at the next 6, look at 3, which is smaller than 5. Directly exchange 3 and the first 6, resulting in instability
Heap sort (unstable)
5 4 4 6
When building a heap, it is easy to exchange numbers, resulting in the destruction of stability
Bucket sort and cardinality sort (stable)
Sorting without comparison is easy to keep the relative order unchanged
This can be achieved as long as the relative order in the bucket is maintained.

2, Summary (21:03)
According to the three dimensions of time complexity, space complexity and stability

algorithm	Time complexity	Spatial complexity	stability
Select sort	O(N^2)	O(1)	NO
Bubbling	O(N^2)	O(1)	YES
insert	O(N^2)	O(1)	YES
Merge	O(N*logN)	O(N)	YES
Random fast scheduling	O(N*logN)	O(logN)	NO
Heap sort	O(N*logN)	O(1)	NO

(1) Comparison based sorting cannot achieve time complexity below O(NlogN)
(2) If the time complexity is O(NlogN), the stability cannot be guaranteed if the space complexity is below O(N).

So:
Fast platoon is the fastest;
Stack when space is limited;
Stability needs to be merged.

Big hole in interview:
Odd numbers are placed on the left of the array and even numbers are placed on the right of the array. When it is stable, O (N) is empty. Can o (1)?
No, the partition of the classic fast platoon can't be stable, but the partition of the classic fast platoon is a 0-1 standard and an adjustment strategy in this problem, so the fast platoon can't be done, so it can't.

Improvement of algorithm in Engineering
(1) Make full use of the advantages of O(NlogN) and O(N^2)
The overall scheduling uses the idea of fast scheduling, but for the sorting of small sample size, the interpolation method with very low constant time is adopted
In sorting, make full use of the advantages of O(NlogN) and O(N^2)

(2) Consider stability
For basic types, the sorting strategy with faster speed regardless of stability will be used, but once non basic types appear, the algorithm strategy considering stability will be used to consider stability

PS: in the sorting methods provided in many programming languages, this comprehensive sorting method will be used to write sorting (in order to make full use of the advantages of each algorithm and maximize the sorting performance of the language)

3, Hash table and ordered table (44:37)

What is the difference between Set and Map?
Map: key–>value
Set: key

1. Hash table
In C + +, it is called unordered map / unordered map and unordered set / unordered set
In Java, it is called HashSet and HashMap

hashSet1 of key Is the base type->int Type (passed by value. For the basic type, the occupied space is the size of the stored thing itself)

HashSet <Integer> hashSet1 = new HashSet<>();
hashSet1.add(1);//increase
System.out.println(hashSet1.contains(1));//Check (whether 1 is the key in the output haspset)
//Output result: true
hashSet1.remove(1);//Delete
System.out.println(hashSet1.contains(1));
//Output result: false


//hashMap
HashMap <Integer,String> mapTest = new HashMap<>();
mapTest.put(1,"meng");//increase
System.out.println(mapTest.containsKey(1));//Check whether this key exists
//Output result: true
System.out.println(mapTest.get(1));//Check the value corresponding to this key
//Output result: meng
mapTest.put(1,"fan")；//When the stored key already exists, adding is changing
System.out.println(mapTest.get(1));//Check the value corresponding to this key
//Output result: fan
mapTest.remove(1);//Delete the key value pair with key = 1, and the value will disappear together
System.out.println(mapTest.get(1));
Output results://null

When the hash table is used, it is considered that all addition, deletion, modification and query operations are constant level, but this constant is larger than array direct addressing

// The key of hashSet2 is non basic type - > Node type (passed by reference, the value stored in the hash table is the address of the thing to be placed. At this time, the size of the hash table is not affected by the Node. The Node is large, and it is only an 8-byte address in the hash table)
		nodeA = new Node(1)；//This 1 is an attribute stored in the Node node
		nodeB = new Node(1);
		HashSet<Node> hashSet2 = new HashSet<>();
		hashSet2.add(nodeA);//increase
//Assuming that the address of NodeA is 0x1122, 0x1122 is stored in the hash table
		System.out.println(hashSet2.contains(nodeA));//Check whether the value exists
		//Output result: true
		System.out.println(hashSet2.contains(nodeB));
		//Output result: false
		hashSet2.remove(nodeA);//Delete
		System.out.println(hashSet2.contains(nodeA));
		//Output result: false

2. Ordered table (58:50)
In C + +, it is called OrderedMap/SortedMap and OrderedSet/SortedSet
It is called TreeMap and TreeSet in Java

//The ordered table is organized in order according to the Key, which is better than HashMap. HashMap can do everything TreeMap can do, and it will have more functions

TreeMap<Integer, String> treeMap1 = new TreeMap<>();//This type of key is a basic type, which can naturally compare sizes. If you use a non basic type as a key, you need to add a comparator and pass it by value
		treeMap1.put(7, "I'm 7");//put and hash table are both addition and modification
		treeMap1.put(5, "I'm 5");
		treeMap1.put(4, "I'm 4");
		treeMap1.put(3, "I'm 3");
		treeMap1.put(9, "I'm 9");
		treeMap1.put(2, "I'm 2");
		System.out.println(treeMap1.containsKey(5));//Same as hash table
		System.out.println(treeMap1.get(5));
		System.out.println(treeMap1.firstKey() + ", My youngest");//Because it is organized in order, the smallest one can be found
		System.out.println(treeMap1.lastKey() + ", My biggest");//You can also find the biggest
		System.out.println(treeMap1.floorKey(8) + ", All in table<=8 Of the numbers, I'm closest to 8");//Can find the nearest one less than or equal to
		System.out.println(treeMap1.ceilingKey(8) + ", All in table>=8 Of the numbers, I'm closest to 8");//Can find the nearest one greater than or equal to
		System.out.println(treeMap1.floorKey(7) + ", All in table<=7 Of the numbers, I'm closest to 7");
		System.out.println(treeMap1.ceilingKey(7) + ", All in table>=7 Of the numbers, I'm closest to 7");
		treeMap1.remove(5);//Can delete
		System.out.println(treeMap1.get(5) + ", If you delete it, it's gone");

When the ordered table is used, the operation is at the O (logN) level (which is also very good)

4, Single linked list and double linked list (1:10:10)
In the linked list title, if there is an operation involving head change, the return value is required. If there is no head change operation, the return value is not required

Simple example:
Print the common part of the ordered linked list: two pointers point to one end of the linked list (taking the minimum start as an example), and compare
The element indicated by the pointer moves to the next small one, prints equally, and moves to the next one at the same time until one is out of bounds

Linked list problem solving methodology (1:15:24)
Thoughts on questions in written examination and interview:
Written examination is all about time complexity;
Interview time complexity comes first, and find the most space-saving method

Key skills:
(1) Additional data structure records
(2) Speed pointer

Judge whether the linked list is palindrome structure (1:17:44)
Written examination stack, first in, last out, compare one by one (only the right half can be compared with the left one by one)
How do you know it's half done?
Speed pointer:
The fast pointer takes two steps at a time, and the slow pointer takes one step at a time. When the fast pointer is finished, the slow pointer is just half

// need n extra space
	public static boolean isPalindrome1(Node head) {
		Stack<Node> stack = new Stack<Node>();
		Node cur = head;
		while (cur != null) {
			stack.push(cur);
			cur = cur.next;
		}
		while (head != null) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

// need n/2 extra space
	public static boolean isPalindrome2(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node right = head.next;
		Node cur = head;
		while (cur.next != null && cur.next.next != null) {
			right = right.next;
			cur = cur.next.next;
		}
		Stack<Node> stack = new Stack<Node>();
		while (right != null) {
			stack.push(right);
			right = right.next;
		}
		while (!stack.isEmpty()) {
			if (head.value != stack.pop().value) {
				return false;
			}
			head = head.next;
		}
		return true;
	}

interview:

Temporarily change the linked list to

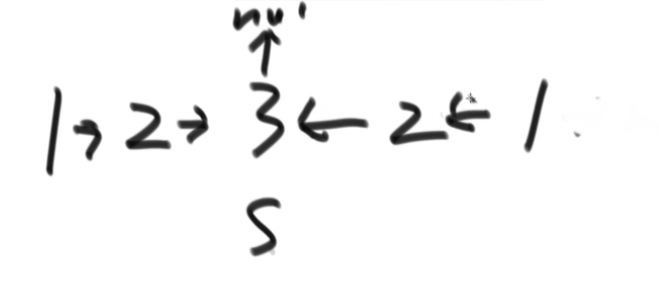
Then the two pointers remember that the head and tail move to the middle and compare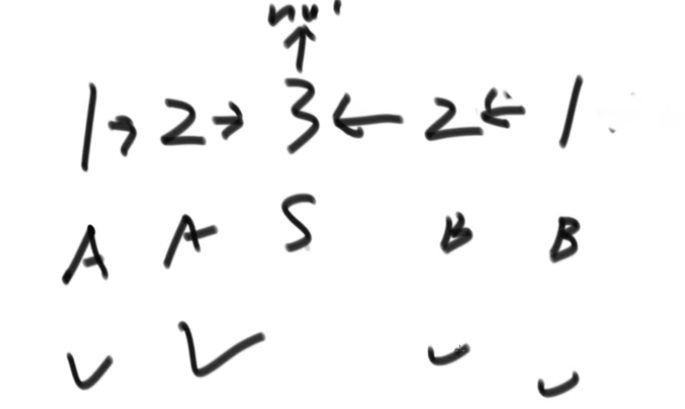In the end, one is empty and stops. If each step is the same, it is palindrome,
Restore the linked list before returning;

// need O(1) extra space
	public static boolean isPalindrome3(Node head) {
		if (head == null || head.next == null) {
			return true;
		}
		Node n1 = head;
		Node n2 = head;
		while (n2.next != null && n2.next.next != null) { // find mid node
			n1 = n1.next; // n1 -> mid
			n2 = n2.next.next; // n2 -> end
		}
		n2 = n1.next; // n2 -> right part first node
		n1.next = null; // mid.next -> null
		Node n3 = null;
		while (n2 != null) { // right part convert
			n3 = n2.next; // n3 -> save next node
			n2.next = n1; // next of right node convert
			n1 = n2; // n1 move
			n2 = n3; // n2 move
		}
		n3 = n1; // n3 -> save last node
		n2 = head;// n2 -> left first node
		boolean res = true;
		while (n1 != null && n2 != null) { // check palindrome
			if (n1.value != n2.value) {
				res = false;
				break;
			}
			n1 = n1.next; // left to mid
			n2 = n2.next; // right to mid
		}
		n1 = n3.next;
		n3.next = null;
		while (n1 != null) { // recover list
			n2 = n1.next;
			n1.next = n3;
			n3 = n1;
			n1 = n2;
		}
		return res;
	}

Look at the code!!!

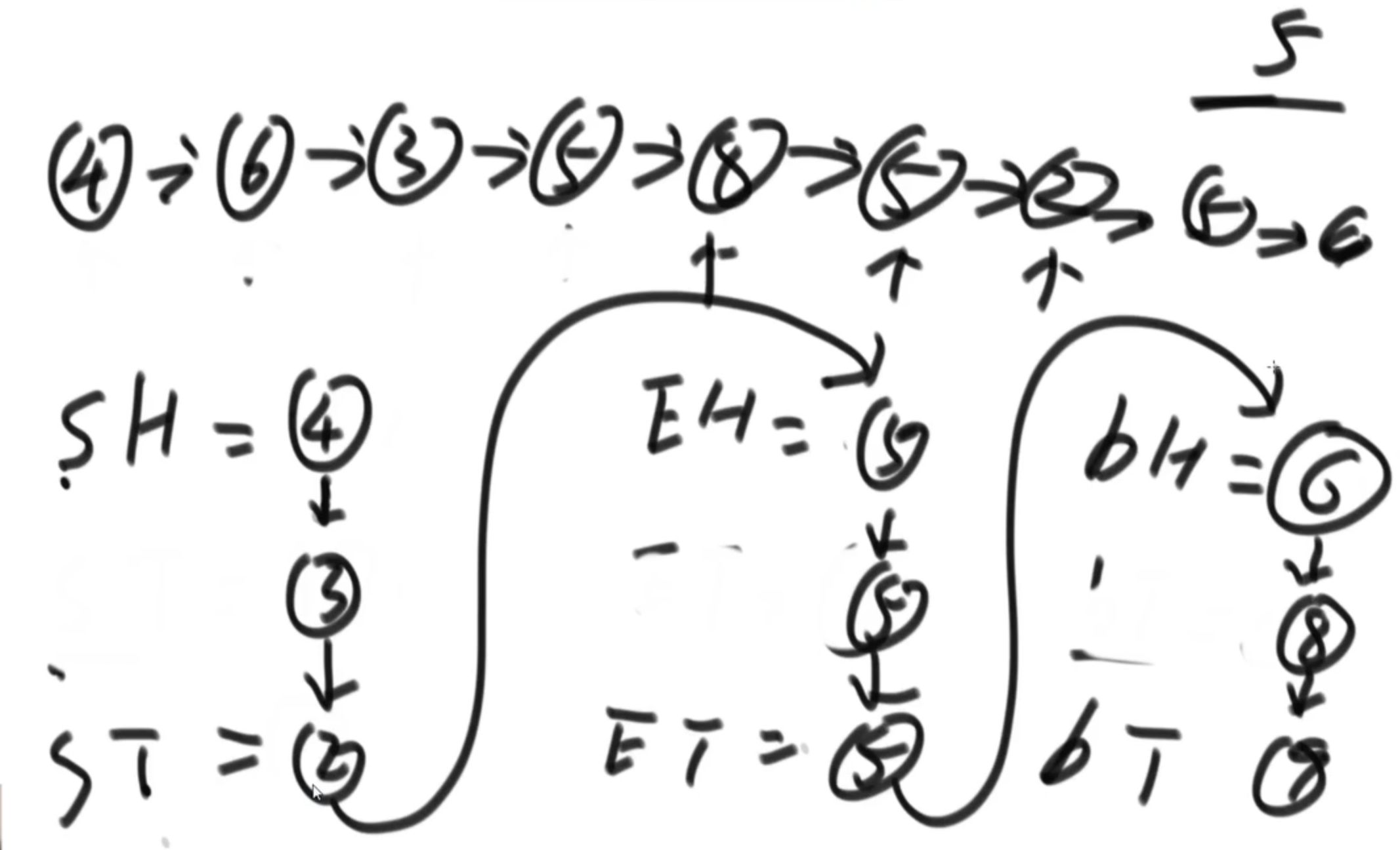
(1: 45: 00)
Hashtable
key (old Node) value (newly cloned Node)

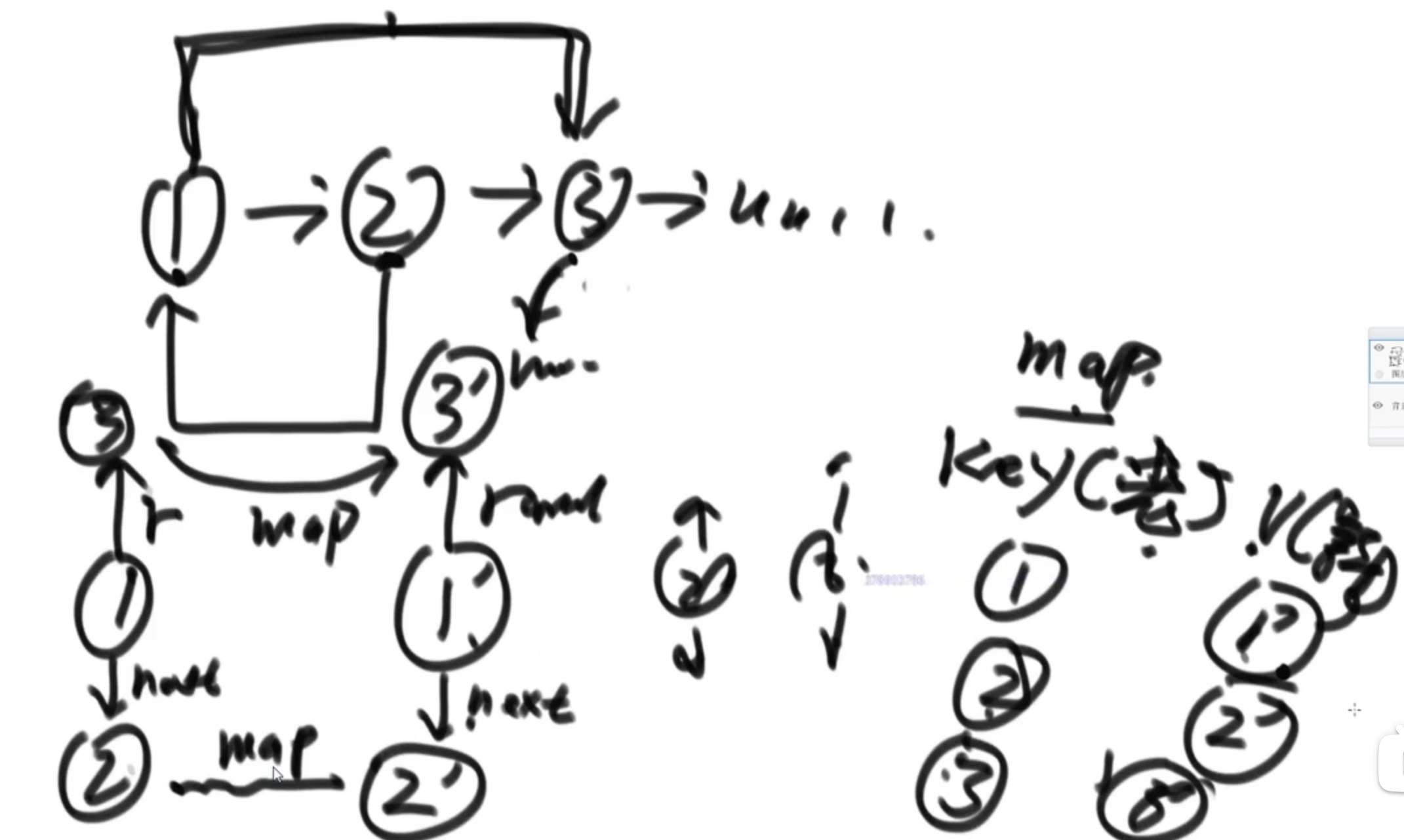
No hash table